轉自：https://blog.csdn.net/Ontheroad_/article/details/72739380

圖的儲存結構

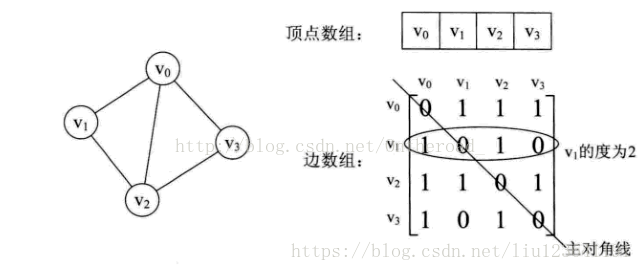
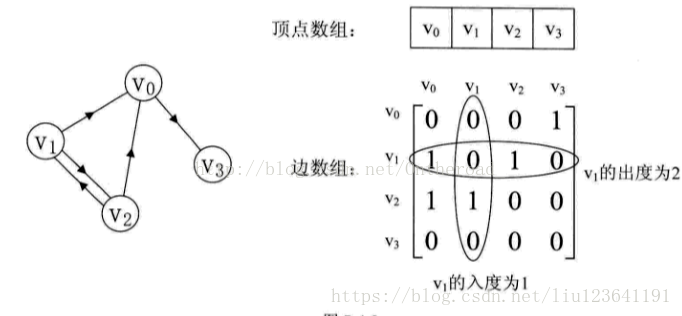
1.鄰接矩陣：兩個陣列，一個數組儲存“頂點集”，一個數組儲存“邊集”。

無向圖中：

有向圖中：

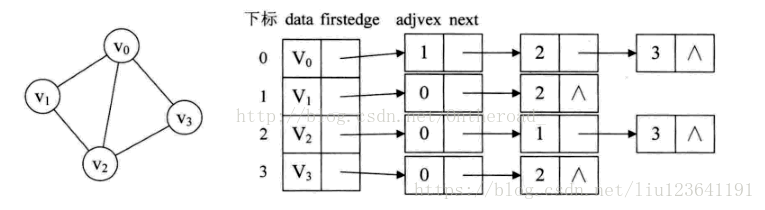
2.鄰接表：陣列與連結串列相結合的儲存方法。

對於帶權值的網圖，可以在邊表結點定義中再增加一個weight的資料域，儲存權值資訊即可。

圖的遍歷

1.深度優先遍歷（DFS）：類似於樹的先序遍歷（遞迴實現）。從圖中某個頂點v出發，訪問此頂點，然後從v的未被訪問的鄰接點出發深度優先遍歷圖，直至圖中所有和v有路徑想通的頂點都被訪問到。

    虛擬碼實現：

def depth_tree(tree_node):
    if tree_node is not None:
        print(tree_node._data)
        if tree_node._left is not None:
            return depth_tree(tree_node._left)
        if tree_node._right is not None:
            return depth_tree(tree_node._right)
 

2.廣度優先遍歷（BFS）：類似於樹的層次遍歷（佇列實現）。

    python程式碼實現：

def level_queue(root):
    if root is None:
        return
    my_queue = []
    node = root
    my_queue.append(node)
    while my_queue:
        node = my_queue.pop(0)
	print(node.elem)
	if node.lchild is not None:
	    my_queue.append(node.lchild)
	if node.rchild is not None:
	    my_queue.append(node.rchild)
 

最小生成樹

構造連通網的最小代價生成樹。

1.普里姆：先將一個起點加入最小生成樹，之後不斷尋找與最小生成樹相連的權值最小的邊能通向的點，並將其加入最小生成樹，直至所有頂點都在最小生成樹中。

2.克魯斯卡爾：在剩下的所有未選取的邊中，找最小邊，如果和已選取的邊構成迴路，則放棄，選取次小邊。

最短路徑

1.迪傑斯特拉演算法：把圖中的頂點集合V分成兩組，第一組為已求出最短路徑的頂點集合S（初始時S中只有源節點，以後每求得一條最短路徑，就將它對應的頂點加入到集合S中，直到全部頂點都加入到S中）；第二組是未確定最短路徑的頂點集合U。

2.弗洛伊德演算法：

（1）從任意一條單邊路徑開始。所有兩點之間的距離是邊的權，如果兩點之間沒有邊相連，則權為無窮大。

（2）對於每一對頂點u和v，看看是否存在一個頂點w使得從u到w再到v比已知的路徑更短。如果是，則更新它。