C++理解並實現堆排序
摘要
作為選擇排序的改進版,堆排序可以把每一趟元素的比較結果儲存下來,以便我們在選擇最小/大元素時對已經比較過的元素做出相應的調整。
堆排序是一種樹形選擇排序,在排序過程中可以把元素看成是一顆完全二叉樹,每個節點都大(小)於它的兩個子節點,當每個節點都大於等於它的兩個子節點時,就稱為大頂堆,也叫堆有序; 當每個節點都小於等於它的兩個子節點時,就稱為小頂堆。


(大頂堆(有序堆)) (小頂堆)
演算法思想(以大頂堆為例)
1.將長度為n的待排序的陣列進行堆有序化構造成一個大頂堆
2.將根節點與尾節點交換並輸出此時的尾節點
3.將剩餘的n -1個節點重新進行堆有序化
4.重複步驟2,步驟3直至構造成一個有序序列
假設待排序陣列為[20,50,10,30,70,20,80]
構造堆
在構造有序堆時,我們開始只需要掃描一半的元素(n/2-1 ~ 0)即可,為什麼?
因為(n/2-1)~0的節點才有子節點,如圖1,n=8,(n/2-1) = 3 即3 2 1 0這個四個節點才有子節點

(圖1:初始狀態)
所以程式碼4~6行for迴圈的作用就是將3 2 1 0這四個節點從下到上,從右到左的與它自己的子節點比較並調整最終形成大頂堆,過程如下:
第一次for迴圈將節點3和它的子節點7 8的元素進行比較,最大者作為父節點(即元素60作為父節點)
【紅色表示交換後的狀態】

第二次for迴圈將節點2和它的子節點5 6的元素進行比較,最大者為父節點(元素80作為父節點)

第三次for迴圈將節點1和它的子節點3 4的元素進行比較,最大者為父節點(元素70作為父節點)
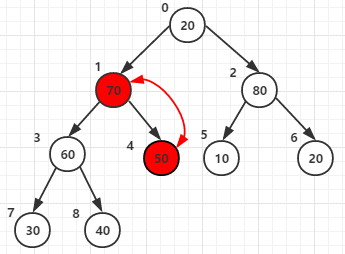
第四次for迴圈將節點0和它的子節點1 2的元素進行比較,最大者為父節點(元素80作為父節點)
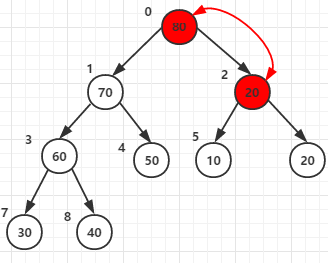
(注意這裡,元素20和元素80交換後,20所在的節點還有子節點,所以還要再和它的子節點5 6的元素進行比較,這就是28行程式碼 i = j
至此有序堆已經構造好了!如下圖:

調整堆
下面進行while迴圈
(1)堆頂元素80和尾40交換後-->調整堆
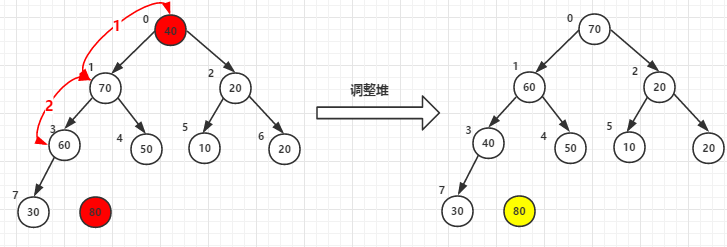
(2)堆頂元素70和尾30交換後-->調整堆
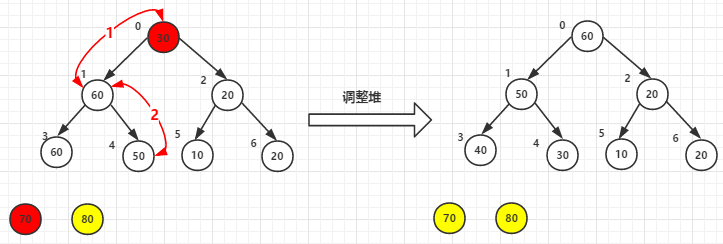
(3)堆頂元素60尾元素20交換後-->調整堆
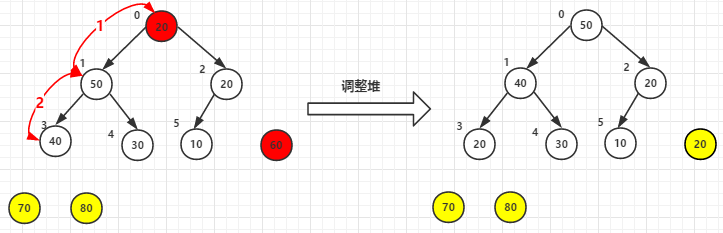
(4)其他依次類推,最終已排好序的元素如下:
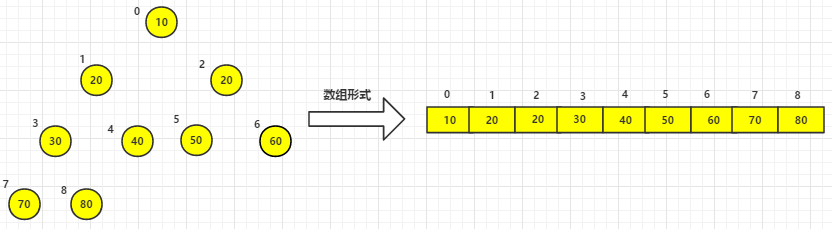
(5) 我們可以用一個動態圖來理解堆排序

(6) 排序演算法總結

堆排序是不穩定的排序演算法,不穩定發生在堆頂元素與A[i]交換的時刻。
比如序列:{ 9, 5, 7, 5 },堆頂元素是9,堆排序下一步將9和第二個5進行交換,得到序列 { 5, 5, 7, 9 },再進行堆調整得到{ 7, 5, 5, 9 },重複之前的操作最後得到{ 5, 5, 7, 9 }從而改變了兩個5的相對次序。
C++(STL程式碼)
#include<iostream>
#include<vector>
using namespace std;
/***************************************************************
本程式實現堆排序,堆排序是一種時間複雜度為
O(nlogn)的不穩定排序演算法,最好和最壞情況都
是O(nlogn),常用排序演算法連結:
https://www.cnblogs.com/eniac12/p/5329396.html
anthor:李金澤,BioInformation Lab,HIT 2018.11.01
*****************************************************************/
template<typename T>
void Swap(vector<T>& a, int i, int j) {
T temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
template<typename T>
void HeapSort(vector<T>& a) {
int len = a.size() - 1;
for (int i = len / 2 - 1; i >= 0; i--) {//構造一個大頂堆,這時的a[0]為最大值
AdjustHeap(a, i, len);
}
while (len >= 0) {
Swap(a, 0, len--);
AdjustHeap(a, 0, len);//調整堆,使其滿足堆的定義(父節點比它的倆子節點都要大)
}
}
template<typename T>
void AdjustHeap(vector<T>& a, int i, int len)
{
int left, right;//存放左右節點的下標
int MaxPoint;//存放較大子節點的下標
while ((left = 2 * i + 1) < len) {
right = left + 1;
MaxPoint = left;
if (left < len && a[right] > a[left]) {//當left==len時,i節點沒有右子節點,MaxPoint指標指向左節點
MaxPoint++;
}
if (a[i] < a[MaxPoint]) {
Swap(a, i, MaxPoint);
}
else { break; }
i = MaxPoint;//將父節點設定為子節點,開始向子樹調整堆結構
}
}
int main()
{
vector<int> a = { 20,50,20,40,70,10,80,30,60 };
cout << "排序之前:" << endl;
for (int i = 0; i < a.size(); i++) {
cout << a[i]<<" ";
}
HeapSort<int>(a);
cout << "排序之後:" << endl;
for (int i = 0; i < a.size(); i++) {
cout << a[i]<<" ";
}
getchar();
return 0;
}Java程式碼:
public class HeapSort {
private static void heapSort(int[] arr) {
int len = arr.length -1;
for(int i = len/2 - 1; i >=0; i --){ //堆構造
heapAdjust(arr,i,len);
}
while (len >=0){
swap(arr,0,len--); //將堆頂元素與尾節點交換後,長度減1,尾元素最大
heapAdjust(arr,0,len); //再次對堆進行調整
}
}
public static void heapAdjust(int[] arr,int i,int len){
int left,right,j ;
while((left = 2*i+1) <= len){ //判斷當前父節點有無左節點(即有無孩子節點,left為左節點)
right = left + 1; //右節點
j = left; //j"指標指向左節點"
if(j < len && arr[left] < arr[right]) //右節點大於左節點
j ++; //當前把"指標"指向右節點
if(arr[i] < arr[j]) //將父節點與孩子節點交換(如果上面if為真,則arr[j]為右節點,如果為假arr[j]則為左節點)
swap(arr,i,j);
else //說明比孩子節點都大,直接跳出迴圈語句
break;
i = j;
}
}
public static void swap(int[] arr,int i,int len){
int temp = arr[i];
arr[i] = arr[len];
arr[len] = temp;
}
public static void main(String[] args) {
int array[] = {20,50,20,40,70,10,80,30,60};
System.out.println("排序之前:");
for(int element : array){
System.out.print(element+" ");
}
heapSort(array);
System.out.println("\n排序之後:");
for(int element : array){
System.out.print(element+" ");
}
}
}