常微分方程1:與方程聯系的相流
阿新 • • 發佈:2017-07-28
方法 option 一點 display 是否 http tle 位置 title 1.1 向量場
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
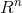 中一開集
中一開集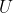 上的向量場
上的向量場) 指的是
指的是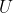 上的一個
上的一個![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 向量值函數:
向量值函數:![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
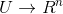 1.2 常微分方程
1.2 常微分方程
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
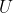 上的常微分方程指的是形如 :
上的常微分方程指的是形如 :
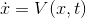
) 的方程,其中
的方程,其中) 是定義在
是定義在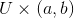 上的向量場.若有
上的向量場.若有) 是定義在
是定義在) 中某個開集
中某個開集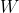 上的向量值函數使上述方程成立,則稱
上的向量值函數使上述方程成立,則稱) 是該方程在
是該方程在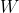 上的解。
1.3 右端自治情況下的意義
若
上的解。
1.3 右端自治情況下的意義
若=V(x)) 與
與 無關,則方程
無關,則方程) 的意思是:
是否存在這樣的曲線
的意思是:
是否存在這樣的曲線) ,使它在每一點處的切向量正好是給定的向量場在這一點處的取值?
從運動學角度來看,如果左端和右端都是一維的情形,方程的意思是,是否存在
,使它在每一點處的切向量正好是給定的向量場在這一點處的取值?
從運動學角度來看,如果左端和右端都是一維的情形,方程的意思是,是否存在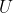 上的這樣一種運動,使得在每一點的運動速度是給定的數值?
右端與t無關的情形,稱方程是一個自治系統,否則是非自治的。
上的這樣一種運動,使得在每一點的運動速度是給定的數值?
右端與t無關的情形,稱方程是一個自治系統,否則是非自治的。 ![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
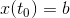
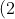) 的限制條件。它指的是曲線或者運動在某一刻的位置,常常取
的限制條件。它指的是曲線或者運動在某一刻的位置,常常取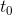
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() =0,表示初始時刻的運動狀態。
顯然我們會碰到這樣的問題:
1.方程是否存在滿足
=0,表示初始時刻的運動狀態。
顯然我們會碰到這樣的問題:
1.方程是否存在滿足) 和
和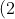) 在
在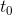
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 附近的一個解?
2.這個解是否在其存在區間上是唯一的?
3.這個解能在多大的範圍內存在?
我們可以先看兩個例子:
1.
附近的一個解?
2.這個解是否在其存在區間上是唯一的?
3.這個解能在多大的範圍內存在?
我們可以先看兩個例子:
1.![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
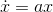
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
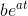 是方程的解,並且它在整個區間上存在。它實際上是唯一的解(初等積分法可以求出)
2.
是方程的解,並且它在整個區間上存在。它實際上是唯一的解(初等積分法可以求出)
2.![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()

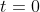 附近存在唯一解
附近存在唯一解
=-1/(t-1)) 註意到解不能延拓到1的右側,所以該方程的解的存在區間是有限的。
1.5 微分同胚
註意到解不能延拓到1的右側,所以該方程的解的存在區間是有限的。
1.5 微分同胚 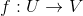
 和
和![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
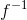 都是
都是![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 光滑映射。
微分同胚的存在性必然表明
光滑映射。
微分同胚的存在性必然表明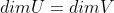 .或者說,維數是微分同胚意義下的不變量.
1.6 相流
相流
.或者說,維數是微分同胚意義下的不變量.
1.6 相流
相流![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 是
是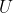 上的一族自微分同胚
上的一族自微分同胚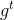 ,滿足以下兩個條件:
1.
,滿足以下兩個條件:
1.![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
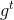 是自微分同胚族,
是自微分同胚族, 2.(群條件)
2.(群條件) ![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()

![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 均在整個實軸上存在唯一的解,則這樣的自治方程可以確定相流.
定義
均在整個實軸上存在唯一的解,則這樣的自治方程可以確定相流.
定義![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() :
:
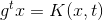 其中
其中) 是自治方程在初始條件
是自治方程在初始條件
=x) 的解在時刻
的解在時刻 時的位置。
定理1.7.1
1.由上述方法確定
時的位置。
定理1.7.1
1.由上述方法確定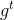 的
的![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 是微分同胚
2.
是微分同胚
2.![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]()
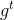 是一族相流.
註意到
是一族相流.
註意到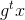 是方程在初始條件
是方程在初始條件
=x) 下的解。
下的解。![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 它是無限延伸的曲線,稱為過
它是無限延伸的曲線,稱為過
) 是自治方程的解,則
是自治方程的解,則) 同樣是方程的解.
而1我們目前還沒法證明
同樣是方程的解.
而1我們目前還沒法證明![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 的可微性,這實際上是解對初值條件的可微依賴性,我們先假定自治方程滿足大範圍存在性和整體唯一性的時候是成立的。過後我們會用常微分方程基本定理來證明它。
1.8 相流決定的向量場
給定
的可微性,這實際上是解對初值條件的可微依賴性,我們先假定自治方程滿足大範圍存在性和整體唯一性的時候是成立的。過後我們會用常微分方程基本定理來證明它。
1.8 相流決定的向量場
給定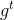
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() ,考慮
,考慮
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program. 技術分享]() 右側是在零時刻求的導數。它得到了
右側是在零時刻求的導數。它得到了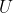 上的一個向量場。
1.9 相流,向量場和自治方程的關系
思考以下三句話:
1.相流可以確定向量場(在1.8的意義下)
2.向量場可以得到自治方程
3.特殊的自治方程可以得到相流
上的一個向量場。
1.9 相流,向量場和自治方程的關系
思考以下三句話:
1.相流可以確定向量場(在1.8的意義下)
2.向量場可以得到自治方程
3.特殊的自治方程可以得到相流
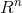 中一開集
中一開集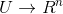 1.2 常微分方程
1.2 常微分方程
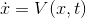
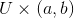 上的向量場.若有
上的向量場.若有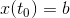
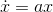
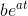 是方程的解,並且它在整個區間上存在。它實際上是唯一的解(初等積分法可以求出)
2.
是方程的解,並且它在整個區間上存在。它實際上是唯一的解(初等積分法可以求出)
2.
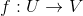
是微分同胚,如果
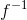 都是
都是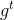 ,滿足以下兩個條件:
1.
,滿足以下兩個條件:
1.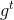 是自微分同胚族,
是自微分同胚族, 2.(群條件)
2.(群條件) 
1.7 由特殊的自治方程所決定的相流 若自治方程在初始條件下
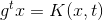 其中
其中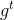 的
的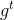 是一族相流.
註意到
是一族相流.
註意到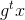 是方程在初始條件
是方程在初始條件
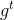
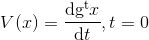
常微分方程1:與方程聯系的相流
