機器學習第十篇——尋找獨立特徵
尋找獨立特徵
如何在資料集並未明確標識結果的前提下,從中提取出重要的潛在特徵來,和聚類一樣,這些方法的目的不是為了預測,而是要嘗試對資料進行特徵識別,並且告訴我們值得關注的重要資訊
尋找獨立特徵應用:
*雞尾酒宴會 ?????????????????
*對重複出現於一組文件中的單詞使用模式(word-usage-patterns)進行識別,可以有效識別出以不同組合形式獨立出現於各個文件中的主題
非負矩陣因式分解(NMF)
當前:一個帶單詞計數資訊的文章矩陣
| hurricane | democrats | florida | elections | |
| hurricane | 20 | 2 | 30 | 0 |
| Democrats sweep elections | 0 | 16 | 1 | 9 |
| Democrats dispute Florida ballots | 0 | 10 | 6 | 11 |
目標:對其進行因式分解,即:找到兩個更小的矩陣,使得二者相乘以得到原來的矩陣。這兩個矩陣分別是特徵矩陣和權重矩陣。權重矩陣*特徵矩陣=文章矩陣
權重矩陣
| 特徵1 | 特徵2 | 特徵3 | |
| hurricane | 10 | 0 | 0 |
| Democrats sweep elections | 0 | 8 | 1 |
| Democrats dispute Florida ballots | 0 | 5 | 6 |
特徵矩陣
| hurricane | democrats | florida | elections | |
| 特徵1 | 2 | 0 | 3 | 0 |
| 特徵2 | 0 | 2 | 0 | `1 |
| 特徵3 | 0 | 0 | 1 | 1 |
如果特徵數量與文章數量恰好相等,那麼最理想的結果就是能夠為每一篇文章都找到一個與之完美匹配的特徵。
使用矩陣因式分解的目的,是為了縮減觀測資料的集合規模,並且保證縮減之後足以反映某些共性特徵。理想情況下,這個相對較小的特徵集合能夠與不同的權重值相結合,從而完美地重新構造出原始的資料集,但在現實中這種可能性是非常小的,因此,演算法的目標是要儘可能地重新構造出原始資料集來。
矩陣因式分解演算法實現
前提:
numpy安裝 使用 python -m pip install numpy 命令
新建nmf.py
from numpy import *
import numpy as np
#針對兩個同樣大小的矩陣遍歷其中的每一個值
#並將兩者之間差值的平方累加起來
def difcost(a, b):
dif = 0
# 遍歷矩陣中的每一行和每一列
for i in range(shape(a)[0]):
for j in range(shape(a)[1]):
# 將差值相加
dif += pow(a[i, j] - b[i, j], 2)
return dif現在,需要一種方法能夠逐步地更新矩陣,以使成本函式的計算值逐步降低。模擬退火,遺傳演算法,乘法更新法則(multiplicative update rules)
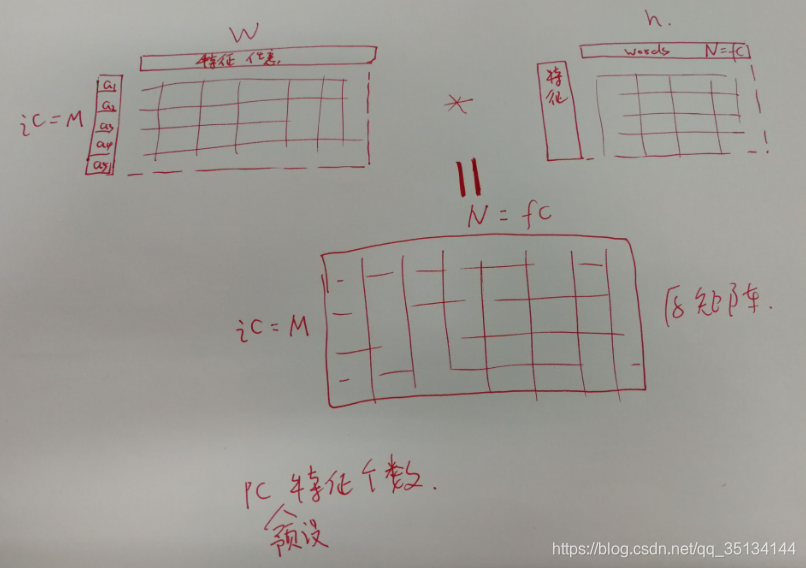
| hn | 經轉置後的權重矩陣與資料矩陣相乘得到的矩陣 |
| hd | 經轉置後的權重矩陣與原權重矩陣相乘,再與特徵矩陣相乘得到的矩陣 |
| wn | 資料矩陣與經轉置後的特徵矩陣相乘得到的矩陣 |
| wd | 權重矩陣與特徵矩陣相乘,再與經轉置後的特徵矩陣相乘得到的矩陣 |
| pc | 特徵個數 |
def factorize(v, pc=10, iter=50):
ic = shape(v)[0] #行數
fc = shape(v)[1] #列數
# 以隨機值初始化權重矩陣和特徵矩陣
w = matrix([[random.random() for i in range(pc)] for i in range(ic)])
h = matrix([[random.random() for i in range(fc)] for i in range(pc)])
# 最多執行Iter次操作
for i in range(iter):
wh = w * h
# 計算當前差值
cost = difcost(v, wh)
print(cost)
#if i % 10 == 0:
# 如果矩陣已分解徹底,則立即終止
if cost == 0: break
# 更新特徵矩陣 ………………………………………………………………………………………………………………………………………………………………
hn = (transpose(w) * v)
hd = (transpose(w) * w * h)
h = matrix(np.array(h) * np.array(hn) / np.array(hd))
# 更新權重矩陣 ………………………………………………………………………………………………………………………………………………………………
wn = (v * transpose(h))
wd = (w * h * transpose(h))
w = matrix(np.array(w) * np.array(wn) / np.array(wd))
return w, h文章矩陣構造
import feedparser
import re
from numpy import *
import nmf
feedlist = ['http://www.shoemoney.com/feed/']
def separatewords(text):
splitter = re.compile('\\W*')
return [s.lower() for s in splitter.split(text) if len(s) > 3]
def getarticlewords():
allwords = {}
articlewords = []
articletitles = []
ec = 0
# 遍歷每個訂閱源
for feed in feedlist:
f = feedparser.parse(feed)
# print('f: ', f)
# 遍歷每篇文章
for e in f.entries:
# 跳過標題相同的文章
if e.title in articletitles: continue
# print('title: ', e.title)
# print('description: ', e.description)
# 提取單詞
txt = e.title + e.description
# print('txt: ',txt)
words = separatewords(txt)
# print('words: ', words)
articlewords.append({})
articletitles.append(e.title)
# 在allwords和articlewords中增加針對當前單詞的計數
for word in words:
allwords.setdefault(word, 0)
allwords[word] += 1
articlewords[ec].setdefault(word, 0)
articlewords[ec][word] += 1
ec += 1
return allwords, articlewords, articletitles
allw, artw, artt = getarticlewords()def outfile():
out = open('data.excel', 'w')
out.write('Article')
for word in allw: out.write('\t%s' % word)
out.write('\n')
i = 0
for arti in artt:
out.write(arti)
for j in allw.keys():
# print('j: ',j)
if j in artw[i].keys():
out.write('\t%d' % artw[i][j])
else:
out.write('\t0')
i += 1
out.write('\n')data.excel :
def makematrix(allw, articlew):
wordvec = []
# 只考慮那些普通的但又不至於非常普通的單詞
for w, c in allw.items():
if c > 3 and c < len(articlew) * 0.6:
wordvec.append(w)
# 構造單詞矩陣
l1 = [[(word in f and f[word] or 0) \
for word in wordvec] for f in articlew]
return l1, wordvecdef showfeatures(w, h, titles, wordvec, out='features.txt'):
outfile = open(out, 'w')
pc, wc = shape(h)
toppatterns = [[] for i in range(len(titles))]
patternnames = []
# 遍歷所有特徵
for i in range(pc):
slist = []
# 構造一個包含單詞及其權重資料的列表
for j in range(wc):
slist.append((h[i, j], wordvec[j]))
# 將單詞列表倒序排列
#print('slist: ',slist)
slist.sort()
#print('slist.sort: ',slist)
slist.reverse()
#print('slist.reverse: ', slist)
# 列印開始的6個元素
n = [s[1] for s in slist[0:6]]
#print('n: ',n)
outfile.write(str(n) + '\n')
patternnames.append(n)
# 構造一個針對該特徵的文章列表
flist = []
for j in range(len(titles)):
# 加入文章及其權重資料
flist.append((w[j, i], titles[j]))
toppatterns[j].append((w[j, i], i, titles[j]))
# 將該列表倒序排列
flist.sort()
flist.reverse()
# 顯示前3篇文章
for f in flist[0:3]:
outfile.write(str(f) + '\n')
outfile.write('\n')
outfile.close()
# 返回模式名稱,以供後續使用
return toppatterns, patternnamesresult :

def showarticles(titles, toppatterns, patternnames, out='articles.txt'):
outfile = open(out, 'w')
# 遍歷所有的文章
for j in range(len(titles)):
outfile.write(titles[j] + '\n')
# 針對該篇文章,獲得排位最靠前的幾個特徵
# 並將其按倒序排列
toppatterns[j].sort()
toppatterns[j].reverse()
# 列印前3個模式
for i in range(3):
outfile.write(str(toppatterns[j][i][0]) + ' ' + \
str(patternnames[toppatterns[j][i][1]]) + '\n')
outfile.write('\n')
outfile.close()result :

提取效果還可以。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
利用股票市場資料
對於某支股票而言,成交量就是指在某一給定時間段內(通常是一天)所買賣的股票份數。通過對交易量資料的分析,可以找出反映重要交易日的模式,以及潛在因素如何得以驅動多支股票交易量的原因。
當股票價格有較大變化的時候,成交量在那幾天往往就會變得很高,這通常會發生在公司發表重要聖母或釋出財務報告的時候。此外,當有涉及公司或業界的新聞報道時,也會導致價格出現‘突變’(spikes)。在缺少外部事件影響的情況下,對於某支股票而言,成交量通常是保持不變的。
之所以選擇成交量而不是收盤價作為考查物件,是因為NMF試圖尋找的特徵是可以相加在一起的正數,價格通常會受事件的影響而向下走,成交量更容易建模,它有一個可以受外部影響而遞增的基準水平。
沒有資料!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
?????????????????????????????????????????

import nmf
import urllib
from numpy import *
tickers = ['YHOO', 'AVP', 'BIIB', 'BP', 'CL', 'CVX',
'DNA', 'EXPE', 'GOOG', 'PG', 'XOM', 'AMGN']
shortest = 300
prices = {}
dates = None
for t in tickers:
# 開啟url
rows = urllib.request.urlopen('http://ichart.finance.yahoo.com/table.csv?' + \
's=%s&d=11&e=26&f=2006&g=d&a=3&b=12&c=1996' % t + \
'&ignore=.csv').readlines()
# 從每一行中提取成交量
# strip()移除字串頭尾指定的字元(預設為空格或換行符)
prices[t] = [float(r.split(',')[5]) for r in rows[1:] if r.strip() != '']
if len(prices[t]) < shortest: shortest = len(prices[t])
if not dates:
dates = [r.split(',')[0] for r in rows[1:] if r.strip() != '']
l1 = [[prices[tickers[i]][j] for i in range(len(tickers))]
for j in range(shortest)]
w,h=nmf.factorize(matrix(l1),pc=5)
print('特徵: ',h)
print('權重: ',w)《集體智慧》書時間太長了,很多東西都用不了了。。。。。。。。。。。。。。。。。
?????????????????????????????????????????
結果顯示
#遍歷所有特徵
for i in range(shape(h)[0]):
print('Feature %d' % i)
#得到最符合當前特徵的股票
ol=[(h[i,j],tickers[j]) for j in range(shape(h)[1])]
ol.sort()
ol.reverse()
for j in range(12):
print(ol[j])
print()
#顯示最符合當前特徵的交易日期
porder=[(w[d,i],d) for d in range(300)]
porder.sort()
porder.reverse()
print([(p[0],dates[p[1]]) for p in porder[0:3]])
print()?????????????????????????????????????????
