構造價格模型

在利用多種不同屬性（比如價格）對數值型資料進行預測時，貝葉斯分類器、決策樹、支援向量機都不是最佳的演算法。

本篇將對一系列演算法進行考查，這些演算法可以接受訓練，根據之前見過的樣本資料作出資料類的預測，而且它們還可以顯示出預測的概率分佈情況，以幫助使用者對預測過程加以解釋。後續部分將考查如何利用這些演算法來構造價格預測模型。

進行數值預測的一項關鍵工作是確定哪些變數是重要的。

構造一個樣本資料集

根據一個人為假設的簡單模型來構造一個有關葡萄酒價格的資料集。酒的價格是根據酒的等級及其儲藏的年代來共同決定的。該模型假設葡萄酒有‘峰值年’的現象，即：較之峰值年而言，年代稍早一些的酒的品質會比較好一些，而緊隨其後的品質則稍差些

def wineprice(rating,age):
    peak_age=rating-50

    #根據等級來計算價格
    price=rating/2
    if age>peak_age:
        #經過‘峰值年’，後繼5年裡其品質將會變差
        price=price*(5-(age-peak_age))
    else:
        #價格在接近‘峰值年’時會增加到原值的5倍
        price=price*(5*((age+1)/peak_age))
    if price<0: price=0
    return price
 

'''
構造表示葡萄酒價格的資料集，
並在原有價格的基礎上通過‘噪聲’隨機地加減了20%，
以此來表現諸如稅收和價格區域性變動的情況
'''

def wineset1():
    rows=[]
    for i in range(300):
        #隨機生成年代和等級
        rating=random()*50+50
        age=random()*50

        #得到一個參考價格
        price=wineprice(rating,age)
        #增加‘噪聲’    ##########################################################
        price*=(random()*0.4+0.8)
        #加入資料集
        rows.append({'input':(rating,age),'result':price})
    return rows
 

K-最鄰近演算法（kNN）

通過尋找與當前所關注的商品情況相似的一組商品，對這些商品的價格求均值，進而作出價格預測，k指的是為了求得最終結果而參與求平均值運算的商品數量。

鄰近數

過少過多均不好

定義相似度

尋找一種衡量兩件商品之間相似程度的方法。

補充：歐幾里得距離演算法

#歐幾里得距離演算法
def euclidean(v1,v2):
    d=0.0
    for i in range(len(v1)):
        d+=(v1[i]-v2[i])**2
    return math.sqrt(d)

k-最鄰近演算法

優點：1、每次有新資料加入時，都無需重新進行訓練

缺點：1、計算量大    2、該函式在計算距離是對年代和等級是同等看待的，但現實是，某些變數對最終價格所產生的影響往往比其他變數更大

def getdistance(data,vec1):
    distancelist=[]
    for i in range(len(data)):
        vec2=data[i]['input']
        distancelist.append((euclidean(vec1,vec2),i))
    distancelist.sort()
    return distancelist

def knnestimate(data,vec1,k=5):
    #得到經過排序的距離值
    dlist=getdistance(data,vec1)
    avg=0.0

    #對前k項結果求平均
    for i in range(k):
        idx=dlist[i][1]
        avg+=data[idx]['result']
    avg=avg/k
    return avg

print(knnestimate(data,(95.0,3.0)))
print(knnestimate(data,(99.0,3.0)))
print(wineprice(95.0,5.0))
print(wineprice(99.0,3.0))
print("***kNN")
print(knnestimate(data,(99.0,5.0)))
print("***真實")
print(wineprice(99.0,5.0))#得到實際價格
print("***少")
print(knnestimate(data,(99.0,5.0),k=1)) #嘗試更少的近鄰
print("***多")
print(knnestimate(data,(99.0,5.0),k=10)) #嘗試更少的近鄰

為鄰近分配權重

反函式

該函式最為簡單的一種形式是返回距離的倒數，不過有時候，完全一樣或非常接近的商品，會使權重值變得非常之大，甚至是無窮大，基於這樣的原因，有必要在對距離求倒數之前先加上一個小小的常量

def inverseweight(dist,num=1.0,const=0.1):
    return num/(dist+const)

缺陷在於它會為近鄰項賦以很大的權重，而稍遠一點的項，其權重則會‘衰減’得很快。這種情況也許正是我們所期望的，但有的時候，這也會使演算法對噪聲變的更加敏感。

減法函式

def subtractweight(dist,const=1.0):
    if dist>const:
        return 0
    else:
        return const-dist

該函式克服了反函式對近鄰項權重分配過大的潛在問題，但是由於權重值最終會跌至0，因此，我們有可能找不到距離足夠近的項，將其視作近鄰，即：對於某些項，演算法根本就無法作出預測。

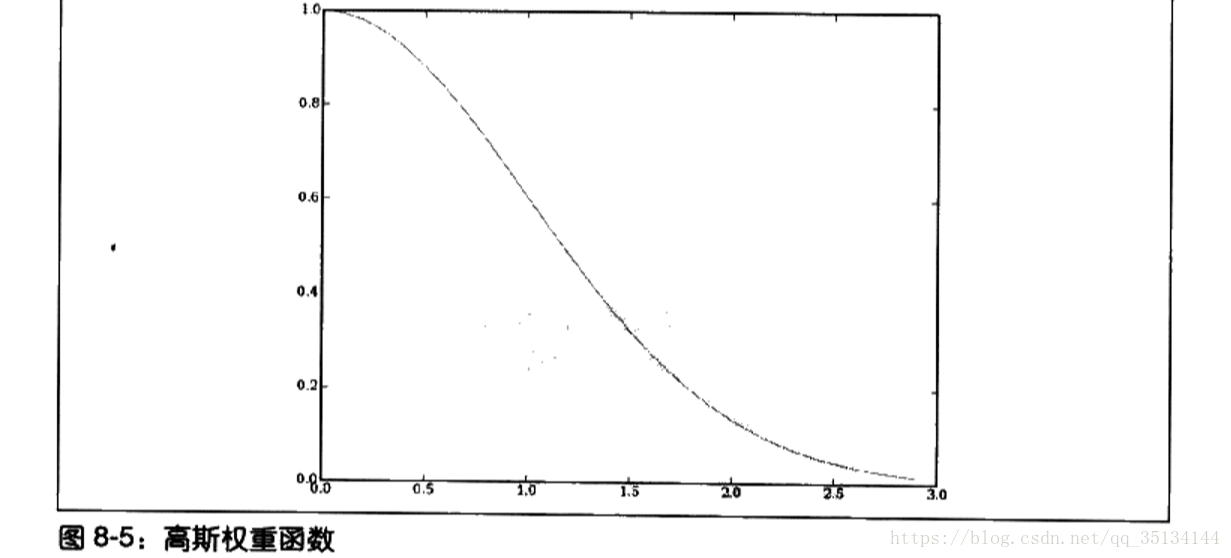
高斯函式

‘鍾型曲線’

#高斯函式
def gaussian(dist,sigma=10.0):
    return math.e**(-dist**2/(2*sigma**2))

加權KNN

#加權KNN
def weightedknn(data,vec1,k=5,weightf=gaussian):
    #得到距離值
    dlist=getdistances(data,vec1)
    avg=0.0
    totalweight=0.0

    #得到加權平均值
    for i in range(k):
        dist=dlist[i][0]
        idx=dlist[i][1]
        weight=weightf(dist)
        avg+=weight*data[idx]['result']
        totalweight+=weight
    avg=avg/totalweight
    return avg

交叉驗證 

def dividedata(data,test=0.05):
    trainset=[]
    testset=[]
    for row in data:
        if random()<test:
            testset.append(row)
        else:
            trainset.append(row)
    return trainset,testset

def testalgorithm(algf,trainset,testset):
    error=0.0
    for row in testset:
        guess=algf(trainset,row['input'])
        error+=(row['result']-guess)**2
    return error/len(testset)

def crossvalidate(algf,data,trials=100,test=0.05):
    error=0.0
    for i in range(trials):
        trainset,testset=dividedata(data,test)
        error+=testalgorithm(algf,trainset,testset)
    return error/trials



def knn3(d,v):
    return knnestimate(d,v,k=3)

def knn1(d,v):
    return knnestimate(d,v,k=1)

選擇太少或太多的近鄰都會導致效果不佳。

加權kNN演算法似乎能夠針對上述資料給出更好的結果。

對於一個特定的訓練集而言，選擇引數只須做一次即可，但隨著訓練集內容的增長，偶爾還須對其進行再次的更新。 

不同型別的變數

def wineset2():
    rows=[]
    for i in range(300):
        #隨機生成年代和等級
        rating=random()*50+50
        age=random()*50

        aisle=float(randint(1,20))
        bottlesize=[375.0,750.0,1500.0,3000.0][randint(0,3)]
        #得到一個參考價格
        price=wineprice(rating,age)
        price*=(bottlesize/750)
        #增加‘噪聲’    ##########################################################
        price*=(random()*0.2+0.9)
        #加入資料集
        rows.append({'input':(rating,age,aisle,bottlesize),'result':price})
    return rows

即使資料集現在包含了更多的資訊，而且噪聲也比以前更少了，但是crossvalidate函式實際返回的結果較之以前卻更為糟糕。其原因在於，演算法現在還不知道如何對不同的變數加以區別對待。

因為之前的兩個變數都位於同一值域範圍內，因此，利用這些變數一次性算出距離值是有意義的。

酒瓶尺寸和原先的變數相比，對距離計算所產生的影響更為顯著——其影響將超過任何其他變數對距離計算所構成的影響，這意味著，在計算距離的過程中其他變數根本就未被考慮在內。除此之外，還可能會遇到的另一個問題是資料集中引入了完全不相關的變數，如安放葡萄酒的通道號。

按比例縮放

def rescale(data, scale):
    scaleddata = []
    for row in data:
        scaled = [scale[i] * row['input'][i] for i in range(len(scale))]
        scaleddata.append({'input': scaled, 'result': row['result']})
    return scaleddata

對縮放結果進行優化

大多數時候我們所面對的資料集都不是自己構造的，而且我們也未必知道，到底哪些變數是不重要的，而哪些變數又對計算結果有著重大的影響。理論上我們可以嘗試大量不同的組合，直到發現一個足夠好的結果為止，不過也許有數以百計的變數須要考查，並且這項工作可能會非常地乏味。

def createcostfunction(algf,data):
    def costf(scale):
        sdata=rescale(data,scale)
        return crossvalidate(algf,sdata,trials=10)
    return costf

weightdomain=[(0,20)]*4

from optimization import annealingoptimize,geneticoptimize
data = wineset2()
costf=createcostfunction(knnestimate,data)
print(annealingoptimize(weightdomain,costf,step=5))
print(geneticoptimize(weightdomain,costf,popsize=50,step=1,mutprob=0.2,elite=0.2,maxiter=100))

實驗做的有問題。。。。。。。。。 

利用模擬退火以及遺傳演算法等優化演算法地一個好處在於，我們很快就能發覺哪些變數是重要地，並且其重要程度有多大。

不對稱分佈 

若葡萄酒購買者分別來自兩個彼此獨立的群組：一部分人是從小酒館購得的葡萄酒，而另一部分人則是從折扣店購得，並且後者得到了50%的折扣。

def wineset3():
    rows=wineset1()
    for row in rows:
        if random()<0.5:
            #葡萄酒是從折扣店購得的
            row['result']*=0.5
    return rows

演算法給出的評價值將同時涉及兩組人群，這就相當於可能有25%的折扣。為了不只是簡單地得到一個平均值，則需要一種方法能夠在某些方面更近一步地對資料進行考查。

估計概率密度

假設輸入條件為99%和20年，那麼我們需要一個函式來告訴我們，價格介於40美元和80美元之間的機率是50%，而價格介於80美元和100美元之間的機率也是50%。

函式首先計算位於該範圍內近鄰的權重值，然後計算所有近鄰的權重值，最終的概率等於在指定範圍內的近鄰權重之和除以所有權重之和。

def probguess(data,vec1,low,high,k=5,weightf=gaussian):
    dlist=getdistances(data,vec1)
    nweight=0.0
    tweight=0.0

    for i in range(k):
        dist=dlist[i][0]
        idx=dlist[i][1]
        weight=weightf(dist)
        v=data[idx]['result']

        #當前資料點位於指定範圍內嗎？
        if v>=low and v<=high:
            nweight+=weight
        tweight+=weight
    if tweight==0 : return 0

    #概率等於位於指定範圍內的權重值除以所有權重值
    return nweight/tweight

 繪製概率分佈

第一種方法：累計概率分佈

圖形從概率為0開始，爾後隨著商品在某一價位出命中的概率值而逐級遞增。直至最高位處，圖形對應的概率值達到1

#繪製概率分佈
from pylab import *
# a=array([1,2,3,4])
# b=array([4,2,3,1])
# plot(a,b)
# show()
# t1=arange(0.0,10.0,0.1)
# plot(t1,sin(t1))
# show()
#累積概率
def cumulativegraph(data,vec1,high,k=5,weightf=gaussian):
    t1=arange(0.0,high,0.1)
    cprob=array([probguess(data,vec1,0,v,k,weightf) for v in t1])
    plot(t1,cprob)
    show()

第二種：假設每個位點的概率都等於其周邊概率的一個加權平均

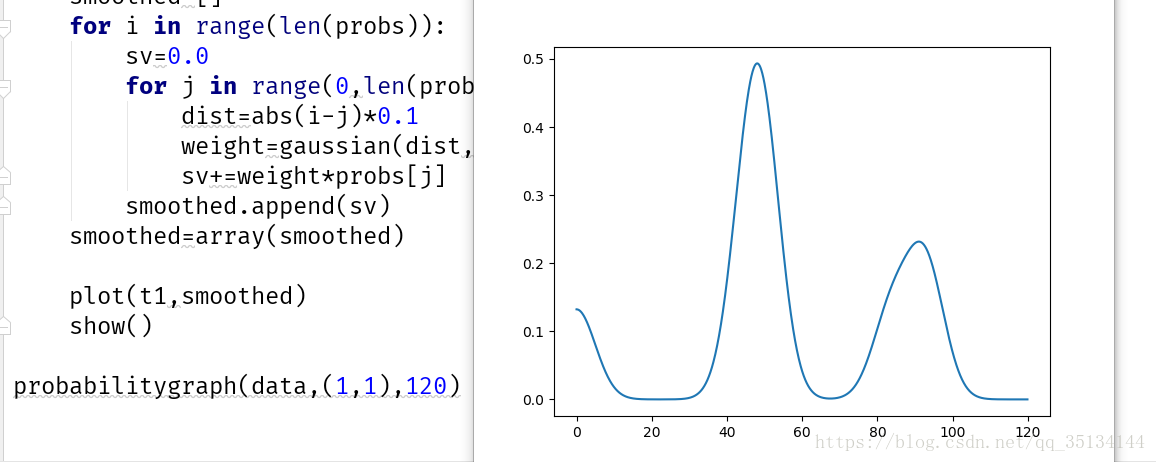
def probabilitygraph(data,vec1,high,k=5,weightf=gaussian,ss=5.0):
    #建立一個代表價格的值域範圍
    t1=arange(0.0,high,0.1)

    #得到整個值域範圍內的所有概率
    probs=[probguess(data,vec1,v,v+0.1,k,weightf) for v in t1]

    #通過加上近鄰概率的高斯計算結果，對概率值做平滑處理
    smoothed=[]
    for i in range(len(probs)):
        sv=0.0
        for j in range(0,len(probs)):
            dist=abs(i-j)*0.1
            weight=gaussian(dist,sigma=ss)
            sv+=weight*probs[j]
        smoothed.append(sv)
    smoothed=array(smoothed)

    plot(t1,smoothed)
    show()