在介紹條件隨機場之前，先介紹和條件隨機場緊密相關的馬爾可夫性。 全域性馬爾可夫性：給定兩個變數子集的分離集，則這兩個變數子集條件獨立。 也就是說 A和B在給定C的條件下獨立。

由全域性馬爾可夫性可以得到兩個有用的推論 區域性馬爾可夫性： 也就是說給定某變數的臨接變數，則該變數條件獨立於其他變數。

成對馬爾科夫性： 給定所有其他變數，兩個非鄰接變數條件獨立。 在馬爾可夫隨機場中，多個變數之間的聯合概率分佈能基於團分解為多個因子的乘積，每個因子僅與一個團相關。具體團分解可以參照西瓜書。那麼聯合概率可以表示為勢函式的乘積。如下圖所示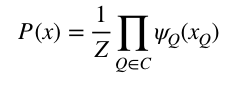： 勢函式的作用是刻畫變數集x中變數之間的相關關係，它應該是非負函式，為了滿足於非負性，指數函式常被用來定義勢函式。 條件隨機場試圖對多個變數在給定觀測值後對條件概率進行建模。 若令x

y可以結構性變數，也就是y的變數之間可以具有相關性。 只要每個變數y都具有馬爾可夫性，則（y，x）構成一個條件隨機場。

條件隨機場使用勢函式和圖結構上的團來定義條件概率P（y|x）

其中有用於定義在觀測序列的兩個相鄰標記位置上的轉移特徵函式，用於刻畫相鄰標記變數之間的相關關係以及觀測序列對他們的影響。 也有用於定義觀測序列對標記變數影響的相關函式。

假設已經觀察到的變數為X，Z表示為隱變數，若欲對引數做極大似然估計，則應最大化對數似然。然而因為Z是隱變數，無法直接求解，於是可以通過對Z計算期望來最大化已經觀測資料的對數邊際似然。

EM演算法，期望最大化演算法，是常用的估計引數隱變數的工具。若模型引數已知，就可以推斷隱變數Z的期望， E步。如果Z的值已知，就可以對模型引數做極大似然估計，M步。