泊松方程是靜電場問題的基礎，下面我們以此方法為基礎

自由空間中的泊松方程

可以證明這個方程的解為

用相同的方法，這個解記作格林函式 在自由空間下，任意泊松方程的

解可以寫為

這就是靜電場的疊加原理

如果不是自由空間，這個公式是不成立的，因為有除了空間內電荷，還有感應電荷分佈。

這個公式的完整形式是

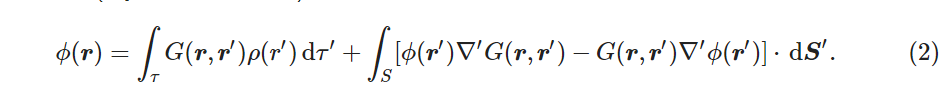
第一項就是之前算的源電荷的積分所產生的影響。第二項為邊界上的電勢和電荷的影響。

假設給定一個閉合區域，閉合區域內無電荷分佈，閉合區域接地，那麼不論區域外面的情況如何，區域內都沒有影響,見(2)

在有邊界情況下靜電場問題，通常有兩類邊界條件

1.給定邊界電勢，再求格林函式的時候要求再邊界處G(r,r')=0,那麼(2)只有前兩項的部分，由映象法，可以求出半無窮平面邊界和球外邊界的格林函式，由此可以解決靜電場問題

例子1：半無限大平面上方圓形環，帶電勢為V0，求上半平面電勢能。

由(2)等式，只需計算格林函式在邊界平面的法嚮導數，既可以解決這個問題。

例子2:  球面帶電導體，在上半球面的電壓為V，在下半球面的電壓為-V，求球外的電勢。

這個例子是利用球外的格林函式變為球座標表示，利用(2)的第二公式就能求解。

2.第二類邊界條件

給定邊界電勢的梯度（對應電荷密度），用(2)勢求解還需要知道在邊界上的平均電荷密度。要求格林函式滿足的條件於前面不同。所以求解起來比較困難，這裡就不講了

思考以及練習，求解球內邊界條件的格林函式，並利用球內邊界的格林函式解決第一類邊值問題。