CBOW

CBOW 是一個非常優秀的Word Embedding模型，其原理非常簡單，本文章嘗試深入模型內部，探索這個模型的效能和表現。

模型結構

準備

再介紹模型的網路結構之前，首先要介紹的是一個向量計算。假定特徵為，
$\bold{x}=(\bold{x_0},\bold{x_1},\cdots,\bold{x_{n-1}})$
其中$\bold{x_i}=(a_{i,0},a_{i,1},\cdots,a_{i,e-1})$

x = tf.placeholder(shape=[n, e], name='x', dtype=tf.float32)
y = tf.reduce_mean(x, axis = 1)
 

文字數字化

本節我們來討論文字數字話的技術。大家都知道，文字本身在計算機看來是有一個編號和一個渲染邏輯的。當我們提到一個文字的時候，計算機看來，這個文字就是一個編號，這個編號現在用的最多的就是UTF-8編碼；當我們看到一個文字的時候，計算機會找到文字編號對應的渲染邏輯，在LCD活著LED螢幕上點燃文字點陣。文字的點燃矩陣和文字的編碼都是沒有數學屬性的，例如“美麗”和“漂亮”在上述的表示中沒有任何數學上的關聯。

為了克服上述問題，一個廣泛使用的方法是one-hot，假定漢語中總共有$\sigma$個字，第$i$字用一個向量表示

這種表示忽略了詞彙本身的特徵，沒有挖掘出其合適的數學表示來。為了挖掘這種特性，通常的做法是先將文字表示成one-hot，然後作為一個神經網路層的輸入。這個神經網路的輸出為一個$e$維的向量，網路的行為可以用如下的數學公式表示
$\bold{y} = \bold{x}\bold{W}$
其中$\bold{x}$是詞的one-hot表示，$\bold{W}$是一個形狀為$\sigma \times e$的矩陣。W的每一行為$n$個從標準正態分佈中取樣的樣本。隨後$y$值會被當成神經網路的輸入。神經網路將通過梯度下降法學習W的最終表示，作為預料中詞彙的合適數字表示。

構建損失函式

目前有很多種構建損失函式的方法，最早的方法是使用RNN，RNN的損失函式是通過預測下個一個詞的分佈來完成的。CBOW構建損失函式的方法是通過左右預測中間的方法。

基於RNN的方法

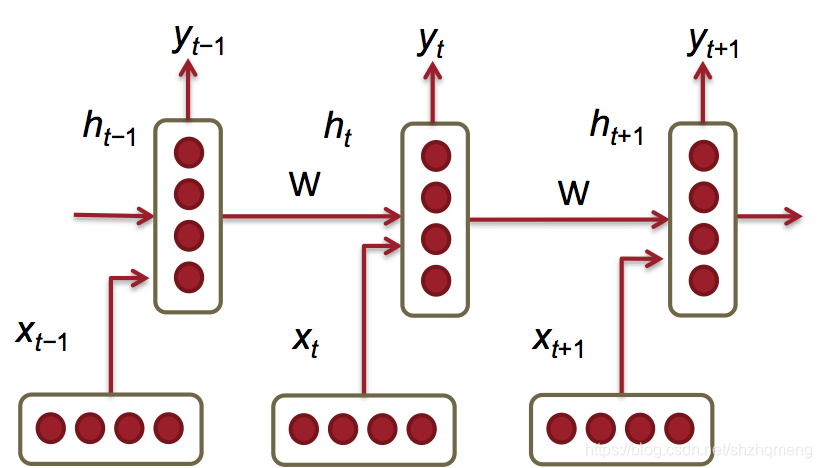
這種思路非常清晰，這裡就不贅述了。思路就是序列根據前面的序列預測下一個。

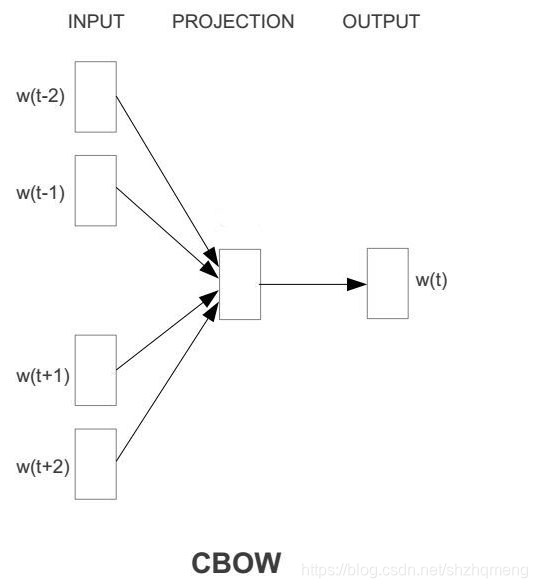
基於CBOW的方法

CBOW的思路是通過兩邊預測中間的詞。圖中的SUM函式就是我們在準備中介紹的向量化計算。$w(i)$就是文字數字化的輸出。

class WordEmbedding:
    def __init__(self, embeding_size, vocabulary_size, window_size):
        self.__graph = tf.Graph()
        self.__session = tf.Session(graph=self.__graph)

        self.__embeding_size = embeding_size
        self.__vocabulary_size = vocabulary_size
        self.__window_size = window_size
        self.__epoch_num = 10
        self.__embedding = None


    def embedingInit(self, vocabulary_size, embeding_size, x_onehot):
        embedding = tf.Variable(tf.random_uniform([vocabulary_size, embeding_size]))
        self.__embedding = embedding
        x_vec = tf.nn.embedding_lookup(embedding, x_onehot)
        return x_vec

    def graphCreate(self, x_vec):
        hidden_state = tf.reduce_mean(x_vec, axis=1)
        weight = tf.Variable(tf.truncated_normal(shape=[self.__embeding_size, self.__vocabulary_size]), dtype=tf.float32)
        bias = tf.Variable(tf.truncated_normal(shape=[1, self.__vocabulary_size]), dtype=tf.float32)
        y_logit = tf.matmul(hidden_state, weight) + bias
        y_softmax = tf.nn.softmax(y_logit)
        return y_logit, y_softmax

    def calculateLoss(self, logits, labels):
        cost_array = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=labels)
        return tf.reduce_sum(cost_array)

    def create_graph(self, batch_size):
        with self.__graph.as_default():
            self.__batch_size = tf.placeholder(dtype=tf.int32, name='batch_size')
            self.__x_ids = tf.placeholder(dtype=tf.int32, shape=[None, self.__window_size * 2], name="x_ids")
            self.__x_labels = tf.placeholder(dtype=tf.int32, shape=[None], name="x_lables")
            x_vec = self.embedingInit(self.__vocabulary_size, self.__embeding_size, self.__x_ids)
            tf.add_to_collection("infer", x_vec)
            y_logit, y_softmax = self.graphCreate(x_vec)
            cost = self.calculateLoss(y_logit, self.__x_labels)
            return cost, y_softmax


    def train(self, batch_sample, batch_label):
        batch_size = len(batch_sample[0])
        cost, y_softmax = self.create_graph(batch_size)
        with self.__graph.as_default():
            train = tf.train.AdamOptimizer().minimize(cost)
            self.__session.run(tf.global_variables_initializer())

            for i in range(self.__epoch_num):
                index_array = np.arange(len(batch_label))
                random.shuffle(index_array)
                for index in index_array:
                    if (len(batch_label[index]) != batch_size):
                        continue
                    _, lost_value = self.__session.run([train, cost], 
                                                       feed_dict={
                                                           self.__batch_size: batch_size,
                                                           self.__x_ids:batch_sample[index],
                                                           self.__x_labels:batch_label[index]
                                                       }
                                                    )
                    print(lost_value)

                save_path = tf.train.Saver(tf.trainable_variables(), max_to_keep=4).save(self.__session, "./data/model/model.ckpt")
                print(save_path)
	def infer(self, model_path):
		saver = tf.train.import_meta_graph(model_path + ".meta")
		with tf.Session() as sess:
			saver.restore(sess, model_path)
			y = tf.get_collection("infer")[0]
			graph = tf.get_default_graph()
			batch_size = graph.get_operation_by_name("batch_size").outputs[0]
			ids = graph.get_operation_by_name('x_ids').outputs[0]
			ret = sess.run(y, feed_dict={batch_size:[1], ids : [[2,3,4,5]]})