概述

這篇文章本來寫在了word文件裡，兩天倉促寫了這些東西，但不知不覺就搞了16頁的word，為了留存勞動成果，發一遍存到部落格上。文章幾乎一直在用失配後如何選擇新的合適的起點來說這個演算法，總之就是為了減少不必要的匹配，直接判掉某些匹配起始點，再就是匹配時主串是不會回退的。

說明

為了方便後文敘述，先定義幾個不正式的名詞。（這個純屬自己瞎造的詞，為了寫起來方便）

 

真字首，真字尾

對於一個長度為L的字串S，其真字首包括由它的前1個字元，或者前2個字元，前K個字元構成的字串，(1 <= K < L)。

例如對於S=”asdf”

它的真字首有”a”,”as”,”asd”三個，(“asdf”不算一個真子集,不符合條件)

類似地 其真字尾包括”f”,”df”,”sdf”

 

相等真前後綴

對於字串S，稱S的一個相等真前後綴為：

取S的一個子串sr,它既是S的真字首，也是S的真字尾

例如字串

S=”abaqwaba”,其相等真前後綴包括”aba”, ”a”

S=”abcweabc”,其相等真前後綴包括”abc”

S=”aaawaaa”,其相等真前後綴包括”aaa”, ”aa”, ”a”

S=”abababa”,其相等真前後綴包括”ababa”, “aba”, “a”

而對於S=”asdf”，它是沒有相等真前後綴的

 

針對的問題

 

設字串S1作為主串，字串S2作為待查詢串，詢問在串S1中能否找到一個連續的子串和S2相等，如果存在找出這個串的起始位置

 

例如 S1=”qaqabcde”, S2=”abc”  不需要程式，直接觀察也能發現”abc”在S1中出現了，起始位置是第4個字元開始。但是如果字串的長度足夠長，就需要藉助程式解決。

 

樸素匹配演算法

 

隨意構造一組資料，

樸素匹配演算法，也就是暴力嘗試

設字串S1的長度為L1，這裡L=14，設S2的長度為L2，這裡L2=5。

從字串S1中選取一個起點設為p1,從p1所在位置的字元開始，選取連續的L2長度個字元，由此形成的子串去和串S2逐位比較，如果每個位置都對應相同，則找到答案；否則，換一個起始點p1,再次作上述操作。為了找到答案，我們需要嘗試所有可能的起點p1。它的範圍包括,1<=p1<=L1-L2+1。在本例中，就是1到10這幾個位置上的字元可以作為起點。

這個思路很明確，程式碼也很快就能寫出。不過在本文中的程式碼在儲存字串時，選擇了從下標0開始儲存，例如儲存字串”abc”,它的第1，2，3個字元a,b,c對應的下標是0，1，2。所以在編寫程式時，這裡的p1從0開始(陣列下標原因)，表示從第一個字元開始作為起點，取連續的L2個字元和S2匹配。

這裡的p2最多取到9，因為下標最大到13，9到13是最後一組長度為5的連續子串

int judge(char *S1, char *S2)
{
	int ans = -1;
	int L1 = strlen(S1);//strlen函式求字串長度
	int L2 = strlen(S2);
	for (int i = 0;i <= L1 - L2;i++)//列舉起點p1，下標從0開始，所以下標最大到L1-L2，表示第L1-L2+1個字元
	{
		bool sign = true;
		for (int j = i;j<i + L2;j++)//從起點p1開始選取連續L2個字元，逐個比較
		{
			if (S1[j] != S2[j - i])
			{
				sign = false;
				break;
				//出現不同說明當前起點開始的子串不可行，break跳出去嘗試下一個起點
			}
		}
		if (sign)
		{
			ans = i;
			break;
		}
	}
	return ans;//返回值為-1時表示不存在
}

 

樸素演算法的問題

舉一個例子A

S1=”aaaabwaaaaaaaaaaabcac”

S2=”aaaabc”

按照上述演算法，第一輪比較是在第6個字元處失配

接著,程式嘗試第二個字元開始

模擬發現，前六個字元aaaabw其中任意一個作為起點都會失配.

從第7個字元作為起點匹配,在匹配了4個字元後出現失配

    

按上述演算法

下次從第8個字元開始嘗試，同樣，還是匹配了4個後才發現失配

嘗試第9，10，...，13個都是如此，其實這中間程式執行了很多沒有必要的比較

我們直接觀察很輕鬆就能發現，中間那一連串的a作起點都是不可行的，但是程式還是在每個位置開始連續作了4次比較。如果題目的測試資料足夠大，這樣的演算法會被輕鬆地卡掉。

 

上述演算法中，一旦出現失配。S1串就會重新選擇下一個起點，S2也是再次從其第一個字元開始去和新的S1中的子串比較。例如從第7個字元作起點時，匹配到了第11個字元出現失配，

然後又讓S2串回退到第8個字元為起點重新開始。然後8到12出現失配，回退，9到13..

如果我們能將一個串的匹配過程做到不回退，就可能提高效率

舉例B

匹配

S1起點選到第1個字元作為起點開始去和S2匹配，在第8個字元處失配，我們把失配位置(第8個字元)之前，也就是第2，3，4，5，6，7個字元開始作為起點的情況都列出來

S1的第2個字元作起點，第一次字元匹配就失配了

第3個字元作起點，匹配成功了一次

第4個字元作起點，第一次匹配就失配

第5個字元作起點，匹配成功

第6個字元作起點

第7個字元作起點

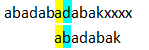
上面兩個例子都存在一些無意義的比較，每個例子主要說明了一種。或者說，有些比較是可以實現推斷出來不可行，直接避免的。

 

 

改進

可以用如下圖概括上述比較

假如在黃色部分是匹配成功了，在藍色p2位置處失配

下次如果選擇了一個起點為p1+k,也就是說下方圖中偏移量為k

即銀灰色部分長度為k

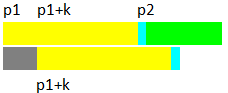
這次從p1+k位置起開始匹配

可以發現，這次匹配能否完全成功先不說，上次是S1串是從p1匹配到了藍色位置p2處才失配，如果現在所表示的下圖中,從p1+k開始的S1的紅色和S2的紫色部分沒有完全匹配，那這次以p1+k作為起點還不如之前用p1處作起點匹配的效果好，因為上次從p1匹配到了p2,而如果紅色和紫色部分出現不一致，從p1+k開始的匹配止於p2之前的某個位置，還不如從p1開始將匹配推進的遠。

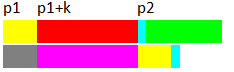
單獨把p1到p2-1這段拿出來

可以發現，假如把p1到p2-1這個串（上圖中原來的整個黃色部分）稱為串SP,串SP的紅色部分一定是SP的一個真字尾，串SP的紫色部分一定是它的一個真字首，如果這兩個前後綴不完全相等，就說明選擇之前選擇p1+k作起點匹配的效果一定是不如p1好的。

這說明有些起點的嘗試是應該直接避免掉的，判別方法就是，在假如上次起點選擇p1,失配位置為p2,這次選擇的起點為p1+k,如果從p1+k→p2-1這段字元和p1→p2-1-k 這段字元不完全匹配，這個起點就是絕對可以捨棄的。

所以對於樸素匹配演算法的一個改進點就是，在p1作起點匹配失敗後，不立即選擇p1+1作為起點再從頭匹配，而是先排除掉那些一定不會得到正解的起點。而剩餘下來的這些可選起點雖然不一定能得到完全匹配，但至少在上述的紅色和紫色部分匹配時是成功的，是有可能再向p2+1,p2+2...等更向右的地方繼續匹配，有可能取得完全匹配；而那些被排除的點是一定不會得到完全匹配。

例B體現的一種無意義的比較就是，假如失配位置是p2,在p2之前，有些起點是不必要嘗試的，例A的後文會提到。

例如在例B中p1=1,p2=8;在選擇p1+k=5和p1+k=7時，對應的串SP的真字首真字尾完全匹配。對應了起點選為5,7

而其他情況都不完全相等,這也分別對應了起點選為6，4，3，2

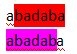
如果我們在某一個p2處失配之後，能快速知道在此之前的p1到p2-1這個字串中，使得滿足字首串p1→p2-1-k等於字尾串p1+k→p2-1的k，在下一次選擇起點時，直接從這些值中選下一個起點，就能避開所說的無意義的起點。而且，如果這樣的k可能有多個,比如本例中k=4或者6都行，而完全匹配即答案出現在哪個起點是不確定的，只是在本例中出現在了更小的k上，所以應該都做嘗試。如果有多個k符合，就先從這些k計算出的可行起點中選擇最小的來嘗試，在後文中，通過next[]陣列可以實現按這個順序嘗試。

待查詢的S2串的長度一定是大於等於p2-p1的，因為完全匹配的意思就是，如果從某個起點p1一直匹配到p2使得這個子串和S2一樣，則完成任務。在匹配過程中，每次匹配成功的長度p1→p2是不確定的，而每次失配之後都要快速計算對於當前p1->p2-1這個子串的所有應該避開的起點。就是說，對於長度為L2的串S2，我們要計算處它的所有子串1->2,1->3,1->4....,1->L2-1,1->L2這些長度的子串的k。

比如上述的S2 = abadabak

對於其子串

如果在匹配中遇到上述任意一種失配時，直接從這些滿足的條件裡選起點，就會減少計算量

例如

匹配到第7個時失配，之前匹配完全相同的部分是上述的情況6，只有字串ab滿足既是abadab的真字首也是真字尾，對應之前所說,這裡的p1=1,p2=7,k應取4所以下次起點直接選擇為p1+k=5

儘管這次選擇不一定就找到了最終解，但是已經避開了把起點選擇為2,3,4的必定失敗的情況。

 

所以現在要做的就是把上述8中情況裡對應的符合條件的子串都計算並記錄下來，匹配過程中失配後直接使用這些值。

 核心--next[]陣列

設一個字串S的長度為i，即其包含i個字元，next[i]=j表示的就是這個總長度i的字串的最長相等真前後綴。

例如 S=”aaaqwqaaa”的相等真前後綴有三個 a,aa,aaa，則記錄最大值 next[9]=3，表示這個S的第1到3個字元構成的字串，或者是倒數後三個字元構成的，就是最長相等真前後綴。

對於 abadaba 它的next陣列直接觀察也能得到

 next陣列下標 1 2 3 4 5 6 7

       對應的值  0 0 1 0 1 2 3

再比如     ababa

next陣列下標  1 2 3 4 5  

       對應的值  0 0 1 2 3

肉眼直接觀察也能得到，可是程式如何計算

設下圖黃色部分為串ST1,黃色加藍色部分為串ST2

我們假設下圖中黃色部分長度為len1,藍色位置為第len1+1個字元，且next[1],next[2],..,next[len1]的值都已計算出來過，現在要計算next[len1+1]的值，也就是計算串ST2的最長相等真前後綴。假設next[len1]=x1,這個值我們是知道的。x1就表示黃色部分字串的最長相等真前後綴

這個長度x1的部分用綠色標註出來

所以圖中綠色部分一樣，紫色位置為第x+1個字元,如果紫色位置和藍色位置的字元也相等，那麼next[len1+1]就是x+1,表示1到len1+1這個串的最長相等的真前後綴 就是如下圖長為x+1這部分

可是，如果藍色位置和紫色位置的字元不一樣呢，這時不能簡單把next[len1+1]賦值為0，

單獨看綠色這個部分，假如綠色部分長度為len2

設next[len2]=x2,這個值我們也是知道的，即綠色部分這個串的最長相等真前後綴長度為x2,我們用紅色標註出來x2

眼光再放回原來的長度為len1+1的串

綠色部分作為原來整個黃色串的真前後綴是相同的，紅色部分又是綠色串的最長相等真前後綴，圖中四個部分紅色的都應該是相同的

把開始部分的紅色之後第一個字元標註為深藍色

如果深藍色和後面藍色位置的字元也相同，而紅色部分又相同，則next[len1+1]=len2+1,即表示串ST2的最長相等真前後綴是如下圖這部分

如果深藍色位置和藍色位置還不相同，那麼，就繼續找紅色部分的最長真前後綴，即使用next[x2]，如果一直不匹配，就一直這樣重複，什麼時候停止呢，假如對紅色部分繼續上述操作，即先求next[x2];

如果next[x2]=0，說明紅色部分不存在相等的真前後綴，計算已經走到了邊界條件。這時直接比較串ST1（原來整個黃色部分）第一個字元和後面的藍色位置字元，相等則next[len1+1]=1,說明原來的長len1+1的串的最長相等真前後綴長度為1，否則說明ST2是不存在相等的真前後綴的，next[19]=0。

舉一個例子

黃色部分長18,觀察得出next[18]=8，即黃色部分的最長相等真前後綴為綠色標註的部分，長度8

所以下一步比較紫色位置和藍色位置

相等 則 next[19]=8+1=9（next[19] = next[18]+1）

如果不相等呢，例2

這個例子同樣next[18]=8

但紫色位置和藍色位置不同

所以繼續找綠色部分的next[8]=3,用紅色標註其對應的部分

所以下一步比較深藍色和藍色部分相同,next[19]=3+1=4（next[19] = next[ next[18] ] +1）

也有可能一直不同，例3

這時，已經把原來黃色部分的所有真前後綴嘗試完了，此時next[1]=0,就會直接去嘗試黃色部分的第一個字元和藍色位置字元，如果相等，next[19]=1;否則next[19]=0;這裡不相等，取後者

這時終止，next[19]=0;

所以，以上其實可以寫成一個遞推程式，因為,next[i]的計算依賴的是事先要知道

next[1],next[2],next[3],...,next[i-1]，我們可以從i=1向更大值遞推，而且，對於給定的字串S,不論它總長多少，next[1]=0是固定已知的，因為，單個字元不存在任何真字首，真字尾。

由此就可以去推next[2],然後next[3]可以由next[1],next[2]推出。這樣，對於串S，比如

S=”abcabc”,它的所有字首串a,ab,abc,abca,abcab,abcabc的各自的最長相等真前後綴都能求得

void get_next(char *p, int next[])
{
	int len = strlen(p);
	next[0] = -1;
	next[1] = 0;
	for (int i = 2;i <= len;i++)
	{
		int k = next[i - 1];
		while (k >= 0 && p[k - 1 + 1] != p[i - 1])//減一是對齊陣列下標，第i個字元在陣列中下標i-1
		{
			k = next[k];
		}
		next[i] = k + 1;
	}
}

next[i]不僅記錄了長度為i的串的最長的相等真前後綴。實際上也記錄了其所有的真前後綴

比如abababa  

其所有的相等真前後綴有a,aba,ababa,

next[7]=5只記錄了ababa，但對於ababa求next[5]即可得到aba,再對aba求next[3]=1得到a,所以藉助next[]陣列，我們能知道長度為L的字串的所有相等真前後綴，而且，長為L-1，L-2,,,1的串的所有真前後綴也都可由next[]陣列中找出。

得到next陣列後，就可以模擬匹配了，把待查詢串S2的next陣列求出來。

S1串起點p1先選擇第一個字元，然後和S2串匹配，假如匹配到p2位置失配，說明匹配成功的是串S2的前p2-p1個字元,然後我們求next[p2-p1];

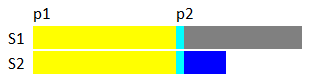
現在又回到了之前的問題，失配後選擇一個新的起點，之前我們說要避開所有無意義的起點，而有意義的，即有可能匹配成功的起點，是由p1到p2這個串的所有相等真前後綴得來，而這些前後綴都已經存在next[]中

對應上圖的例子

這個例子中p1=1,p2=8;

對於abadaba其相等真前後綴有 a, aba

所以先求next[8-1]=3;即綠色標註處都是相同的

這就相當於下一個起點選擇了第五個字元開始,相當於嘗試了abadaba的真前後綴aba

這樣還是失配了，next[3]=1;這相當於嘗試了abadaba的真前後綴a

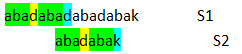
這時，已經把abadaba的所有真前後綴嘗試完了，也就是p2之前所有有意義的起點都試過了，next[1]=0;

下一次就會從第p2也就是8個字元開始作起點繼續匹配.

你可以發現，使用next陣列剛好可以將所有有意義的起點都嘗試一遍

再總結下S1和S2的匹配過程

S1總長L1,S2總長L2，假如現在已經走到了選擇p1處作為起點匹配，到p2處失配，失配之後就是要找黃色部分(設為串SP)的所有相等真前後綴，只有這些能產生有意義的起點。這些真前後綴就可以通過next陣列得到，設len1=p2-p1 表示黃色部分的長度，串S2的next[]陣列我們之前求過了，所以next[len]是知道的假如是x1，標註為紅色，則紅色部分相同，

所以下次起點可以選擇為p2-x1,

如果L2得到了完全匹配，程式就完成任務了，否則，要嘗試串SP的其他相等真前後綴，而這可由next[x1]得到，如next[x1]=x2;標註為深藍色，

再由此計算出新的起點p2-x2

如果匹配一直不成功，就不停使用next[]陣列轉移，最後當next[i]=0時說明SP（原來黃色部分）的所有真前後綴都嘗試完了，起點就不再從p1到p2之間選擇，下次起點直接從p2開始

寫成程式碼如下

judge函式求從S1串的p1處作起點去和長為L2的串匹配

int judge(char *S1, char *S2, int p1, int len)
{
	int i;
	for (i = 0;i<len;i++)
	{
		if (S1[p1 + i] != S2[i])
		{
			break;
		}
	}
	return i;//返回的i如果等於len說明匹配成功，否則說明完全匹配成功的有i個字元
}

match函式是改進後的匹配演算法，函式中的p1作為起點，在一次失配後不是把p1的值簡單加1，通過next[]陣列來找有意義的起點

int match(char *S1, char *S2)
{
	int len1 = strlen(S1);
	int len2 = strlen(S2);
	int p1 = 0;
	while (p1 <= len1 - len2)
	{
		int tp = judge(S1, S2, p1, len2);
		if (tp == len2)
		{
			break;//說明p1就是要找的起點
		}
		else
		{
			int k = Next[tp];
			p1 = p1 + tp - k;
		}
	}
	if (p1>len1 - len2)return -1;//表示匹配失敗
	else return p1;//否則返回起點
}

   

但還可以再改進，我們選擇了一個新的起點之後，從這個起點開始到p2是一定完全匹配的，而再程式裡judge函式重複計算了這些匹配。

例如

p1失配後選擇p2-x1作為起點，judge函式開始從這個起點對S2從頭開始匹配，但紅色部分是一定相同的，judge函式還是不夠高效。所以，KMP演算法不僅避免了選擇無效的起點，而且在選擇一個新的起點後，對S2的匹配也不需要從S2的第一個字元開始匹配，而是直接從S1中上次失配的位置開始，如上圖所示，從p2開始和S2中對應的位置(深藍色)開始匹配。避免掉的這部分對應了剛開始舉的例A

 再次改進

int judge(char *S1, char *S2, int p1, int len, int k)
{
	int i;
	for (i = max(k, 0);i<len;i++)  //直接跳過前K個字元的比較，因為前後綴相同重合
	{
		if (S1[p1 + i] != S2[i])
		{
			return i;
		}
	}
	return i;//返回的i如果等於len說明匹配成功，否則說明完全匹配成功的有i個字元
}

int kmp(char *S1, char *S2)
{
	int len1 = strlen(S1);
	int len2 = strlen(S2);
	int p1 = 0;
	int k = 0;
	while (p1 <= len1 - len2)
	{
		cout << p1 << "   sf" << endl;
		int tp = judge(S1, S2, p1, len2, k);
		if (tp == len2)
		{
			break;//說明p1就是要找的起點
		}
		else
		{
			k = Next[tp];
			p1 = p1 + tp - k;
		}
	}
	if (p1>len1 - len2)return -1;//表示匹配失敗
	else return p1;//否則返回起點
}

但是，程式碼可以更簡潔，judge函式優化掉

int kmp(char *S1, char *S2)
{
	int i = 0;
	int j = 0;
	int len1 = strlen(S1);
	int len2 = strlen(S2);
	while (i < len1 && j < len2)
	{
		if (j == -1 || S1[i] == S2[j])
		{
			i++;
			j++;
		}
		else
		{
			j = Next[j];
		}
	}
	if (j == len2)return i - j;
	else return -1;
}

 

模板題HDU1711

這個題目中是把匹配字串換成了匹配數列。

比如

1 2 1 2 3 1 2 3 1 3 2 1 2

1 2 3 1 3

第二個數列出現在第一個數列的第6到10這幾個位置。之前程式碼只要稍稍修改一下，把字元陣列改為整數陣列即可。

參考程式碼

#include <bits/stdc++.h>
using namespace std;
int N, M;
int Next[10010];
int shu1[1000010];
int shu2[10010];
void get_next(int next[])
{
	int len = M;
	next[0] = -1;
	next[1] = 0;
	for (int i = 2;i <= len;i++)
	{
		int k = next[i - 1];
		while (k >= 0 && shu2[k + 1 - 1] != shu2[i - 1])
		{
			k = next[k];
		}
		next[i] = k + 1;
	}
}
int judge(int p1, int len, int k)
{
	int i;
	for (i = max(k, 0);i<len;i++)
	{
		if (shu1[p1 + i] != shu2[i])
		{
			return i;
		}
	}
	return i;//返回的i如果等於len說明匹配成功，否則說明完全匹配成功的有i個字元
}
int kmp()
{
	int len1 = N;
	int len2 = M;
	int p1 = 0;
	int k = 0;
	while (p1 <= len1 - len2)
	{
		int tp = judge(p1, len2, k);
		if (tp == len2)
		{
			break;//說明p1就是要找的起點
		}
		else
		{
			k = Next[tp];
			p1 = p1 + tp - k;
		}
	}
	if (p1>len1 - len2)return -1;//表示匹配失敗
	else return p1 + 1;//否則返回起點
}

int main()
{
	int t;
	scanf("%d", &t);
	while (t--)
	{
		scanf("%d%d", &N, &M);
		for (int i = 0;i<N;i++)scanf("%d", &shu1[i]);
		for (int i = 0;i<M;i++)scanf("%d", &shu2[i]);
		get_next(Next);
		printf("%d\n", kmp());
	}
	return 0;
}

 

簡潔寫法

#include <bits/stdc++.h>
using namespace std;
#define MAXS 10005
int N, M, T;
int Next[MAXS];
int ar1[MAXS * 100];
int ar2[MAXS];

void getnext(int next[])
{
	int len = M;
	next[0] = -1;
	next[1] = 0;
	for (int i = 2;i <= len;i++)
	{
		int k = next[i - 1];
		while (k >= 0 && ar2[k + 1 - 1] != ar2[i - 1])
		{
			k = next[k];
		}
		next[i] = k + 1;
	}
}

int KMP()
{
	int len1 = N;
	int len2 = M;
	int j = 0;
	int i = 0;
	while (i < len1&&j < len2)
	{
		if (ar1[i] == ar2[j] || j == -1)
		{
			j++;
			i++;
		}
		else
		{
			j = Next[j];
		}
	}
	if (j == len2)return i - j + 1;
	else return -1;
}

int main()
{
	scanf("%d", &T);
	for (int i = 0;i < T;i++)
	{
		scanf("%d%d", &N, &M);
		for (int i = 0;i < N;i++)scanf("%d", &ar1[i]);
		for (int j = 0;j < M;j++) scanf("%d", &ar2[j]);
		getnext(Next);
		printf("%d\n", KMP());
	}
	return 0;
}