KMP演算法是迄今為止最為高效的字串匹配演算法。當然，在KMP演算法出現之前，有關字串的匹配問題當然經過了一個漫長的探索過程。從一開始最簡單的樸素字串匹配演算法，到Rabin-Karp演算法，再到有限自動機演算法等等，可以說任何一個偉大演算法的誕生都不可能是一朝一夕之功，在它之前一定有大量的理論及實驗的基礎。所以，想要徹底理解KMP演算法最好是從頭開始，對整個字串的匹配問題有個完整的瞭解。

但是，我在這篇博文中講的卻是對KMP演算法最簡單的理解。只能幫助大家瞭解KMP最基本的思路和應用。若要詳細瞭解，推薦《演算法導論》中的“字串匹配”一節。我沒有見過比這一章講解得更詳細的資料了。

所謂字串匹配，解決的問題就是在一段文字（text）之中尋找我們要匹配的模式（pattern）。文字和模式都是由字串構成的，模式的長度<=文字的長度。例如，模式為”aba”，文字為”abcbaba”，所謂字串匹配就是在文字中查詢模式出現的位置（一般以文字成功匹配的欄位的第一個字元的位置表示），這裡應該返回4。

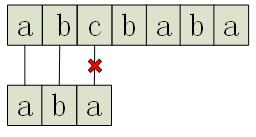
一種比較簡單的辦法是樸素字串匹配，就是一個字元一個字元去匹配。比如上面這個例子，一開始對文字和模式都是從頭開始匹配，效果如下圖：

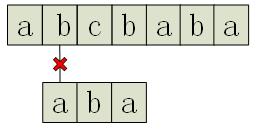
我們發現，第三個字元處文字為”c”，而模式為”a”，於是匹配失敗。那麼接下來，自然而然就能想到，把整個模式向右平移一位，再次進行匹配：

很遺憾，這次模式的第一個字元就沒能匹配成功。這樣，每次向後移動一位，依次匹配，若出現某一時刻模式的全部字元都能和它當時所對應的文字匹配，則匹配成功一次；繼續向後，直到模式的第一個字元對應的是文字的第(n - m + 1)個字元為止（其中，n為文字長度，m為字串長度），匹配結束。也就是說當模式的最後一個字元對應的是文字的最後一個字元時，就自然沒有必要再進行匹配了。

通過時間複雜度分析，可知樸素匹配演算法的時間複雜度為O((n−m+1)m)$O((n-m+1)m)$. 但是這個裡面有個問題，就是其實我們沒有必要在一次匹配失敗（成功）之後，向右移動一位繼續。而可以向右移動不止一位。

為什麼呢？還是看上面的例子，第一次匹配是，模式的第三個字元沒有和文字匹配，那同時也就說明了模式的前兩位和對應的文字是匹配的。我們可以確定模式未匹配的那一位所對應的文字的前一位（這裡就是文字的第二位）是b。而模式的第一位是a，那麼，顯然，a與b不同，往後移動一位讓a與b匹配就是多餘的，沒有必要的。

那麼應該往後移動幾位呢？可以想象，假如模式的第 i 位不能匹配，那麼，就需要移動模式，使得模式的前k位成為模式前 i - 1 位的字尾（k在此是個小於 i 的）。

先說明一下字串的字首，字尾：比如字串”abcde”中， “a”, “ab”, “abc”等等都是字首，而”cde”, “de”, “e” 等等都是字尾。也就是說，從字串頭開始截任意小於等於字串長度的字元，就是字首，而從後開始截任意長度就是字尾。

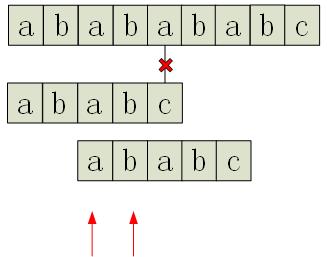
回到剛才的問題，為了能夠實現可能的匹配，需要模式向右偏移，使得模式以“最長的頭”匹配上剛才已經匹配的文字欄位的尾。也就是說尋找模式的前 i -1 項的字尾中能成為模式的最長字首的部分。而如果字尾中找不到字首，則將模式偏移 i 位即可。話有點抽象，看看這個例子：文字”ababababc”，模式”ababc”

同樣的，第一次匹配在模式的第5個字元處失敗，但是此時並沒有從後面一個字元開始重新匹配，而是向右移動兩位，為什麼是兩位呢，我們可以觀察一下紅箭頭指的兩位，因為模式的第5位匹配失敗，所以，現在我們看看能否在在模式前4位的字尾中找到模式的字首，剛好，字串”ab”可以作為模式前4位的字尾，同時也是模式的字首（字尾中最長的字首）。不難發現，只有這樣，才能使得這一次匹配是“可能有意義”的。

換句話說，可以通過對模式本身的計算，得出一個數組π$\pi$，其中π[index]$\pi [index]$告訴我們，如果模式的第index$index$位不能和文字匹配時，模式pattern$pattern$的前index−1$index-1$位中字尾中的最大字首的長度。比如，模式 "ababaca" 相對應的陣列π$\pi$為：

因為模式一般比文字短很多，所以，我們計算這個陣列消耗的計算量是可以接受的，尤其是模式比文字短很多的情況下。這樣，模式就應該向右偏移index−π[index]$index-\pi [index]$位。並且直接從模式的π[index]+1$\pi [index]+1$開始與文字上次沒有與模式成功匹配的位做比較。

總結一下上面的思路：

• 模式pattern$pattern$的第i$i$位pattern[i]$pattern[i]$與文字text$text$的第j$j$位text[j]$text[j]$不匹配了，就查詢π[j]$\pi [j]$；
• 重新開始比較pattern[π[j−1]]$pattern[\pi [j-1]]$與text[j]$text[j]$

上面的思路寫成程式碼如下：

def kmp(pattern, text):
    m, n = len(pattern), len(text)

    # i為模式的下標
    i = 0

    # 遍歷文字
    for j in range(n):
        # 要求i > 0的原因是如果模式的第一位都不能匹配，那就直接向右移動一格掃描文字
        while i > 0 and pattern[i] != text[j]:
            i = pi[i - 1]

        # 匹配成功，則繼續模式下一位與文字下一位的比對
        if pattern[i] == text[j]:
            i += 1

        # 整個模式匹配成功，輸出資訊
        if i == m:
            print("the pattern occurs at %d" % (j - i + 1))

            # 一次匹配完成，重新計算偏移量
            i = pi[i - 1]

程式碼中，我假設陣列 pi 已經被提前計算出來了。那現在的問題是怎麼計算陣列 pi ？

如果你已經理解了上面的程式碼，那麼計算 pi 就容易了，我們只需要稍微將上面的程式碼改一下，改成讓模式與模式自身匹配（當然是讓一個模式從第1位開始與另一個模式從第2位開始匹配），將每次匹配的最多字元的長度記錄下來就是所謂“字尾的最大字首”了。

因此，我的輔助函式 helper() 如下，負責計算偏移量陣列。

# 實際上是模式的字首與模式本身匹配
def helper(pattern):
    m = len(pattern)

    # pi的第1位是0，意思是如果pattern的第一個字元就不匹配的話，無偏移量
    pi = [0]
    k = 0

    # 遍歷模式，從第2位（也就是下標1開始）
    for j in range(1, m):

        # 不匹配，向右偏移，偏移量的計算還是依靠已經計算了部分的陣列pi
        # 這種思想有點類似於動態規劃，根據之前的計算結果計算新的結果
        # 每次計算的k值其實是當pattern[i]與文字不能匹配時的偏移量
        while k > 0 and pattern[k] != pattern[j]:
            k = pi[k - 1]
        # 匹配成功，k + 1得到最大字首
        if pattern[k] == pattern[j]:
            k += 1
        pi.append(k)
    return pi

把這兩段程式碼合成：
我省去了所有註釋，讓程式碼更清楚，就是下面的樣子，一共25行

def kmp(pattern, text):
    m, n = len(pattern), len(text)
    i = 0
    for j in range(n):
        while i > 0 and pattern[i] != text[j]:
            i = pi[i - 1]
        if pattern[i] == text[j]:
            i += 1
        if i == m:
            print("the pattern occurs at %d" % (j - i + 1))
            i = pi[i - 1]


def helper(pattern):
    m = len(pattern)

    pi = [0]
    k = 0

    for j in range(1, m):
        while k > 0 and pattern[k] != pattern[j]:
            k = pi[k - 1]
        if pattern[k] == pattern[j]:
            k += 1
        pi.append(k)
    return pi