我與機器學習 - [Today is LR] - [Logistic 迴歸]
今天學習的是Logistic Regresion 說他是迴歸,其實他主要處理分類問題,用迴歸來處理分類問題其思想是:根據現有的資料對分類邊界建立迴歸公式,以此進行分類。
優點:計算代價不高,易於理解和實現,
缺點:容易欠擬合,分類的精度可能不高
適用資料型別為:數值型和標稱型
sigmoid 函式 1 + e的-x次方分之一
為了實現Logistic迴歸分類器,我們可以在每個特徵上都乘以一個迴歸係數,然後把所有的結果都相加,將這個總和帶入到sigmoid函式,進而得到一個範圍在0~1之間的數,任何大於0.5的數被分入到1類,小於0.5 的數被分到0類。所以Logistic迴歸也被看作是一種概率估計。
sigmoid函式的輸入記為z,

如果採用向量的寫法,可以寫成 z = x ,他們表示將這兩個向量對應元素相乘然後全部相加後得到z,其中的x是輸入資料, 向量w是我們要尋找的最佳迴歸係數。為了尋找該最佳引數需要用到最優化理論中的一些知識。
梯度上升演算法:
梯度上升演算法基於的思想是,如果想要找到該函式的最大值,最好的方法就是沿著該函式的梯度方向進行探尋,如果梯度記為
則函式f(x,y)的梯度由下式表示,


根據公式已經可以預想到演算法怎麼完成了,初始化一個w,制定一個步長,比如0.1,演算法的思路就是,每次移動0.1然後重新計算該點處最佳的梯度,然後沿著梯度方向再次移動0.1,依次迴圈,直到誤差小於一定範圍,或者制定一個迴圈的次數,達到次數也可以停止。
隨機梯度演算法
剛剛的梯度上升演算法,在每次更新迴歸係數時需要遍歷整個資料集,當特徵很多時,計算的複雜度會很高。一種改進的方法是一次僅用一個樣本點來更新迴歸係數,該方法成為隨機梯度上升演算法。由於可以在新樣本到來時對分類器進行增量更新,所以隨機梯度上升演算法是一種線上學習演算法,與之對應的一次處理所有資料的方法叫做批處理。
處理資料中的缺失值:
使用該特徵其他的資料計算處的均值來填補該特徵下缺失的資料
使用特殊值如-1來填補缺失值
剔除有缺失資料的樣本
使用相似樣本的均值為缺失值填充
使用另外的機器學習演算法先預測缺失值
以上部分程式碼:https://github.com/HanGaaaaa/MLAProject/tree/master/Logistic
下面是數學理論支援部分和擴充套件部分:

如圖中所說的,這個式子後面要用到,化簡用的

對每個樣本來說:
所以對於m個樣本來說就是連續相乘。然後用對數似然求得對數似然函式後,求導。


接下來定義一個事件的機率:

對於logistic迴歸,其實是一種廣義的線性迴歸,因為他的機率的對數是一個線性迴歸,也叫做對數線性迴歸。
這樣的前提下,可以對sigmoid函式做一個證明。

所以這裡認為對於一個機率的對數是線性的模型,他的概率就是sigmoid函式。
以上求得的對數似然函式其實是求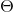
那麼對於logistic迴歸,有沒有損失函式呢。
可以把剛剛求得的對數似然取一個負號就是負對數似然,可以用此來當作他的損失函式。

詳細的推導為:

這個函式看起來很複雜,他的y的取值是0和1,當y取0時 loss = (1- y)* ln(1 + 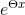
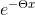
如果把y的取值變為-1和1,那麼函式會變得很漂亮。這裡需要一些處理。

處理之後y會可以放到e的指數上面。
最後引出softmax迴歸,他主要用來處理多分類問題:
依據就是當前這類在總類別中的佔比。

這部分實踐程式碼:https://github.com/HanGaaaaa/MLAPractice/tree/master/LogisticRegression