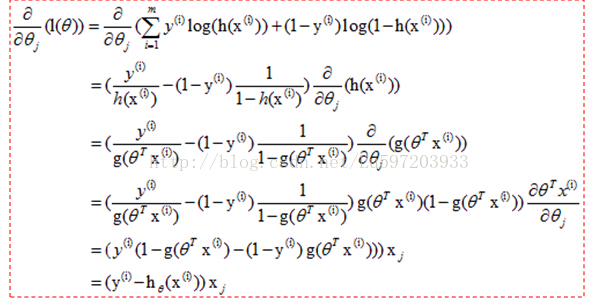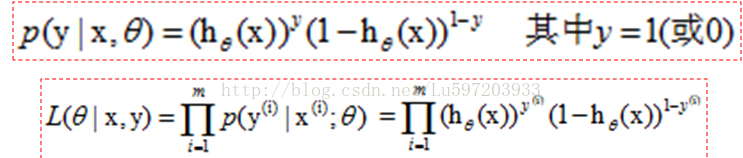機器學習實戰筆記5(logistic迴歸)
1:簡單概念描述
假設現在有一些資料點,我們用一條直線對這些點進行擬合(該線稱為最佳擬合直線),這個擬合過程就稱為迴歸。訓練分類器就是為了尋找最佳擬合引數,使用的是最優化演算法。
這就是簡單的線性迴歸問題,可以通過最小二乘法求解其引數,最小二乘法和最大似然估計見:http://blog.csdn.net/lu597203933/article/details/45032607。 但是當有一類情況如判斷郵件是否為垃圾郵件或者判斷患者癌細胞為惡性的還是良性的,這就屬於分類問題了,是線性迴歸所無法解決的。這裡以線性迴歸為基礎,講解logistic迴歸用於解決此類分類問題。
基於sigmoid函式分類:logistic迴歸想要的函式能夠接受所有的輸入然後預測出類別。這個函式就是sigmoid函式,它也像一個階躍函式。其公式如下:
其中: z = w0x0+w1x1+….+wnxn,w為引數, x為特徵
為了實現logistic迴歸分類器,我們可以在每個特徵上乘以一個迴歸係數,然後把所有的結果值相加,將這個總和結果代入sigmoid函式中,進而得到一個範圍在0~1之間的數值。任何大於0.5的資料被分入1類,小於0.5的資料被歸入0類。所以,logistic迴歸也可以被看成是一種概率估計。
亦即公式表示為:

g(z)曲線為:

此時就可以對標籤y進行分類了:
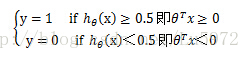
其中θTx=0 即θ0+θ1*x1+θ2*x2=0 稱為決策邊界即boundarydecision。
Cost function:
線性迴歸的cost function依據最小二乘法是最小化觀察值和估計值的差平方和。即:
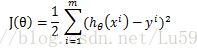
但是對於logistic迴歸,我們的cost fucntion不能最小化觀察值和估計值的差平法和,因為這樣我們會發現J(θ)為非凸函式,此時就存在很多區域性極值點,就無法用梯度迭代得到最終的引數(來源於AndrewNg video)。因此我們這裡重新定義一種cost function
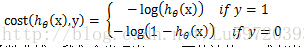
通過以上兩個函式的函式曲線,我們會發現當y=1,而估計值h=1或者當y=0,而估計值h=0,即預測準確了,此時的cost就為0,,但是當預測錯誤了cost就會無窮大,很明顯滿足cost function的定義。
可以將上面的分組函式寫在一起:
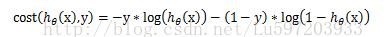
這樣得到總體的損失函式J(θ)為:
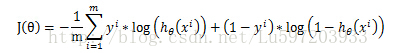
梯度上升法:基於的思想是要找到某函式的最大值,最好的方法是沿著該函式的梯度方向探尋。
該公式將一直被迭代執行,直到達到某個停止條件為止,比如迭代次數達到某個指定值或者演算法達到某個可以允許的誤差範圍。
這樣我們依據上面的J(θ)就可以得到梯度上升的公式:
當然上圖中少了個求和符號。這樣就得到
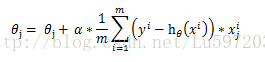
當然對於隨機化的梯度迭代每次只使用一個樣本進行引數更新,就為:
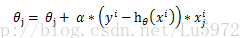
這也是下面程式碼中公式的來源。
例如:data=[1,2,3;4,5,6;7,8,9;10,11,12]為4個樣本點,3個特徵的資料集,,此時標籤為[1,0,0,0],
那麼用梯度上升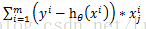
為什麼要採用上面的函式作為cost function?
Andrew Ng給的解釋是因為最小估計值和觀察值的差平方和為非凸函式,通過函式曲線觀察得到上面的cost function滿足條件。
這裡給出另外一種解釋——最大似然估計
我們知道hθ(x)≥0.5<後面簡用h>,此時y=1, 小於0.5,y=0. 那麼我們就用h作為y=1發生的概率,那麼當y=0時,h<0.5,此時不能用h作為y=0的概率,<因為最大似然的思想使已有的資料發生的概率最大化,小於0.5太小了>,我們可以用1-h作為y=0的概率,這樣就可以作為y=0的概率了,,然後只需要最大化聯合概率密度函式就可以了。
這樣聯合概率密度函式就可以寫成:
再轉換成對數似然函式,就和上面給出的似然函式一致了。
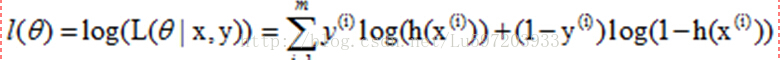
2:python程式碼的實現
(1) 使用梯度上升找到最佳引數
from numpy import *
#載入資料
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
#計算sigmoid函式
def sigmoid(inX):
return 1.0/(1+exp(-inX))
#梯度上升演算法-計算迴歸係數
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #轉換為numpy資料型別
labelMat = mat(classLabels).transpose()
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (labelMat - h)
weights = weights + alpha * dataMatrix.transpose() * error
return weights(2) 畫出決策邊界
#畫出決策邊界
def plotBestFit(wei):
import matplotlib.pyplot as plt
weights = wei.getA()
dataMat, labelMat = loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else: xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker='s')
ax.scatter(xcord2, ycord2, s = 30, c = 'green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]- weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1');
plt.ylabel('X2');
plt.show()(3) 隨機梯度上升演算法
梯度上升演算法在處理100個左右的資料集時尚可,但如果有數十億樣本和成千上萬的特徵,那麼該方法的計算複雜度就太高了。改進方法為隨機梯度上升演算法,該方法一次僅用一個樣本點來更新迴歸係數。它佔用更少的計算資源,是一種線上演算法,可以在資料到來時就完成引數的更新,而不需要重新讀取整個資料集來進行批處理運算。一次處理所有的資料被稱為批處理。
#隨機梯度上升演算法
def stocGradAscent0(dataMatrix, classLabels):
dataMatrix = array(dataMatrix)
m,n = shape(dataMatrix)
alpha = 0.1
weights = ones(n)
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights(4) 改進的隨機梯度上升演算法
#改進的隨機梯度上升演算法
def stocGradAscent1(dataMatrix, classLabels, numInter = 150):
dataMatrix = array(dataMatrix)
m,n = shape(dataMatrix)
weights = ones(n)
for j in range(numInter):
dataIndex = range(m)
for i in range(m):
alpha = 4 / (1.0+j+i) + 0.01 #alpha值每次迭代時都進行調整
randIndex = int(random.uniform(0, len(dataIndex))) #隨機選取更新
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del[dataIndex[randIndex]]
return weights注意:主要做了三個方面的改進:<1>alpha在每次迭代的時候都會調整,這會緩解資料波動或者高頻波動。<2>通過隨機選取樣本來更新迴歸係數,這樣可以減少週期性波動<3>增加了一個迭代引數
3:案例—從疝氣病症預測病馬的死亡率
(1) 處理資料中缺失值方法:
但是對於類別標籤丟失的資料,我們只能採用將該資料丟棄。
(2) 案例程式碼
#案例-從疝氣病症預測病馬的死亡率
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
def colicTest():
frTrain = open('horseColicTraining.txt')
frTest = open('horseColicTest.txt')
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent1(trainingSet, trainingLabels, 500)
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr = []
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec)
print 'the error rate of this test is: %f' % errorRate
return errorRate
def multiTest():
numTests = 10;errorSum = 0.0
for k in range(numTests):
errorSum += colicTest()
print 'after %d iterations the average error rate is: %f' %(numTests, errorSum/float(numTests))
4:總結
Logistic迴歸的目的是尋找一個非線性函式sigmoid的最佳擬合引數,求解過程可以由最優化演算法來完成。在最優化演算法中,最常用的就是梯度上升演算法,而梯度上升演算法又可以簡化為隨機梯度上升演算法。
隨機梯度上升演算法和梯度上升演算法的效果相當,但佔用更少的計算資源。此外,隨機梯度是一種線上演算法,可以在資料到來時就完成引數的更新,而不需要重新讀取整個資料集來進行批處理運算。
註明:1:本筆記來源於書籍<機器學習實戰>
2:logRegres.py檔案及筆記所用資料在這下載(http://download.csdn.net/detail/lu597203933/7735821).
歡迎轉載或分享,但請務必宣告文章出處。 (新浪微博:小村長zack, 歡迎交流!)