納什均衡（Nash equilibrium），又稱為非合作博弈均衡，是博弈論的一個重要策略組合，以約翰·納什命名。

納什均衡是指博弈中這樣的局面，對於每個參與者來說，只要其他人不改變策略，他就無法改善自己的狀況。納什證明了在每個參與者都只有有限種策略選擇並允許混合策略的前提下，納什均衡定存在。

以兩家公司的價格大戰為例，價格大戰存在著兩敗俱傷的可能，在對方不改變價格的條件下既不能提價，否則會進一步喪失市場;也不能降價,因為會出現賠本甩賣。於是兩家公司可以改變原先的利益格局，通過談判尋求新的利益評估分攤方案。相互作用的經濟主體假定其他主體所選擇的戰略為既定時，選擇自己的最優戰略的狀態，也就是納什均衡。

含義

假設有n個局中人蔘與博弈，如果某情況下無一參與者可以獨自行動而增加收益（即為了自身利益的最大化，沒有任何單獨的一方願意改變其策略的），則此策略組合被稱為納什均衡。所有局中人策略構成一個策略組合（Strategy Profile）。納什均衡，從實質上說，是一種非合作博弈狀態。

納什均衡達成時，並不意味著博弈雙方都處於不動的狀態，在順序博弈中這個均衡是在博弈者連續的動作與反應中達成的。納什均衡也不意味著博弈雙方達到了一個整體的最優狀態，需要注意的是，最優策略不一定達成納什均衡，嚴格劣勢策略不可能成為最佳對策，而弱優勢和弱劣勢策略是有可能達成納什均衡的。在一個博弈中可能有一個以上的納什均衡，而囚徒困境中有且只有一個納什均衡。

分類

納什均衡可以分成兩類：“純戰略納什均衡”和“混合戰略納什均衡”。

要說明純戰略納什均衡和混合戰略納什均衡，要先說明純戰略和混合戰略。

所謂純戰略是提供給玩家要如何進行賽局的一個完整的定義。特別地是，純戰略決定在任何一種情況下要做的移動。戰略集合是由玩家能夠施行的純戰略所組成的集合。而混合戰略是對每個純戰略分配一個機率而形成的戰略。混合戰略允許玩家隨機選擇一個純戰略。混合戰略博弈均衡中要用概率計算，因為每一種策略都是隨機的，達到某一概率時，可以實現支付最優。因為機率是連續的，所以即使戰略集合是有限的，也會有無限多個混合戰略。

當然，嚴格來說，每個純戰略都是一個“退化”的混合戰略，某一特定純戰略的機率為 1

故“純戰略納什均衡”，即參與之中的所有玩家都玩純戰略；而相應的“混合戰略納什均衡”，之中至少有一位玩家玩混合戰略。並不是每個賽局都會有純戰略納什均衡，例如“錢幣問題"就只有混合戰略納什均衡，而沒有純戰略納什均衡。不過，還是有許多賽局有純戰略納什均衡（如協調賽局，囚徒困境和獵鹿賽局）。甚至，有些賽局能同時有純戰略和混合戰略均衡。

經典案例-囚徒困境

假設有兩個小偷A和B聯合犯事、私入民宅被警察抓住。警方將兩人分別置於不同的兩個房間內進行審訊，對每一個犯罪嫌疑人，警方給出的政策是：如果一個犯罪嫌疑人坦白了罪行，交出了贓物，於是證據確鑿，兩人都被判有罪。如果另一個犯罪嫌疑人也作了坦白，則兩人各被判刑8年；如果另一個犯罪嫌人沒有坦白而是抵賴，則以妨礙公務罪（因已有證據表明其有罪）再加刑2年，而坦白者有功被減刑8年，立即釋放。如果兩人都抵賴，則警方因證據不足不能判兩人的偷竊罪，但可以私入民宅的罪名將兩人各判入獄1年。

關於案例，顯然最好的策略是雙方都抵賴，結果是大家都只被判1年。但是由於兩人處於隔離的情況，首先應該是從心理學的角度來看，當事雙方都會懷疑對方會出賣自己以求自保、其次才是亞當·斯密的理論，假設每個人都是“理性的經濟人”，都會從利己的目的出發進行選擇。這兩個人都會有這樣一個盤算過程：假如他坦白，如果我抵賴，得坐10年監獄，如果我坦白最多才8年；假如他要是抵賴，如果我也抵賴，我就會被判一年，如果我坦白就可以被釋放，而他會坐10年牢。綜合以上幾種情況考慮，不管他坦白與否，對我而言都是坦白了划算。兩個人都會動這樣的腦筋，最終，兩個人都選擇了坦白，結果都被判8年刑期。

基於經濟學中“理性的經濟人”的前提假設，兩個囚犯符合自己利益的選擇是坦白招供，原本對雙方都有利的策略不招供從而均被判處一年就不會出現。這樣兩人都選擇坦白的策略以及因此被判8年的結局，納什均衡”首先對亞當·斯密的“看不見的手”的原理提出挑戰：按照斯密的理論，在市場經濟中，每一個人都從利己的目的出發，而最終全社會達到利他的效果。但是我們可以從“納什均衡”中引出“看不見的手”原理的一個悖論：從利己目的出發，結果損人不利己，既不利己也不利他。

經典案例-硬幣正反

你正在圖書館枯坐，一位陌生美女主動過來和你搭訕，並要求和你一起玩個數學遊戲。美女提議：“讓我們各自亮出硬幣的一面，或正或反。如果我們都是正面，那麼我給你3元，如果我們都是反面，我給你1元，剩下的情況你給我2元就可以了。”那麼該不該和這位姑娘玩這個遊戲呢？這基本是廢話，當然該。問題是，這個遊戲公平嗎？

每一種遊戲依具其規則的不同會存在兩種納什均衡，一種是純策略納什均衡，也就是說玩家都能夠採取固定的策略(比如一直出正面或者一直出反面)，使得每人都賺得最多或虧得最少；或者是混合策略納什均衡，而在這個遊戲中，便應該採用混合策略納什均衡。

 假設我們出正面的概率是x，反面的概率是1-x，美女出正面的概率是y，反面的概率是1-y。為了使利益最大化，應該在對手出正面或反面的時候我們的收益都相等（不然在這個遊戲中，對方可以改變正反面出現的概率讓我們的期望收入減少），由此列出方程就是：

3y + (-2)*(1-y)=(-2) * y + 1*( 1-y )

解方程得y=3/8。

同樣，美女的收益，列方程

-3x + 2( 1-x)= 2x+ (-1) * ( 1-x)

解得x也等於3/8。

而美女每次的期望收益則是 2(1-x)- 3x = 1/8元。這告訴我們，在雙方都採取最優策略的情況下，平均每次美女贏1/8元。其實只要美女採取了(3/8,5/8)這個方案，不論你再採用什麼方案，都是不能改變局面的。

經典案例-餓獅博弈

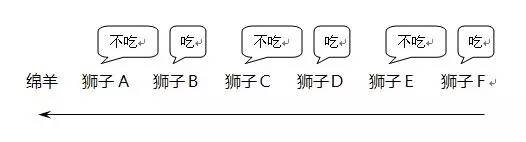
假設有A、B、C、D、E、F六隻獅子（強弱從左到右依次排序）和一隻綿羊。假設獅子A吃掉綿羊後就會打盹午睡，這時比A稍弱的獅子B就會趁機吃掉獅子A，接著B也會午睡，然後獅子C就會吃掉獅子B，以此類推。那麼問題來了，獅子A敢不敢吃綿羊？

為簡化說明，我們先給出此題的解法。該題須採用逆向分析法，也就是從最弱的獅子F開始分析，依次前推。假設獅子E睡著了，獅子F敢不敢吃掉獅子E？答案是肯定的，因為在獅子F的後面已沒有其它獅子，所以獅子F可以放心地吃掉午睡中的獅子E。

繼續前推，既然獅子E睡著會被獅子F吃掉，那麼獅子E必然不敢吃在他前面睡著的獅子D。

再往前推，既然獅子E不敢吃掉獅子D，那麼D則可以放心去吃午睡中的獅子C。依次前推，得出C不吃，B吃，A不吃。所以答案是獅子A不敢吃掉綿羊。

推理結果如下圖： 

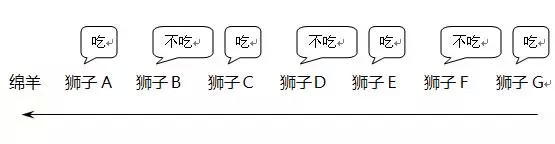
但是，如果我們在獅子F的後面增加了一隻獅子G，總數變成7只，用逆向分析法按照上題步驟再推一次，很容易得出結論：獅子G吃，獅子F不吃，E吃，D不吃，C吃，B不吃，A吃。這次的答案變成了獅子A敢吃掉綿羊。

對比兩次博弈我們發現，獅子A敢不敢吃綿羊取決於獅子總數的奇偶性，總數為奇數時，A敢吃掉綿羊；總數為偶數時，A則不敢吃。因此，總數為奇數和總數為偶數的獅群博弈結果形成了兩個穩定的納什均衡點。

經典案例-智豬博弈

豬圈裡有兩頭豬，一頭大豬，一頭小豬。豬圈的一邊有個踏板，每踩一下踏板，在遠離踏板的豬圈的另一邊的投食口就會落下少量的食物。如果有一隻豬去踩踏板，另一隻豬就有機會搶先吃到另一邊落下的食物。當小豬踩動踏板時，大豬會在小豬跑到食槽之前剛好吃光所有的食物；若是大豬踩動了踏板，則還有機會在小豬吃完落下的食物之前跑到食槽，爭吃到另一半殘羹。

那麼，兩隻豬各會採取什麼策略？答案是：小豬將選擇“搭便車”策略，也就是舒舒服服地等在食槽邊；而大豬則為一點殘羹不知疲倦地奔忙於踏板和食槽之間。

原因何在？因為，小豬踩踏板將一無所獲，不踩踏板反而能吃上食物。對小豬而言，無論大豬是否踩動踏板，不踩踏板總是好的選擇。反觀大豬，已明知小豬是不會去踩動踏板的，自己親自去踩踏板總比不踩強吧，所以只好親力親為了。

智豬博弈帶來的思考

“智豬博弈”告訴我們：在一個雙方公平、公正、合理和共享競爭環境中，有時佔優勢的一方最終得到的結果卻有悖於他的初始理性。

比如，在某種新產品剛上市，其效能和功用還不為人所熟識的情況下，如果進行新產品生產的不僅是一家小企業，還有其他生產能力和銷售能力更強的企業。那麼，小企業完全沒有必要作出頭鳥，自己去投入大量廣告做產品宣傳，只要採用跟隨戰略即可。

“智豬博弈”告訴我們，誰先去踩這個踏板，就會造福全體，但多勞卻並不一定多得。

在現實生活中，很多人都只想付出最小的代價，得到最大的回報，爭著做那隻坐享其成的小豬。“一個和尚挑水喝，兩個和尚擡水喝，三個和尚沒水喝”說的正是這樣一個道理。這三個和尚都想做“小豬”，卻不想付出勞動，不願承擔起“大豬”的義務，最後導致每個人都無法獲得利益。

證券市場中的“智豬博弈”

金融證券市場是一個群體博弈的場所，其真實情況非常複雜。在證券交易中，其結果不僅依賴於單個參與者自身的策略和市場條件，也依賴其他人的選擇及策略。

在“智豬博弈”的情景中，大豬是佔據比較優勢的，但是，由於小豬別無選擇，使得大豬為了自己能吃到食物，不得不辛勤忙碌，反而讓小豬搭了便車，而且比大豬還得意。這個博弈中的關鍵要素是豬圈的設計， 即踩踏板的成本。

證券投資中也是有這種情形的。例如，當莊家在底位買入大量股票後，已經付出了相當多的資金和時間成本，如果不等價格上升就撤退，就只有接受虧損。

所以，基於和大豬一 樣的貪吃本能，只要大勢不是太糟糕，莊家一般都會擡高股價，以求實現手中股票的增值。這時的中小散戶，就可以對該股追加資金，當一隻聰明的“小豬”，而讓 “大豬”莊家力擡股價。當然，這種股票的發覺並不容易，所以當“小豬”所需要的條件，就是發現有這種情況存在的豬圈，並衝進去。這樣，你就成為一隻聰明的 “小豬”。

從散戶與莊家的策略選擇上看，這種博弈結果是有參考價值的。例如，對股票的操作是需要成本的，事先、事中和事後的資訊處理，都需要金錢與時間成本的投入，如行業分析、企業調研、財務分析等。

一旦已經付出，機構投資者是不太甘心就此放棄的。而中小散戶，不太可能事先支付這些高額成本，更沒有資金控盤操作，因此只能採取小豬的等待策略。等到莊家動手為自己覓食而主動出擊時，散戶就可以坐享其成了。

股市中，散戶投資者與小豬的命運有相似之處，沒有能力承擔炒作成本，所以就應該充分利用資金靈活、成本低和不怕被套的優勢，發現並選擇那些機構投資者已經或可能坐莊的股票，等著大豬們為自己服務。

由此看到，散戶和機構的博弈中，散戶並不是總沒有優勢的，關鍵是找到有大豬的那個食槽，並等到對自己有利的遊戲規則形成時再進入。

遺憾的是，在股市中，很多作為“小豬”的散戶不知道要採取等待策略。更不知道讓“大豬”們去表現，在“大豬”們拉動股票價格後從中獲取利潤，才是“小豬”們的最佳選擇。

作為“小豬”，還要學會特立獨行。行動前，不用也不需要從其他“小豬”那裡得到肯定；行動時，認同且跟隨你的“小豬”越多，則你出錯的可能也就越大。簡單地說，就是不要從眾，而是跟隨“大豬”。

當然股市中的金融機構要比模型中的大豬聰明的多，並且不守遊戲規則，他們不會甘心為小豬們踩踏板。事實上，他們往往會選擇破壞這個博弈的規矩，甚至重新建立新規則。

比如他們可以把踏板放在食槽旁邊，或者可以遙控，這樣小豬們就失去了搭便車的機會。例如，金融機構和上市公司串通，散佈虛假的利空訊息，這就類似於踩踏板前騙小豬離開食槽，好讓自己飽餐一頓。

當然金融市場中的很多“大豬”也並不聰明，他們的表現欲過強，太喜歡主動地創造市場反應，而不只是對市場作出反應。短期來看，他們可以很容易地左右市場，操縱價格，做膽大妄為的造市者。

這些“大豬”們並不知道自己要小心謹慎、如履薄冰，他們不知道自己的力量不如想象的那樣強大到可以無敵於天下。自然而然地，每一年都會有一些高估自己的“大豬”倒下，倖存的“大豬”在經過優勝劣汰之後會變得更加強壯。

不過，無論是多麼強壯的“大豬”，只要過於自信、高估自己控制市場的能力，總會倒下。

俗話說“家家有本難唸的經”，在股市中，“大豬”有“大豬”的難處，“小豬”有“小豬”的難處。儘管“大豬”“小豬”只要瞭解自身處境，採取相應的策略就會成功，然而理性是有限的，確定的成功總是很難獲得。

參考網址：