題目連結：https://codeforces.com/contest/1081/problem/C

題意：給n，m，k，用m中顏色給1*n的方塊塗色，滿足有k個小方塊與其左邊是不同的（除開第一個），求出塗色方案數。

題解：參考官方題解。

解法一：

我們可以在n-1塊方塊選擇k個方塊，來塗色，滿足其與左邊不同，即是,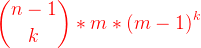

我們來解釋下，先選出k個，然後首先第一個可以取m種顏色，相對應的其它k個每個方塊都能取m-1種顏色。

假設我們選好了第一塊的顏色，那麼要是下一個不是選出k個的其中一個，其顏色一定與第一塊相同，要是在選出k箇中的其中一個，那麼我們要滿足這兩個不同，只能有m-1中顏色可以選擇。以此類推。

程式碼：

#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long LL;

const int maxn=2010;
const LL mod=998244353;

LL jie[maxn],ni[maxn];

LL fast_pow(LL a,LL n)
{
    LL sum=1;
    while(n)
    {
        if(n&1) sum=sum*a%mod;
        a=a*a%mod;
        n/=2;
    }
    return sum;
}

void init()
{
    jie[0]=jie[1]=1;

    for(int i=2;i<maxn;i++)
        jie[i]=1LL*jie[i-1]*i%mod;

    ni[2000]=fast_pow(jie[2000],mod-2);

    for(int i=2000;i>=1;i--) ///費馬小定理線性篩階乘逆元
    {
        ni[i-1]=1LL*ni[i]*i%mod;
    }
}

int main()
{
    LL n,m,k;
    init();

    while(~scanf("%lld%lld%lld",&n,&m,&k))
    {
        printf("%lld\n",jie[n-1]*ni[k]%mod*ni[n-1-k]%mod*m%mod*fast_pow(m-1,k)%mod);
    }
    return 0;

}
 

解法二：

我們設dp[n][m] 表示在1到n個方塊中，有m個小方塊與其左邊的顏色不同，那麼我們考慮第i個小方塊顏色與第i-1塊小方塊顏色是否相同

即：dp[i][j]=dp[i-1][j]+dp[i-1][j-1]*(m-1)。

程式碼：

#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long LL;

const int maxn=2010;
const LL mod=998244353;

LL dp[maxn][maxn];

int main()
{
        int n,m,k;

        while(~scanf("%d%d%d",&n,&m,&k))
        {
            dp[1][0]=m;

            for(int i=1;i<n;i++)
            {
                for(int j=0;j<=k;j++)///轉移方程不一定非要按照說的去，也可以變下，本質上也是相同的
                {
                    dp[i+1][j]=dp[i+1][j]+dp[i][j]%mod;
                    dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j]*(m-1)%mod)%mod;
                }

            }
            printf("%lld\n",dp[n][k]%mod);
        }
        return 0;
}