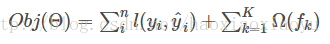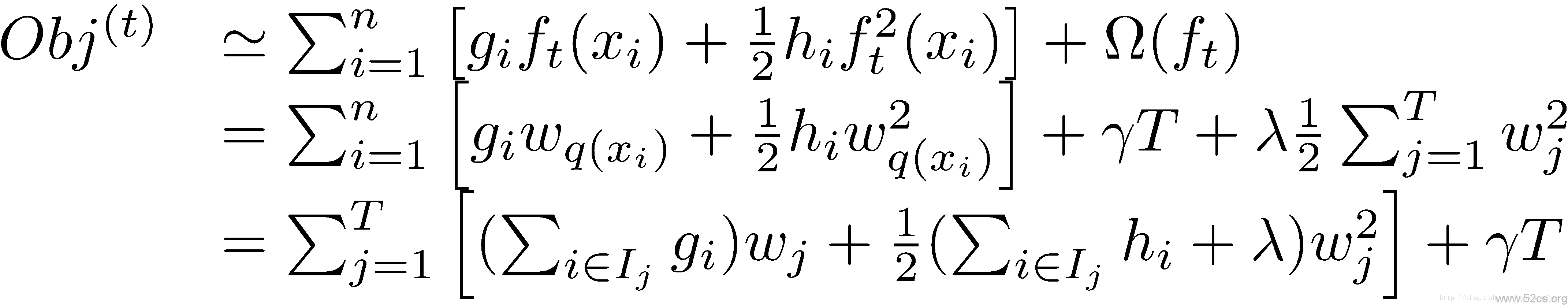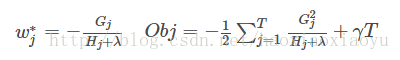轉自：XGBoost與Boosted Tree | 我愛計算機 1. 前言    應 @龍星鏢局 兄邀請寫這篇文章。作為一個非常有效的機器學習方法，Boosted Tree是資料探勘和機器學習中最常用的演算法之一。因為它效果好，對於輸入要求不敏感，往往是從統計學家到資料科學家必備的工具之一，它同時也是kaggle比賽冠軍選手最常用的工具。最後，因為它的效果好，計算複雜度不高，也在工業界中有大量的應用。

2. Boosted Tree的若干同義詞    說到這裡可能有人會問，為什麼我沒有聽過這個名字。這是因為Boosted Tree有各種馬甲，比如GBDT, GBRT (gradient boosted regression tree)，MART[1]，LambdaMART也是一種boosted tree的變種。網上有很多介紹Boosted tree的資料，不過大部分都是基於Friedman的最早一篇文章Greedy Function Approximation: A Gradient Boosting Machine的翻譯。個人覺得這不是最好最一般地介紹boosted tree的方式。而網上除了這個角度之外的介紹並不多。這篇文章是我個人對於boosted tree和gradient boosting 類演算法的總結，其中很多材料來自於我TA UW機器學習時的一份講義[2]。

3. 有監督學習演算法的邏輯組成    要講boosted tree，要先從有監督學習講起。在有監督學習裡面有幾個邏輯上的重要組成部件[3]，初略地分可以分為：模型，引數 和 目標函式。

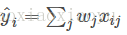
i. 模型和引數    模型指給定輸入  如何去預測 輸出 。比較常見的模型如線性模型（包括線性迴歸和logistic regression）採用了線性疊加的方式進行預測 。其實這裡的預測y可以有不同的解釋，比如可以用它來作為迴歸目標的輸出，或者進行sigmoid 變換得到概率，或者作為排序的指標等。而一個線性模型根據  的解釋不同（以及設計對應的目標函式）用到迴歸，分類或排序等場景。引數指需要學習的東西，線上性模型中，引數是指線性係數 

ii. 目標函式：損失 + 正則    模型和引數本身指定了給定輸入我們如何做預測，但是沒有告訴我們如何去尋找一個比較好的引數，這個時候就需要目標函式登場了。一般的目標函式包含下面兩項    常見的誤差函式有 比如平方誤差  ，logistic誤差函式（ ）等。而對於線性模型常見的正則化項有L2正則和L1正則。這樣目標函式的設計來自於統計學習裡面的一個重要概念叫做Bias-variance tradeoff[4]。比較感性的理解，Bias可以理解為假設我們有無限多資料的時候，可以訓練出最好的模型所拿到的誤差。而Variance是因為我們只有有限資料，其中隨機性帶來的誤差。目標中誤差函式鼓勵我們的模型儘量去擬合訓練資料，這樣相對來說最後的模型會有比較少的 bias。而正則化項則鼓勵更加簡單的模型。因為當模型簡單之後，有限資料擬合出來結果的隨機性比較小，不容易過擬合，使得最後模型的預測更加穩定。

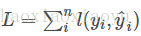
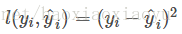
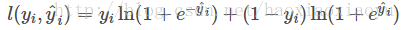
iii. 優化演算法    講了這麼多有監督學習的基本概念，為什麼要講這些呢？ 是因為這幾部分包含了機器學習的主要成分，也是機器學習工具設計中劃分模組比較有效的辦法。其實這幾部分之外，還有一個優化演算法，就是給定目標函式之後怎麼學的問題。之所以我沒有講優化演算法，是因為這是大家往往比較熟悉的“機器學習的部分”。而有時候我們往往只知道“優化演算法”，而沒有仔細考慮目標函式的設計的問題，比較常見的例子如決策樹的學習，大家知道的演算法是每一步去優化gini entropy，然後剪枝，但是沒有考慮到後面的目標是什麼。

4. Boosted Tree i. 基學習器：分類和迴歸樹（CART）    話題回到boosted tree，我們也是從這幾個方面開始講，首先講模型。Boosted tree 最基本的組成部分叫做迴歸樹(regression tree)，也叫做CART[5]。 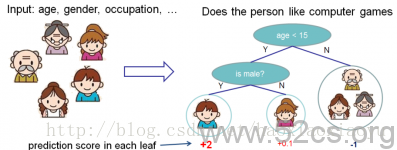    上面就是一個CART的例子。CART會把輸入根據輸入的屬性分配到各個葉子節點，而每個葉子節點上面都會對應一個實數分數。上面的例子是一個預測一個人是否會喜歡電腦遊戲的 CART，你可以把葉子的分數理解為有多可能這個人喜歡電腦遊戲。有人可能會問它和decision tree的關係，其實我們可以簡單地把它理解為decision tree的一個擴充套件。從簡單的類標到分數之後，我們可以做很多事情，如概率預測，排序。(此處，原本是喜歡、不喜歡的分類問題，假設由1，0來分別表示，則可以理解分數的形成了，但是涉及到副分，可能是將喜歡和不喜歡進一步細分，並用分數來表示：不喜歡：-2，-1，喜歡：1，2)

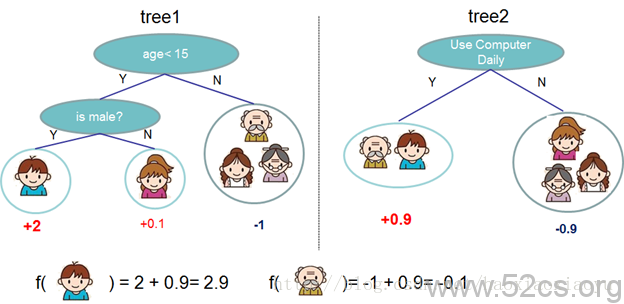
ii. Tree Ensemble    一個CART往往過於簡單無法有效地預測，因此一個更加強力的模型叫做tree ensemble。 

  在上面的例子中，我們用兩棵樹來進行預測。我們對於每個樣本的預測結果就是每棵樹預測分數的和。到這裡，我們的模型就介紹完畢了。現在問題來了：第一個問題，我們常見的隨機森林和boosted tree和tree ensemble有什麼關係呢？如果你仔細的思考，你會發現RF和boosted tree的模型都是tree ensemble，只是構造（學習）模型引數的方法不同。第二個問題：在這個模型中的“引數”是什麼。在tree ensemble中，引數對應了樹的結構，以及每個葉子節點上面的預測分數。

  最後一個問題當然是如何學習這些引數。在這一部分，答案可能千奇百怪，但是最標準的答案始終是一個：定義合理的目標函式，然後去嘗試優化這個目標函式。在這裡我要多說一句，因為決策樹學習往往充滿了heuristic。 如先優化吉尼係數，然後再剪枝，限制最大深度，等等。其實這些heuristic的背後往往隱含了一個目標函式，而理解目標函式本身也有利於我們設計學習演算法，這個會在後面具體展開。  對於tree ensemble，我們可以比較嚴格的把模型寫成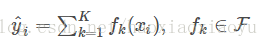：     其中每個  是一個在函式空間[6]裡面的函式，而對應了所有regression tree的集合。我們設計的目標函式也需要遵循前面的主要原則，包含兩部分 

iii. 模型學習：additive training    其中第一部分是訓練誤差，也就是大家相對比較熟悉的，如平方誤差, logistic loss等。而第二部分是每棵樹的複雜度的和，這個在後面會繼續講到。因為現在我們的引數可以認為是在一個函式空間裡面，我們不能採用傳統的如SGD之類的演算法來學習我們的模型，因此我們會採用一種叫做additive training的方式（另外，在我個人的理解裡面[7]，boosting就是指additive training的意思）。每一次保留原來的模型不變，加入一個新的函式  到我們的模型中。 

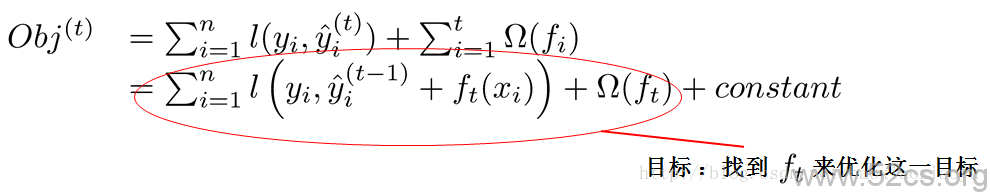
  現在還剩下一個問題，我們如何選擇每一輪加入什麼  呢？答案是非常直接的，選取一個  來使得我們的目標函式儘量最大地降低[8]。    這個公式可能有些過於抽象，我們可以考慮當  是平方誤差的情況。這個時候我們的目標可以被寫成下面這樣的二次函式[9]：    更加一般的，對於不是平方誤差的情況，我們會採用如下的泰勒展開來定義一個近似的目標函式，方便我們進行這一步的計算。    當我們把常數項移除之後，我們會發現如下一個比較統一的目標函式。這一個目標函式有一個非常明顯的特點，它只依賴於每個資料點的在誤差函式上的一階導數和二階導數[10]（注意求偏導的物件！）。有人可能會問，這個材料似乎比我們之前學過的決策樹學習難懂。為什麼要花這麼多力氣來做推導呢？    因為這樣做使得我們可以很清楚地理解整個目標是什麼，並且一步一步推匯出如何進行樹的學習。這一個抽象的形式對於實現機器學習工具也是非常有幫助的。傳統的GBDT可能大家可以理解為如優化殘差，但是這樣一個形式包含可所有可以求導的目標函式。也就是說有了這個形式，我們寫出來的程式碼可以用來求解包括迴歸，分類和排序的各種問題，正式的推導可以使得機器學習的工具更加一般。

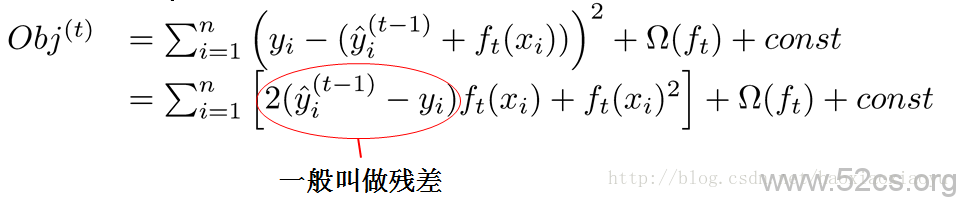
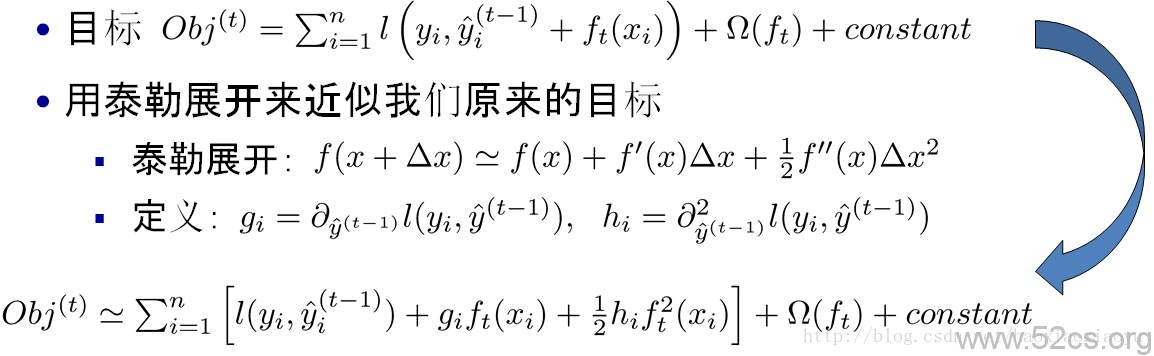
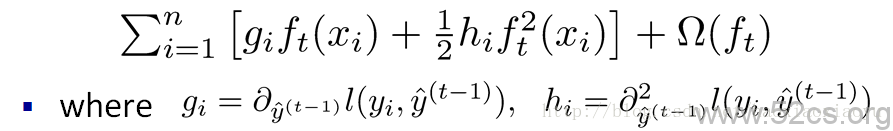
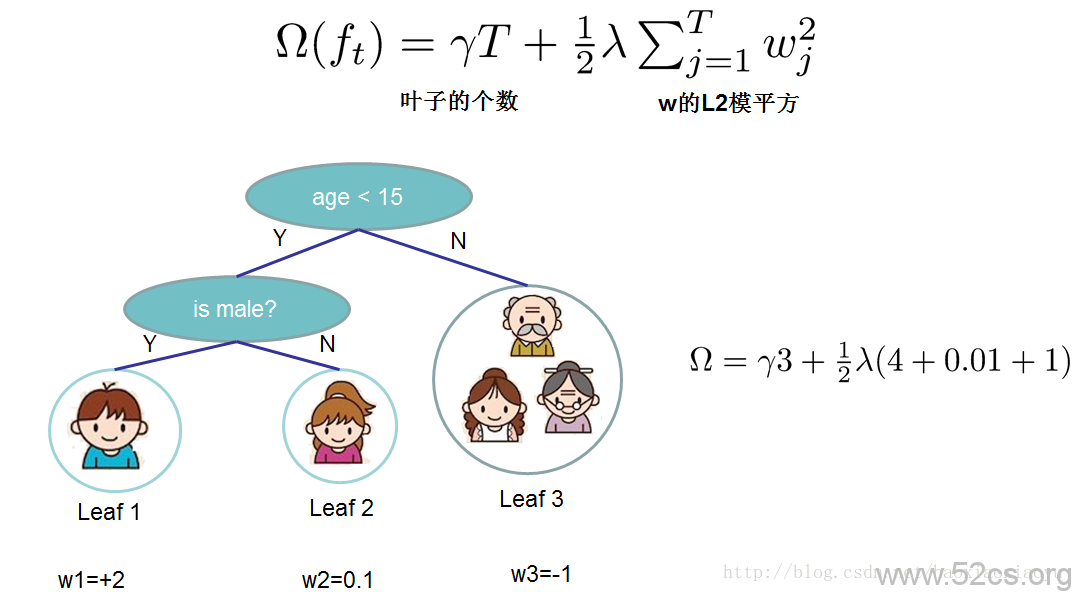
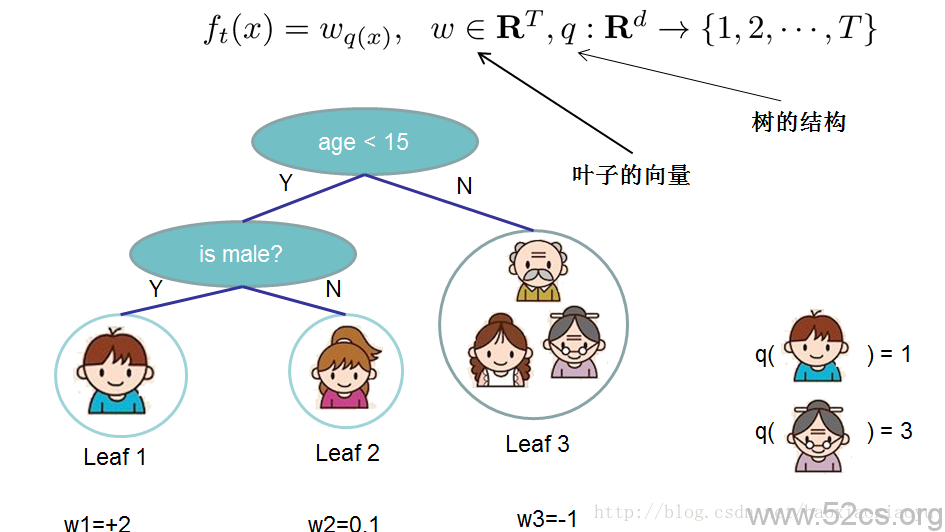
iv. 樹的複雜度    到目前為止我們討論了目標函式中訓練誤差的部分。接下來我們討論如何定義樹的複雜度。我們先對的定義做一下細化，把樹拆分成結構部分  和葉子權重部分  。下圖是一個具體的例子。結構函式  把輸入對映到葉子的索引號上面去，而  給定了每個索引號對應的葉子分數是什麼。    當我們給定了如上定義之後，可以定義一棵樹的複雜度如下。這個複雜度包含了一棵樹裡面節點的個數，以及每個樹葉子節點上面輸出分數的L2模平方。當然這不是唯一的一種定義方式，不過這一定義方式學習出的樹效果一般都比較不錯。下圖還給出了複雜度計算的一個例子。 

v. 關鍵步驟    接下來是最關鍵的一步，在這種新的定義下，我們可以把目標函式進行如下改寫，其中被定義為每個葉子上面樣本的集合 

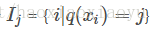
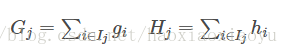
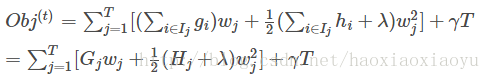
  這一個目標包含了  個相互獨立的單變數二次函式。我們可以定義    那麼這個目標函式可以進一步改寫成如下的形式，假設我們已經知道樹的結構 ，我們可以通過這個目標函式來求解出最好的，以及最好的對應的目標函式最大的增益     這兩個的結果對應如下，左邊是最好的，右邊是這個對應的目標函式的值。到這裡大家可能會覺得這個推導略複雜。其實這裡只涉及到了如何求一個一維二次函式的最小值的問題[12]。如果覺得沒有理解不妨再仔細琢磨一下 

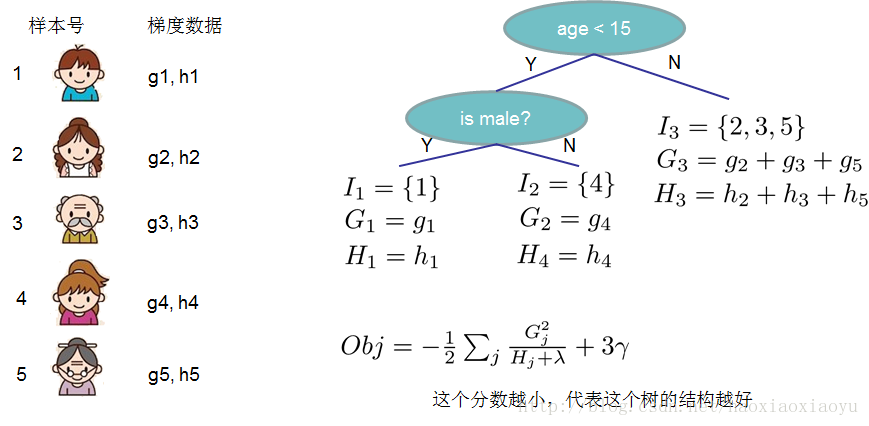
vi. 打分函式計算舉例    Obj代表了當我們指定一個樹的結構的時候，我們在目標上面最多減少多少。我們可以把它叫做結構分數(structure score)。你可以認為這個就是類似吉尼係數一樣更加一般的對於樹結構進行打分的函式。下面是一個具體的打分函式計算的例子 

vii. 列舉所有不同樹結構的貪心法    所以我們的演算法也很簡單，我們不斷地列舉不同樹的結構，利用這個打分函式來尋找出一個最優結構的樹，加入到我們的模型中，再重複這樣的操作。不過列舉所有樹結構這個操作不太可行，所以常用的方法是貪心法，每一次嘗試去對已有的葉子加入一個分割。對於一個具體的分割方案，可以獲得的增益可以由如下公式計算     對於每次擴充套件，我們還是要列舉所有可能的分割方案，如何高效地列舉所有的分割呢？我假設我們要列舉所有 x小於a 這樣的條件，對於某個特定的分割a我們要計算a左邊和右邊的導數和。     可以發現對於所有的a，只要做一遍從左到右的掃描就可以枚舉出所有分割的梯度 和 。然後用上面的公式計算每個分割方案的分數就可以了。

  觀察這個目標函式，大家會發現第二個值得注意的事情就是引入分割不一定會使得情況變好。因為我們有一個引入新葉子的懲罰項，優化這個目標對應了樹的剪枝， 當引入的分割帶來的增益小於一個閥值的時候，我們可以剪掉這個分割。大家可以發現，當我們正式地推導目標的時候，像計算分數和剪枝這樣的策略都會自然地出現，而不再是一種因為heuristic而進行的操作了。

  講到這裡文章進入了尾聲，雖然有些長，希望對大家有所幫助，這篇文章介紹瞭如何通過目標函式優化的方法比較嚴格地推匯出boosted tree的學習。因為有這樣一般的推導，得到的演算法可以直接應用到迴歸、分類、排序等各個應用場景中去。

5. 尾聲：xgboost    這篇文章講的所有推導和技術都指導了xgboost https://github.com/dmlc/xgboost 的設計。xgboost是大規模並行boosted tree的工具，它是目前最快最好的開源boosted tree工具包，比常見的工具包快10倍以上。在資料科學方面，有大量kaggle選手選用它進行資料探勘比賽，其中包括兩個以上kaggle比賽的奪冠方案。在工業界方面，xgboost的分散式版本有廣泛的可移植性，支援在YARN, MPI, Sungrid Engine等各個平臺上面執行，並且保留了單機並行版本的各種優化，使得它可以很好地解決工業界大規模的問題。有興趣的同學可以嘗試使用一下，也歡迎貢獻程式碼。

註解和連結：

1: Multiple Additive Regression Trees, Jerry Friedman, KDD 2002 Innovation Award 創新獎 http://www.sigkdd.org/node/362  2: Introduction to Boosted Trees, Tianqi Chen  , 2014 http://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf  3: Principles of Data Mining, David Hand et al,2001. Chapter 1.5 Components of Data Mining Algorithms, 將資料探勘演算法解構為四個元件：1）模型結構（函式形式，如線性模型），2）評分函式（評估模型擬合數據的質量，如似然函式，誤差平方和，誤分類率），3）優化和搜尋方法（評分函式的優化和模型引數的求解），4）資料管理策略（優化和搜尋時對資料的高效訪問）。  4: 在概率統計中，引數估計量的評選標準有三：1）無偏性（引數估計量的均值等於引數的真實值），2）有效性（引數估計量的方差越小越好），3）一致性（當樣本數從有限個逐漸增加到無窮多個時，引數估計量依概率收斂於引數真值）。《概率論與數理統計》，高祖新等，1999年，7.3節估計量的評選標準  5: Breiman, L., Friedman, J., Stone, C. J., & Olshen, R. A. (1984). Classification and regression trees. CRC press. Breiman獲KDD 2005 Innovation Award 創新獎  6: F是泛函空間，或者叫假設空間；f是函式，或者叫假設。這裡的ensemble一共有K個元件/基學習器，他們的組合方式是不帶權重的累加。NOTE：【一般boosting裡面（如AdaBoost）f是有權重疊加 原因是那些權重自然地被吸收到葉子的weight裡面去了。】 by Chen Tianqi  7: Friedman等（ Friedman, J., Hastie, T., & Tibshirani, R. (2000). Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). The annals of statistics, 28(2), 337-407. ）在2000年為boosting這種整合學習方法正規化提供了一種統計解釋，即加性邏輯斯蒂迴歸。但是他們不能完全解釋AdaBoost演算法的抗過擬合性。南大周志華等人（http://www.slideshare.net/hustwj/ccl2014-keynote）從統計學習理論的間隔分佈出發，較完滿的解決了這個問題。  8: 這個思想即是AdaBoost等boosting演算法的思想：序列生成一系列基學習器，使得當前基學習器都重點關注以前所有學習器犯錯誤的那些資料樣本，如此達到提升的效果。  9: 注意，這裡的優化搜尋變數是f（即搜尋當前的基學習器f），所以其他不關於ff的項都被吸納到const中，如當前的誤差損失  10: 1). 分別作為要優化的變數f的一次係數gg和二次係數1/2∗h1/2∗h  2). 誤差函式對 y^(t−1)iy^i(t−1)求導時，即涉及到前t−1t−1個基學習器，因為他們決定了當前的預測結果  11: 因為每個資料點落入且僅落入一個葉子節點，所以可以把nn個數據點按葉子成組，類似於合併同類項，兩個資料點同類指的是落入相同的葉子，即這裡的指示變數集IjIj  12: 變數是wj，關於它的二次函式是：Gj∗wj+1/2(Hj+λ)∗w2jGj∗wj+1/2(Hj+λ)∗wj2，該函式對變數wjwj求導並令其等於0，即得到wj的表示式。