吳恩達機器學習個人筆記(九)-異常檢測

阿新 • • 發佈：2018-12-21

異常檢測也屬於無監督學習,但是看起來又有點像是監督學習，其實異常檢測依靠個人理解為如果有一堆資料聚集在一個範圍內，這個範圍內的資料都為正常(相比較與異常)，如果新輸入一個數據，即要檢測該資料是否處於該範圍內。屬於正常的資料或者異常，所以叫做異常檢測。

1 問題的動機(Problem Motivation)

什麼是異常檢測(Anomaly detection）,吳恩達老師給大家舉了一個例子是關於飛機引擎QA的:

假設飛機引擎製造商為了測試飛機引擎，測量了關於引擎的一些變數，比如熱量，振動等，將他們作為特徵:

那麼你就有一個數據集，從 $x^{(1)}$ 到 $x^{(m)}$ ,將這些資料製成表格。看起來如下所示

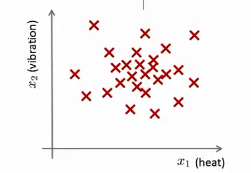
上圖中的每個×都表示一個數據，也就是飛機的引擎，這些都是無標籤的資料。這樣異常檢測的問題即可定義如下:假設生產出一個新的飛機引擎，假設為 $x_{test}$ 。那麼異常檢測就是檢視該新生產的引擎是否正常。

由此可以引出下面的定義。給定一個數據集 $x^{(1)},x^{(2)},\cdots ,x^{(m)}$ ,我們假設資料集是正常的，希望知道新的資料 $x_{test}$ 是不是異常的，即這個測試資料不屬於該資料的機率如何。我們所構建的模型應該可以得出該新資料屬於一個數據集的可能性 $p(x)$ 是多少。

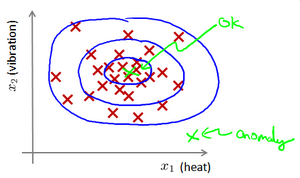
上圖中，藍色圈內的資料屬於該資料集的可能性比較高，而越是偏遠的資料，資料該資料集的可能性就越低。這種方法被稱為密度估計，表達如下:

$p(x)\left\{\begin{matrix} < \varepsilon & anomaly\\ \geq \varepsilon & normal \end{matrix}\right.$

模型 $p(x)$ 為我們其屬於一組資料的可能性，通過 $p(x)<\varepsilon$ 來檢測非正常使用者

2 高斯分佈(Gaussian Distribution )

該部分只是對高斯分佈的介紹，因為該高斯分佈對其演算法異常重要。高斯分佈也叫做正態分佈

如果我們認為變數 $x$ 符合高斯分佈 $x\sim N(\mu ,\sigma^{2})$ ，那麼其概率密度函式為: $p(x,\mu ,\sigma ^{2}) =\frac{1}{\sqrt{2\pi \sigma }} exp(-\frac{(x-\mu )^{2}}{2\sigma ^{2}})$

我們可以用已有的資料來預測總體中的 $\mu$ 和 $\sigma ^{2}$ 的計算方法如下:

$\mu =\frac{1}{m}\sum _{i=1}^{m}x^{(i)}$ $\sigma ^{2}=\frac{1}{m}\sum _{i=1}^{m}(x^{(i)}-\mu )^{2}$

高斯分佈的樣例如下所示

3 演算法（Algorithm）

異常檢查演算法為：對於給定的資料集 $x^{(1)},x^{(2)},\cdots ,x^{(m)}$ ，我們要針對每一個特徵計算 $\mu$ 和 $\sigma ^{2}$ 的估計值

$\mu_{j} =\frac{1}{m}\sum _{i=1}^{m}x_{j}^{(i)}$ $\sigma _{j}^{2}=\frac{1}{m}\sum _{i=1}^{m}(x_{j}^{(i)}-\mu_{j} )^{2}$

一旦我們獲得了平均值和方差的估計值，給定一個新的一個訓練例項，即可根據模型計算 $p(x)$ :

$p(x)=\prod _{j=1}^{n}p(x_{j};\mu _{j},\sigma _{j}^2)=\prod _{j=1}^{n}\frac{1}{\sqrt{2\pi \sigma _{j}}}exp(-\frac{(x_{j}-\mu _{j})^{2}}{2\sigma _{j}^{2}})$

當 $p(x)<\varepsilon$ 時為異常。下圖為一個數據又兩個特徵的訓練集，以及特徵的分佈情況:

$x_{1}$ 也就是特徵1的高斯分佈如第一張圖所示， $x_{2}$ 也就是特徵2 的高斯分佈如圖2所示。下面有一個三維圖表示的時密度估計函式， $z$ 軸為根據兩個特徵的值 $x_{1}$ 和 $x_{2}$ 所估計的 $p(x)$ 值:

我們選擇一個 $\varepsilon$ ，將 $p(x)=\varepsilon$ 作為我們的判定邊界，當 $p(x)>\varepsilon$ 時預測資料為正常資料，否則為異常

4 開發和評價一個異常檢測系統(Developing and Evaluating )

異常檢測演算法是一個非監督學習演算法，意味著我們無法根據結果變數 $y$ 的值來告訴我們資料是否真的是異常的。我們需要另一種方法來檢驗演算法是否有效。

當我們開發一個異常檢測系統時，我們從帶標記（異常或正常）的資料著手，我們從其中選擇一部分正常資料用於構建訓練集，然後用剩下的正常資料和異常資料混合的資料構成交叉檢驗集和測試集。

例如：我們有10000臺正常引擎的資料，有20臺異常引擎的資料。我們這樣分配資料：

6000臺正常引擎的資料作為訓練集

2000臺正常引擎和10臺異常引擎的資料作為交叉檢驗集

2000臺正常引擎和10臺異常引擎的資料作為測試集

具體的評價方法如下：

根據測試集資料，我們估計特徵的平均值和方差並構建 $p(x)$ 函式
對交叉檢驗集，我們嘗試使用不同的 $\varepsilon$ 值作為閥值，並預測資料是否異常，根據F1值或者查準率與查全率的比例來選擇 $\varepsilon$
選出 $\varepsilon$ 後，針對測試集進行預測，計算異常檢驗系統的值，或者查準率與查全率之比

5異常檢測與監督學習對比

之前構建的異常檢測系統也使用了帶標籤的資料，與監督學習很相似。下面對兩種機器學習方法進行比較:

異常檢測	監督學習
非常少量的正向類( $y=1$ )，大量的負向類（ $y=0$ ）	同時有大量的正向類和負向類
由許多不同種類的異常。不能根據非常少量的正向類來訓練演算法	有足夠多的正向類例項，足夠用於訓練演算法，未來遇到的正向類例項可能與訓練集中的非常相近
未來遇到的異常可能與已掌握的異常非常的不同
例如:欺騙行為檢測，生產(例如飛機引擎)	例如;郵件過濾器，天氣預報腫瘤分類

我感覺異常檢測與監督學習的選擇為他們之間用來訓練模型的資料集之間的差異，異常檢測演算法中兩個型別的資料集可以說時不對等的，其中一方比較多，另一方很少的量。而監督學習可能兩個型別的資料都一樣的多，都可以用來訓練。

6 選擇特徵

對於異常檢測演算法，我們使用的特徵非常的重要。我們之前假設我們選擇的特徵都是符合高斯分佈的，如果資料的分佈不是高斯分佈，那異常檢測演算法也能夠工作，最主要的是我們可以將資料轉化為高斯分佈。例如使用對數函式 $x=log(x+c)$ ,其中 $c$ 為非負常數；或者 $x=x^{c}$ ，c為 $0\sim 1$ 之間的一個分數。例如下圖所示

選擇特徵通俗的來講就是可能我們特徵分佈不是高斯分佈，我們通過一些方法將這些特徵變成高斯分佈

7 多元高斯分佈

假設我們有兩個相關的特徵，並且這兩個特徵的值域範圍比較寬，這種情況下，一般的高斯分佈模型可能不能很好的識別異常資料。通俗化就是兩個特獲的正常取值範圍都比較大，新資料的兩個特徵取值都符合之前的範圍，但是綜合起來就不符合，為異常。這種原因是，一般的高斯分佈模型嘗試的是去同時抓住兩個特徵的偏差，因此創造出一個比較大的判定邊界。

下圖中是兩個相關的特徵，洋紅色的線是一般的高斯分佈模型獲得的判定邊界，很明顯綠色所代表的X一個異常的資料，但是其 $p(x)$ 的值仍然處於正常範圍內。如果使用多元高斯分佈模型，那麼會建立像圖中藍色曲線所代表的判定邊界。

一般的高斯分佈模型中，我們計算 $p(x)$ 的方法是:通過分別計算每個特徵對應的機率然後將其累乘起來。在多元高斯分佈模型中，我們將構建特徵的協方差矩陣，用所有的特徵一起來計算 $p(x)$ .

一開始我們先計算所有特徵的平均值，然後再計算協方差矩陣

$p(x)=\prod _{j=1}^{n}p(x_{i};\mu ,\sigma _{j}^{2})=\prod _{j=1}^{n}\frac{1}{\sqrt{2\pi \sigma _{j}}}exp(-\frac{(x_{j}-\mu _{j})^{2}}{2\sigma _{j}^2})$

$\mu =\frac{1}{m}\sum _{i=1}^{m}x^{(i)}$

$\Sigma =\frac{1}{m}\sum_{i=1}^{m}(x^{(i)}-\mu )(x^{(i)}-\mu )^{T}=\frac{1}{m}(X-\mu )^{T}(X-\mu )$

其中 $\mu$ 是一個向量，其每一個單元都是原特徵矩陣中每一行資料的均值，最後我們可以利用上述所計算的 $\mu$ 和 $\Sigma$ 來計算之前的高斯分佈公式的 $p(x)$ ,如下所示

$p(x)=\frac{1}{(2\pi )^{2}\left | \Sigma \right |^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu )^{T}\Sigma ^{-1}(x-\mu ))$

其中 $\left | \Sigma \right |$ 為定矩陣， $\Sigma ^{-1}$ 為逆矩陣。為啥要使用協方差，協方差矩陣對模型的影響如下所示:

由上圖可以看出，不斷改變協方差矩陣中的值，高斯分佈的模型的變化也不盡相同。上圖中的5個不同模型，從左往右依次是

1.是一個一般的高斯分佈模型

2.通過協方差矩陣，令特徵1擁有較小的偏差，同時保持特徵2的偏差

3.通過協方差矩陣，令特徵2擁有較大的偏差，同時保持特徵1的偏差

4.通過協方差矩陣，在不改變兩個特徵的原有偏差的基礎上，增加兩者之間的正相關性

5.通過協方差矩陣，在不改變兩個特徵的原有偏差的基礎上，增加兩者之間的負相關性

吳恩達機器學習個人筆記(九)-異常檢測

1 問題的動機(Problem Motivation)

2 高斯分佈(Gaussian Distribution )

3 演算法（Algorithm）

4 開發和評價一個異常檢測系統(Developing and Evaluating )

5異常檢測與監督學習對比

6 選擇特徵

7 多元高斯分佈

吳恩達機器學習個人筆記(九)-異常檢測

吳恩達機器學習個人筆記(七)-聚類

吳恩達機器學習（第九章）---神經網路

吳恩達機器學習視訊筆記03——矩陣和向量

吳恩達機器學習課程筆記02——處理房價預測問題（梯度下降演算法詳解）

吳恩達機器學習視訊筆記——簡單知識背景

吳恩達機器學習視訊筆記——梯度下降簡化技巧

機器學習筆記（參考吳恩達機器學習視訊筆記）16_決策樹

機器學習筆記（參考吳恩達機器學習視訊筆記）15_推薦系統

機器學習筆記（參考吳恩達機器學習視訊筆記）14_異常檢測

機器學習筆記（參考吳恩達機器學習視訊筆記）13_降維

機器學習筆記（參考吳恩達機器學習視訊筆記）12_聚類

機器學習筆記（參考吳恩達機器學習視訊筆記）11_支援向量機

機器學習筆記（參考吳恩達機器學習視訊筆記）10_機器學習系統的設計

機器學習筆記（參考吳恩達機器學習視訊筆記）09_應用機器學習的建議

機器學習筆記（參考吳恩達機器學習視訊筆記）08_神經網路的學習

機器學習筆記（參考吳恩達機器學習視訊筆記）07_神經網路介紹

機器學習筆記（參考吳恩達機器學習視訊筆記）06_正則化

機器學習筆記（參考吳恩達機器學習視訊筆記）04_多變數線性迴歸

吳恩達機器學習課程筆記章節二單變數線性迴歸

吳恩達機器學習個人筆記(九)-異常檢測

1 問題的動機(Problem Motivation)

2 高斯分佈(Gaussian Distribution )

3 演算法（Algorithm）

4 開發和評價一個異常檢測系統(Developing and Evaluating )

5異常檢測與監督學習對比

6 選擇特徵

7 多元高斯分佈

相關推薦