題目
知識點： 二分、樹、貪心
講解：
對於這一題在考場上是一臉懵逼，先理解一下題目吧。
給你一個數要求你從這個樹上摳出m條鏈，要求：最小的鏈最長
這個題目最大的困難是怎麼摳？
首先想到的就是二分，為什麼？最小的鏈最長不就是二分的經典句子嘛。
所以我們考慮二分最小鏈的長度，可是還是那個問題怎麼摳？
我們在沒思路的時候我們可以看看可不可以拿部分分，說不定打著打著就有思路了 （博主本人） 。

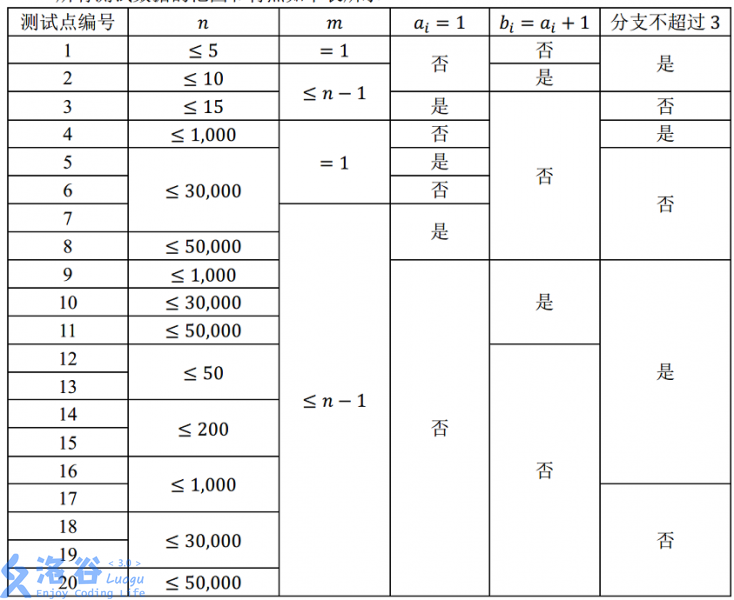
根據資料我們可以分成三類，一類是bi=ai+1，這個其實就是一條鏈，還有ai=1，這個是本題最噁心的菊花圖，還有分枝不超過3，這個其實就是正解的弱化版，我就是打這個然後想出正解的。
我們先考慮鏈的時候怎麼辦？

bool check(int mid)
{
	num=0,much=0;//num為目前鏈的長度，much為目前已經摳到much條了 
	for(int i=1;圖還沒遍歷完;i=v)//v是i的兒子
	{
		num+=u;//u是這條邊的邊權
		if(num>=mid)
			num=0,much++; 
	}
	if(much>=m)//我們要摳m條，判斷數否可以摳到 
		return true;
	else return
 
 false;
}
int l=0,r=inf,ans=0;//inf為極大值
while(l<=r)
{
	int mid=(l+r)>>1;
	if(check(mid))
	{
		ans=mid;
		l=mid+1;
	}
	r=mid-1;
}
printf("%d",ans);

接下來是菊花圖：
菊花圖也就是所有的點有且僅和1這個點相連，因為長得像菊花，所以叫菊花圖。
我們可以發現，根據題目，在菊花圖上符合條件的鏈要麼由本身組成，要麼由兩條鏈組成，所以根據貪心，我們先把所有的邊權按從大到小排序，設邊權陣列為a，然後我們再找到m條鏈（根據貪心大鏈配小鏈，兩個比一個優），所以我們可以得出答案為a[1]+a[2 * m]、a[2]+a[2 * m-1] ······ 中最小的，所以我們可以得出菊花圖的解法。
程式碼：

bool cmp1(int x,int y)//從大到小排 
{
	return x>y;
}
ans=inf;//先給答案付個極大值 
sort(a+1,a+n,cmp1);//排序 
for(int i=1;i<=m;i++)
	ans=min(ans,a[i]+a[2*m-i+1]);//找答案 

然後是分枝不超過三：
這句話的意思就是樹上的任意一個節點它的兒子最多兩個，這意味著什麼？ （不知道）
我們分析一下性質，對於一棵樹中的任意一個節點（把個體先分析）我們可以知道摳鏈要麼是直接在內部兩個兒子通過父親相連拼接成一條鏈，要麼就是通過父親到達祖先和祖先拼接（根據貪心我們可以知道，如果有很多鏈都需要和祖先連線，那麼我們選的一定是最長的一條）。
我們先考慮內部連線：
我們直接開個陣列存兒子中需要和祖先連線的最長鏈，然後再兩兩連線看是不是可以滿足大於等於mid，如果可以根據貪心一定是要剛剛好，即與之配對的一定是可以配對中最小的，這樣我們才可以儘可能地留下大的與祖先配對。
考慮與祖先連線：
我們直接開一個數組dp，dp[i]表示i這個節點中要與祖先配對的不符合條件（條件就是兩兩內部拼接不成功的那些鏈）的鏈中最長的，在後面直接呼叫就好了。
總結：
這樣我們就考慮完了，因為兒子最多兩個，所以內部拼接時要麼這兩個連線，要麼選擇最大的去和祖先連線。
那麼對於不是最多兩個兒子的解呢？
我們從小到大把兒子中要與祖先配對的鏈長度排序（就是dp數組裡的東西），從最小的鏈去找到最小的可以和它匹配的鏈（這個也是二分），然後如果沒有邊可以和它匹配或者只剩一條邊了我們就把它存入dp中與祖先匹配（注意要比較選最大）。
這樣這一題就解決了。
可是測時我們發現有幾個點TLE，正常，這就是我說的這一題的坑點，菊花圖！
我們這個的做法是O（n ^ 2 log n）的，（n表示一個節點兒子的個數），所以對於兒子的分佈越平均越快，可菊花圖就是最不平均的，怎麼辦呢？
其實我們直接特判一下，如果是菊花圖直接用上面說的對於菊花圖的做法，其他的用我們的正解就好了。
注意：
要用不定長陣列vector來存兒子中要與祖先匹配的鏈的長度，否則會MLE（爆記憶體）！
程式碼：

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,head[100100],Next[100100],ver[100100],edge[100100],size=0,much=0,dp[50100],a[100100];
inline int read()//快讀 
{
	char ch;
	while(ch=getchar(),ch<'0' || ch>'9');
	int num=ch-'0';
	while(ch=getchar(),ch>='0' && ch<='9')
		num=(num<<3)+(num<<1)+ch-'0';
	return num;
}
bool cmp(int x,int y)//從小到大排序 
{
	return x<y;
}
void add(int x,int y,int u)//邊表嘗龜操作 
{
	size++;
	Next[size]=head[x];
	head[x]=size;
	ver[size]=y;
	edge[size]=u;
	return ;
}
inline void dfs(int x,int fa,int need)
{
	vector <int> q;//用不定常陣列 
	for(int i=head[x];i;i=Next[i])//遍歷一下 
	{
		int y=ver[i],u=edge[i];
		if(y==fa)
			continue;
		dfs(y,x,need);
		q.push_back(dp[y]+u);//把兒子需要和祖先匹配的鏈存下來，記得加上這條邊的權值 
	}
	sort(q.begin(),q.end(),cmp);//排序 
	while(q.size() && q[q.size()-1]>=need)//從大到小判斷是否有不用和別人匹配就滿足條件的 
	{
		much++;
		q.pop_back();//刪除 
	}
	while(q.size()>=2)//有兩條鏈即以上的 
	{
		if(q[0]+q[q.size()-1]>=need)//判斷是否可以合併，如果連和最大值合併都沒有用，那肯定不可以 
		{
			int l=0,r=q.size(),ans=-1;
			while(l<=r)//二分找最小的 
			{
				int mid=(l+r)>>1;
				if(q[mid]+q[0]>=need && mid!=0)
					ans=mid,r=mid-1;
				else l=mid+1;
			}
			much++;
			q.erase(q.begin()+ans);//刪除 
			q.erase(q.begin());//刪除 
		}
		if(q.size() && q[0]+q[q.size()-1]<need)//如果最大值都無法與它匹配，直接存入dp陣列 
		{
			dp[x]=max(dp[x],q[0]);//比較大小 
			q.erase(q.begin());//刪除 
		}
	}
	if(q.size())//還有一條邊的話 
	{
		dp[x]=max(dp[x],q[q.size()-1]);//直接存入dp 
		q.pop_back();//刪除 
	}
}
inline bool check(int mid)//check函式，inline不用管它，可有可沒有，只是加了會稍微快點，這道題不影響 
{
	for(int i=1;i<=n;i++)//初始化 
		dp[i]=0;
	much=0;//初始化 
	dfs(1,0,mid);//爆搜整棵樹 
	if(much>=m)//判斷是否可以摳出m條鏈 
		return true;
	else return false;
}
bool cmp1(int x,int y)//從大到小排序 
{
	return x>y;
}
int main()
{
	int l=0,r,ans=0,sum=0,bj=1;//l，r表示二分邊界，ans是答案，sum是所有邊權的和，我們通過它計算極大值，bj判斷是否是菊花圖 
	n=read();
	m=read();
	for(int i=1;i<n;i++)
	{
		int x,y,u;
		x=read();
		y=read();
		u=read();
		a[i]=u;//如果是菊花圖我們要用到所有邊權所以記下來 
		if(x!=1)//判斷是否是菊花圖 
			bj=0;
		sum+=u;//計算sum 
		add(x,y,u);
		add(y,x,u);
	}
	r=sum/m+1;//計算極大值並且賦給r 
	if(bj)//是菊花圖 
	{
		ans=sum;//先給答案付個極大值 
		sort(a+1,a+n,cmp1);//排序 
		for(int i=1;i<=m;i++)
			ans=min(ans,a[i]+a[2*m-i+1]);//找答案 
	}
	else //否則 
	{
		while(l<=r)//二分 
		{
			int mid=(l+r)>>1;
			if(check(mid))//check，二分嘗龜 
			{
				ans=mid;//記錄答案 
				l=mid+1;//調整邊界 
			}
			else r=mid-1;
		}
	}
	printf("%d",ans);//輸出答案 
	return 0;
}

這一題因為有不定長陣列比較難除錯，很可能會越界，所以要時刻注意陣列大小。
如果有看不懂的歡迎留言。