[multiset][貪心]NOIP2018 TG T1 賽道修建
題目描述
C 城將要舉辦一系列的賽車比賽。在比賽前,需要在城內修建 m 條賽道。
C 城一共有 nn 個路口,這些路口編號為1,2,…,n,有 n−1 條適合於修建賽道的雙向通行的道路,每條道路連線著兩個路口。其中,第 i 條道路連線的兩個路口編號為 ai 和 bi,該道路的長度為 li。藉助這 n−1 條道路,從任何一個路口出發都能到達其他所有的路口。
一條賽道是一組互不相同的道路 e1,e2,…,ek,滿足可以從某個路口出發,依次經過 道路 e1,e2,…,ek(每條道路經過一次,不允許調頭)到達另一個路口。一條賽道的長度等於經過的各道路的長度之和。為保證安全,要求每條道路至多被一條賽道經過。
目前賽道修建的方案尚未確定。你的任務是設計一種賽道修建的方案,使得修建的 mm 條賽道中長度最小的賽道長度最大(即 m 條賽道中最短賽道的長度儘可能大)
輸入輸出格式
輸入格式:
輸入檔案第一行包含兩個由空格分隔的正整數 n,m,分別表示路口數及需要修建的 賽道數。
接下來 n-1 行,第 ii 行包含三個正整數 ai,bi,li,表示第 i 條適合於修建賽道的道 路連線的兩個路口編號及道路長度。保證任意兩個路口均可通過這 n−1 條道路相互到達。每行中相鄰兩數之間均由一個空格分隔。
輸出格式:
輸出共一行,包含一個整數,表示長度最小的賽道長度的最大值。
輸入輸出樣例
輸入樣例#1:7 1 1 2 10 1 3 5 2 4 9 2 5 8 3 6 6 3 7 7輸出樣例#1:
31輸入樣例#2:
9 3 1 2 6 2 3 3 3 4 5 4 5 10 6 2 4 7 2 9 8 4 7 9 4 4輸出樣例#2:
15
說明
【輸入輸出樣例 1 說明】
所有路口及適合於修建賽道的道路如下圖所示: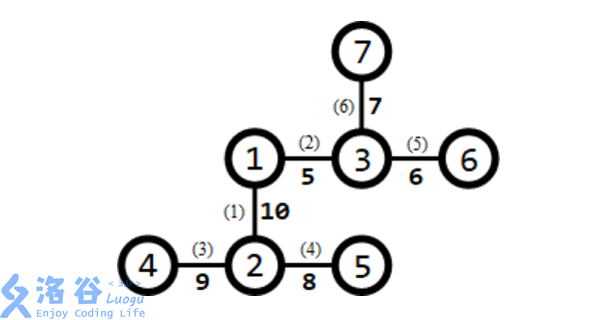
道路旁括號內的數字表示道路的編號,非括號內的數字表示道路長度。 需要修建 1 條賽道。可以修建經過第 3,1,2,6 條道路的賽道(從路口 4 到路口 7), 則該賽道的長度為 9 + 10 + 5 + 7 = 31,為所有方案中的最大值。
【輸入輸出樣例 2 說明】
所有路口及適合於修建賽道的道路如下圖所示: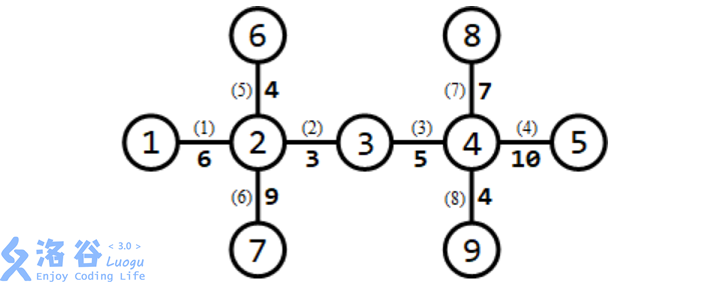
需要修建 3條賽道。可以修建如下 3條賽道:
- 經過第 1,6條道路的賽道(從路口 1 到路口7),長度為 6 + 9 = 15;
- 經過第5,2,3,8 條道路的賽道(從路口6 到路口 9),長度為 4 + 3 + 5 + 4 = 16;
- 經過第 7,4 條道路的賽道(從路口 8 到路口5),長度為 7 + 10 = 17。 長度最小的賽道長度為 15,為所有方案中的最大值。
【資料規模與約定】
所有測試資料的範圍和特點如下表所示 :
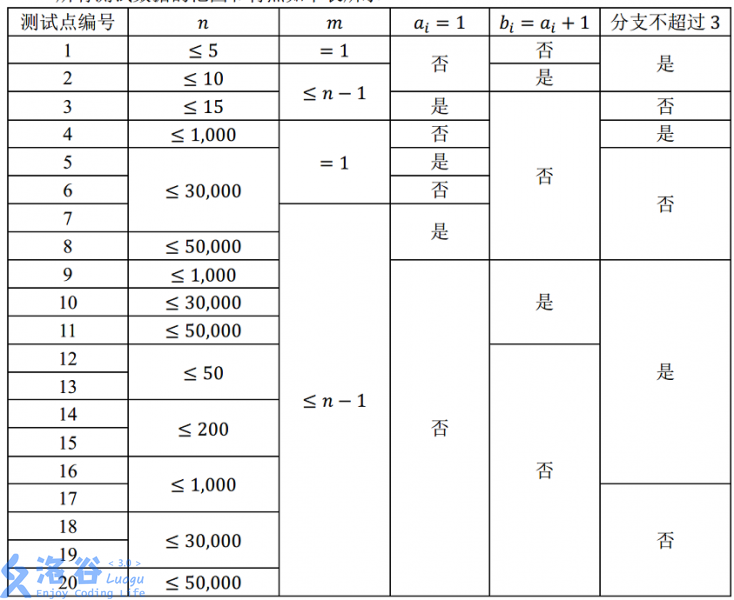
其中,“分支不超過 3”的含義為:每個路口至多有 3 條道路與其相連。 對於所有的資料, 2 ≤ n ≤ 50,000, 1 ≤ m ≤ n-1, 1≤ai,bi≤n,1≤li≤10,000。
分析
其實這道題挺簡單的(果然是我太菜了嗎……)
二分長度應該都想得到,畢竟最小值最大,二分性不說了
首先我們可以證明,如果從i出發有兩條鏈,它們的值大於等於length的話,那麼合併它們必定不虧
為什麼呢?因為這其中最多上傳一條,也就是至多貢獻1的答案,那麼顯然合併會更加優秀
那麼我們可以用f[i]表示從i出發向下所得到未被佔用的最長鏈,那麼我們用multiset存所有能夠上傳到當前點的鏈,即f[son]+w[edge]
那麼首先我們先將已經滿足要求的挑出來,答案++
然後我們從小到大列舉鏈,用lowerbound找到最合適的鏈和它匹配掉,如果找不到合適的鏈,那麼可以將這條鏈記錄為f[i](反正鏈長在multiset裡面是單調的)
然後記得清空multiset,還有multiset和儲存不能和子節點一起進行,要遍歷完子節點才能儲存鏈(因為共用一個嘛)

#include <iostream> #include <cstdio> #include <set> using namespace std; const int N=5e4+10; struct Edge { int u,v,w,nx; }g[2*N]; int cnt,list[N]; int f[N]; multiset<int> t; int n,m,lans,ans,length; void Add(int u,int v,int w) { g[++cnt]=(Edge){u,v,w,list[u]};list[u]=cnt; } void DFS(int u,int fa) { for (int i=list[u];i;i=g[i].nx) if(g[i].v!=fa) DFS(g[i].v,u); for (int i=list[u];i;i=g[i].nx) if(g[i].v!=fa) t.insert(g[i].w+f[g[i].v]); while (!t.empty()) { int ed=*t.rbegin(); if (ed>=length) lans++,t.erase(t.find(ed)); else break; } f[u]=0; while (!t.empty()) { int bg=*t.begin();t.erase(t.begin()); multiset<int>::iterator nx=t.lower_bound(length-bg); if (nx==t.end()) f[u]=bg; else t.erase(nx),lans++; } t.clear(); } bool Check(int x) { lans=0;length=x; DFS(1,0); return lans>=m; } int main() { scanf("%d%d",&n,&m); int l=2147483647,r=0; for (int i=1,u,v,w;i<n;i++) scanf("%d%d%d",&u,&v,&w),Add(u,v,w),Add(v,u,w),l=min(l,w),r+=w; int mid; while (l<=r) { mid=l+r>>1; if (Check(mid)) ans=mid,l=mid+1; else r=mid-1; } printf("%d",ans); }View Code

