1. 系統的極點和零點

傳遞函式為確定重要的系統響應特性提供了不需要求解完整的微分方程的理論。

    複數  s = ρ + jω

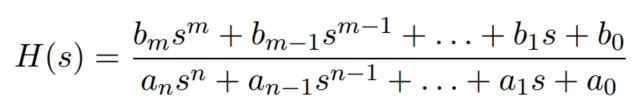
可以寫成

z1 z2...zm 為零點 H(s) -> 0

p1 p2 ...pn為極點   H(s) - > ∞

example1:

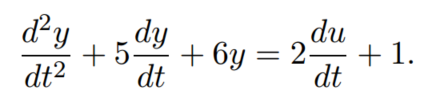
傳遞函式為
              2 s + 1
H(s) =  -------------
           s^2 + 5 s + 6

               1         s + 1/2
H(s) =    ---    ---------------------
               2      (s-（-3))(s-(-2))

零點 s = -1/2

極點 s = -3  和 s = -2

example2:

一個系統，極點為 p1 ,p2 = -1±j2  ,一個零點為 z = -4,增益 K = 3, 則 系統響應函式為：

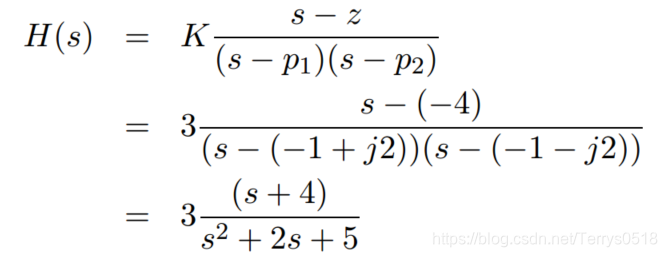
等效的微分方程

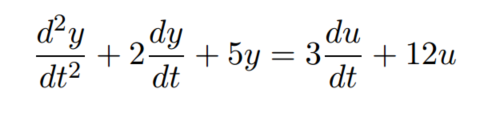
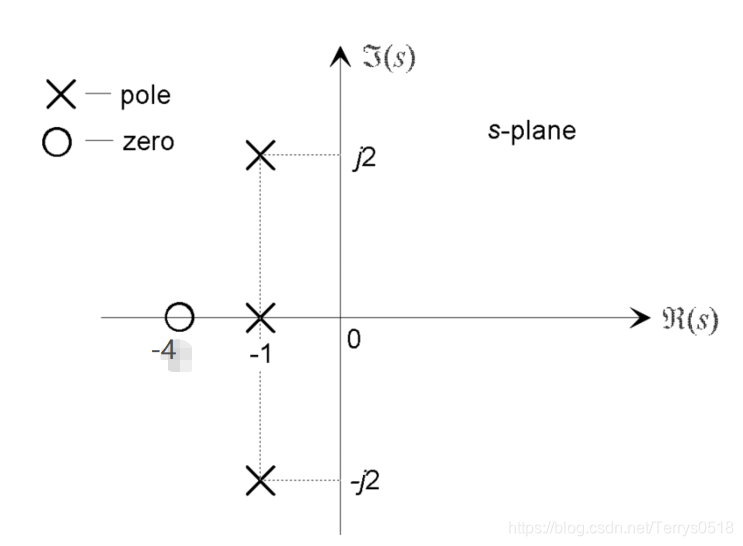
2. 傳遞函式的幾何分析

對於複數函式，可以等效為向量的表示方法

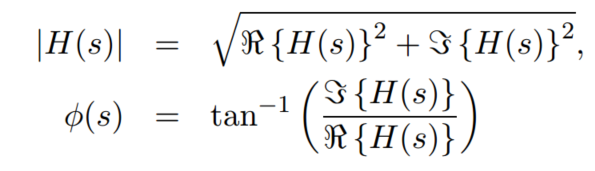
對於
 

分母的每一項，都可以表示成：

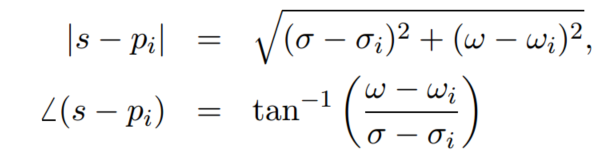
因此

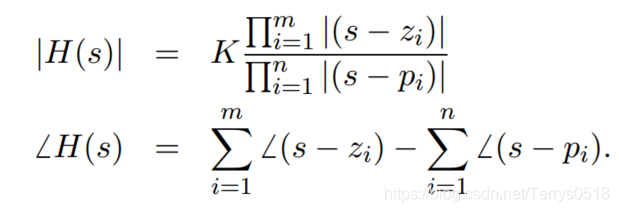
example:

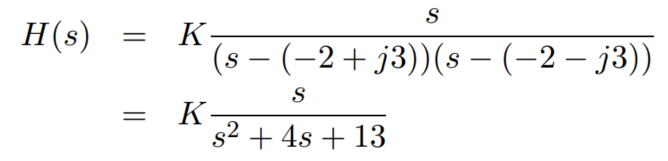
當s = 0 + j5 時

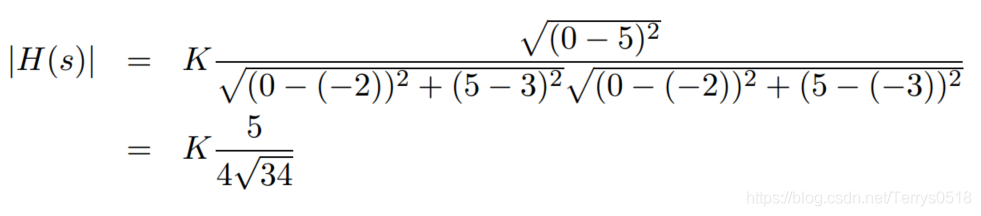
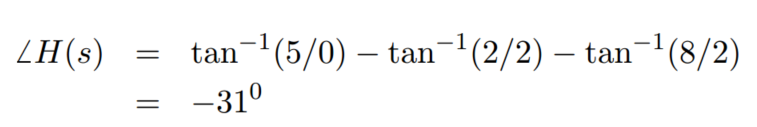
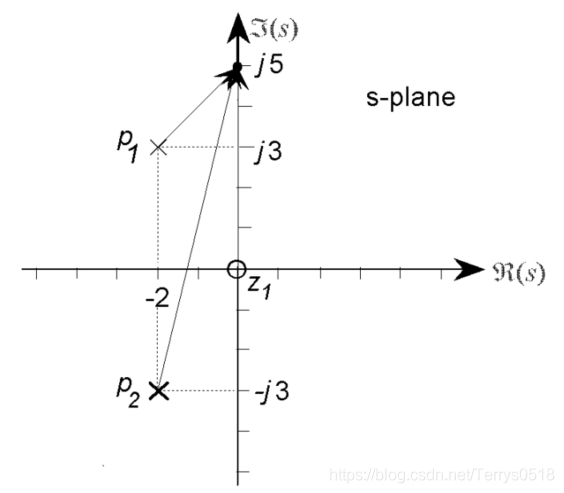
因此 傳遞函式的響應特性，可以從圖上表示出來  對某一個訊號的增益，相位的改變，都可以用作圖的方法分析，簡單又直觀。