【 MATLAB 】 WLLS algorithm Simulation of TOA
阿新 • • 發佈:2018-12-22
模擬的條件與之前講解非線性演算法之牛頓——拉夫森演算法時候的模擬條件一致。從下面的定位示意圖中也能看出來,測量站的位置以及個數,以及目標位置。
測量站的位置:x1 = [0,0];x2 = [0,10];x3 = [10,0];x4 = [10,10];
目標的真實位置:x=[2,3].
信噪比正常定義,設定為30dB,從下圖的定位示意圖中可以看出,基本可以定位,因為估計出來的目標位置與目標真實位置基本重合,但存在一定的誤差。這就要求我們去分析誤差,看看什麼樣的誤差我們能夠接受,對應的信噪比是多少?

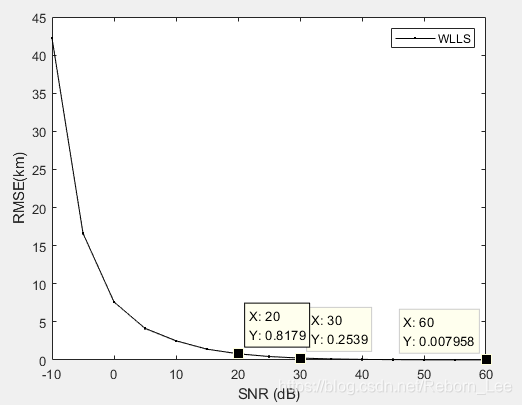
從下圖的定位誤差分析圖中可以看出,信噪比為20dB時候的定位誤差達到了817m,信噪比為30dB時候的定位誤差為253m,這與之前的非線性方法相比,定位誤差不相上下,但是與lls方法相比,定位誤差小了一些,說明WLLS演算法確實定位準確呀。
為了方便使用,可以將WLLS演算法編寫成一個函式:
function x = wlls(X,r,sigma2) % WLLS algorithm % -------------------------------- % x = wlls(X,r,sigma2); % x = 2D position estimate % X = matrix for receiver positions % r = TOA measurement vector % sigma2 = noise variance vector % L = size(X,2); % number of receivers A = [-2*X' ones(L,1)]; b = r.^2-sum(X'.^2,2); W = 1/4*diag(1./(sigma2.*r.^2)); p = pinv(A'*W*A)*A'*W*b; x= [p(1) ; p(2)];
