以往之不鑑，來者之可追！     —2018/03/04中午做了家鄉的扁粉菜後手記

窮的本質是什麼？富又意味著什麼？你知道為什麼我們的貧富差距那麼大嗎？你知道為什麼你那麼窮或者那麼富嗎？是少數富人太惡毒？還是大量窮人太不努力？…

當我們在討論社會財富分配或者社交網路等話題的時候，往往避不開的概念包括馬太效應，冪律等。大致上的意思是在說，不到20%的人佔有了超過80%的財富，只有不到20%的網路節點卻擁有了整個網路超過80%的連結數。在以往，我以可以將這種現象通俗地理解成80/20原則或者二八定律，然而這種描述畢竟不是很精確，我們期待用數學來描述這種現象，於是很早以前就誕生了很多相關的數學理論，比如冪律等。

然而，非常令人遺憾的是，現實中的世界是及其複雜的，每一個方面的每一個細節因素都會被所有其它方面的其它細節因素所影響，這在數學上是一個不可解的問題，因此，冪律的數學描述終究是對社會現實理想化的描述

更多的時候，我們要想分析一種社會化的現象，能拿到的只是一些散點資料，我們要通過這些散點資料得到一些具有統計意義的結論，比如：

• 社會財富到底真的是冪律分佈，還是正態分佈的呢？
• 現如今的學區房分配方法對大多數人公平嗎？
• …

洛倫茲曲線

感謝洛倫茲曲線，使得我們可以在一幅圖中歸納總結並看清楚這一切。那麼，什麼是洛倫茲曲線？我通過社會財富分配的例子用自己的語言先簡單描述一下。

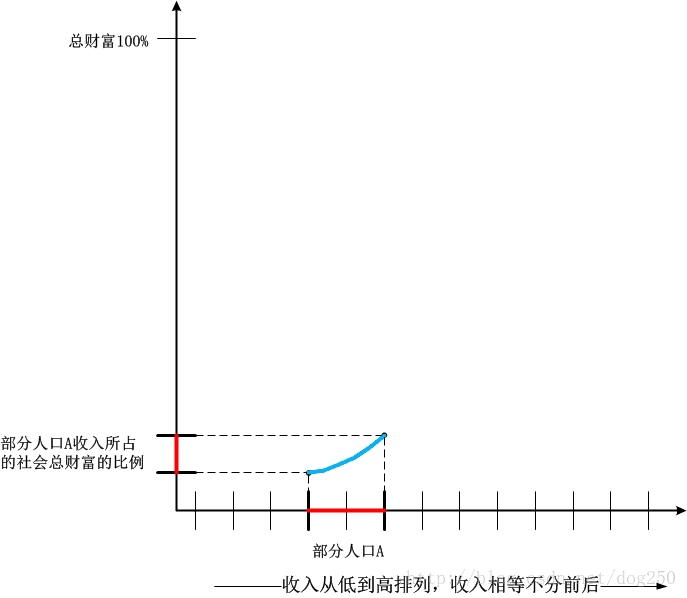
• 第一，畫出橫座標。讓參與財富分配的人按照自己收入從低到高依次從左到右等距排隊；
  
• 第二，畫出縱座標。橫座標任意區間對應的那部分人在縱座標對應區間表示他們的財富所佔總財富的比例。

• 第三，描點。把所有的散點描入基於上面兩步建立的座標系中，用平滑曲線將它們相連，這就是洛倫茲曲線。

我這裡的介紹很簡單，更詳細的描述請自行搜尋相關文獻。接下來我主要說一下洛倫茲曲線的一些性質以及我們如何從這條曲線上看出一些更為細節的東西。我的目標是希望能在一幅圖上看到更多的東西。

洛倫茲曲線的性質

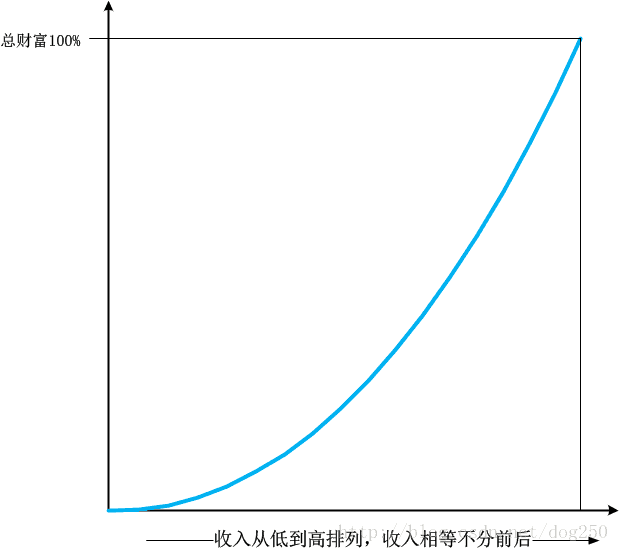
由於洛倫茲曲線的橫座標表示的人口是按照收入從低到高排隊的，那麼曲線從左到右，每增加一個人，其對積累人口財富比例的貢獻應該是逐步增加。換句話說，曲線的斜率正是該點所對應人口的收入絕對值(歸一化後的絕對值)，由於橫座標是排序的，所以我們得出一個性質：

洛倫茲曲線一定是下凸的，隨著橫座標增加，其對應點的斜率單調遞增。

  另外，橫座標上的點到原點的距離表示的是積累人口，把所有人口作為單位1並取百分比的話，橫座標的做大標度就是1，而縱座標表示財富百分比，它的最大標度自然就是1，也就是100%，因此，有第二個性質：

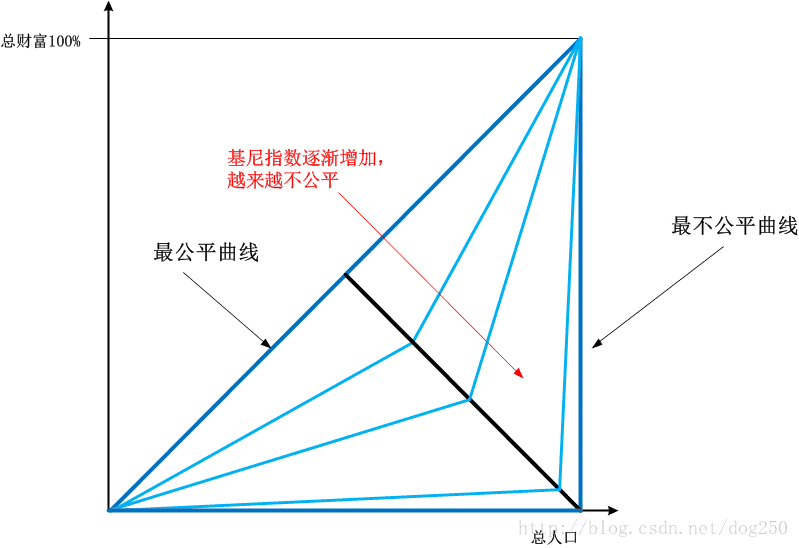
洛倫茲曲線被圍在(0,0)上的情況就好了：

看來，用面積的比值計算而得到的基尼指數，真的可以直觀地表示出不公平程度。現在的問題是，洛倫茲曲線能否提供一種動力學的解釋，讓我們看到更加深刻的造就這條曲線的內在原因呢？就是說“巨大的不公平(即馬太效應)到底是大量的窮人導致的呢，還是少量富人導致的呢？”，這就是在問：

是大量的窮人造就了少量富人呢，還是少量富人引起了大量窮人的產生？

詭異的因果輪迴

上節最後的提問，我相信大多數的回答是後者，或者情願認為是後者，然而，我覺得恰恰相反，馬太效應的根源在於大量窮人的不努力，而不是少量富人的努力，這個結論用於針對連結數計量權重的複雜網路也是適用的，比如社交圈，比如網際網路。

  我就問下面兩種平衡哪種更容易維持吧：

必然是第一個更容易維持平衡，因為不需要費勁，這是一個負反饋，而第二個平衡如果想維持，必然要持續注入能量，這是一個正反饋，一旦偏離，便萬劫不復地跌落。這非常好理解，你想窮的話，簡單放鬆任其自然就好了，如果想富，就必然不斷努力，即便你想搞點不義之財，也不能守株待兔吧…

  假設一開始財富(包括任意資源)的分配是公平的，我們來看看事情如何演化：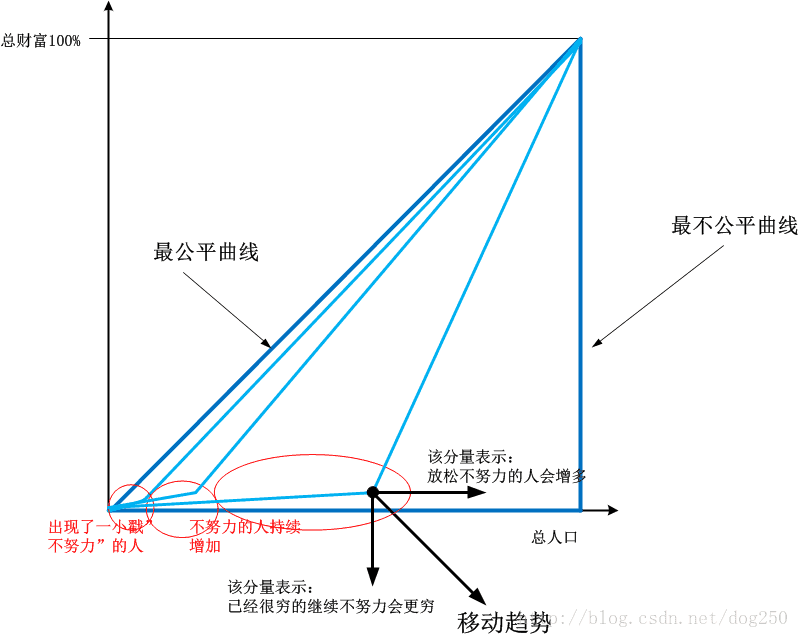

理解為什麼一開始有人會在完全公平的時候首先變窮非常容易，你只需要鬆懈一口氣，你也會變窮，而鬆懈一口氣幾乎是毫無費力的，這正是一切的趨勢，因為每一個人都希望儘可能省力！

  我們假設已經存在的財富不會消亡，不會銷燬，那麼一部分窮人鬆懈導致的他們主動放棄的財富便會被動的轉移到另一部分稍微努力一點的人手中，造成最初的不均衡。有人會問，為什麼會有努力的人，大家難道不能一起鬆懈嗎？

  這個問題很好。我這裡的假設是基於正態分佈統計的，我的假設是大部分人都維持現狀，然後少部分人鬆懈，少部分人努力一點點。但是要知道，這個正態分佈只是一個瞬間量，因為鬆懈毫不費力，致富需要努力這個原因，鬆懈的人越來越多。

  但是富人卻不會越來越多，而是已經富的人會越來越富。這是一個一將功成萬骨枯的模型，而不是集體大生產的模型。這是為什麼？因為起初致富的那一小戳人是起初鬆懈的那一小撮人造就的，然而他們卻為自己增加了一點點正能量，這個比別人多了一點的能量可以讓他們獲取窮人放棄的財富時更佔先機，顯然，這是一個遞迴滾雪球的過程，這個過程可以定性地解釋馬太效應的成因。

財富是一個低熵體，必然要注入能量而產生或者擁有，這是一個費力做功的過程。

好吧，我承認，如果我真的相信了我自己在上面扯的那一通，那麼在人類文明已經持續進化了7000年左右的今天，我將大概率是一個一無所有的人，你也一樣，財富幾乎會被個位數的人佔據，我們所有人幾乎都是奴隸…確實如此，在3000以前，確實是這樣，摩西的出埃及就是在這種背景下發生的，後來的赫梯，亞述，波斯，羅馬共和國，希臘這些都是這樣。但是現在，我們發現不再是這樣，至少對於我個人而言，雖然我也經常鬆懈而不努力，但我過得還不錯，難道我上面的論述錯了嗎？

  還是那個緣由，世界不是一種因素主導的。當初認為工業資產階級一定會被經濟危機摧毀的那些理論家忽略了一個事實，那就是工廠出產的所謂可以成為過剩產品的東西有一個巨大的消費群體，那就是工人本身，如果工廠主知道這個事實，就會給工人適當加薪，用這些薪水去買自己出品的東西…你和我之所以過的不錯，正因為此。

  網際網路外賣很風靡，但是其重要的消費群體正是網際網路行業的人，美團，餓了麼的員工自己也點外賣…我們把自己上班做出來的東西賣給了汽車廠的員工，然後我們卻買了他們生產的汽車…遍身羅綺者，不是養蠶人的時代已經過去了，在群體看來，自產自銷才是根本。

  自產自銷確實能維持社會低熵體的持續低成本轉動，裡面就好像有一個渦輪增壓系統。理想情況下，如果能形成一條咬尾蛇就更棒了，這條蛇不斷把吞掉自己的身體，不斷長胖…

  還有一個問題沒有解釋，如果那個黑色圓點達到了最右下端會怎樣？…省略幾萬字…會發生類似法國1789年的事情，其實不到那個點就發生了，然後會怎樣？然後會再度從新的完全公平線重新開始，直到永遠！新的理論來了：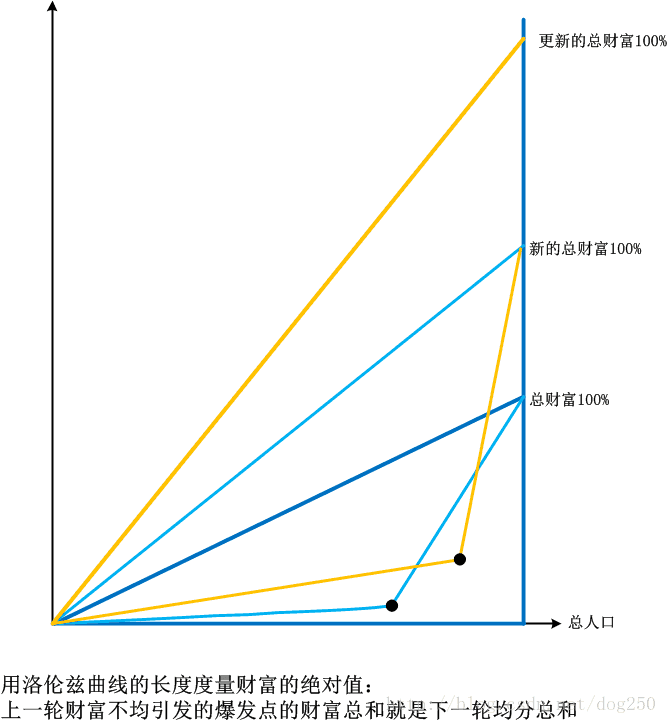

上述圖示中，相同顏色的曲線長度相同。

  人口不變的情況下，總的財富會增加，當不公平程度達到極限時，總的財富就會被主動重新分配，然後整體上就會被動重新達到新的不公平極限。我們的世界就是這麼發展下去不斷達到新的高度的。

正態分佈和馬太效應

馬太效應真的是一個普遍現象，不然它不會在兩千年前的《馬太福音》裡出現。古典著作裡描繪的幾乎都是當時的社會現狀，而不是什麼神的預言或者箴言，藉由神的口吻表達而已，以爭取信眾。這就好比那些脫口秀演員們口中的“我有一個朋友…”那般。

  文章要結束了，我還是有一個問題搞不懂，為什麼自然界包括社會上的很多現象都有馬太效應呢？正式一點說，為什麼冪律是普遍現象呢？

  其實，正態分佈也是普遍現象，我們等車的時候，我們統計身高體重的時候，在預估自己會不會得癌症的時候…但是往往這都不會引起我們的關注，反而針對冪律，我們時刻關注自己是不是處在那個長尾的部分…這很有意思。

  大體上來講，我覺得獨立事件往往遵循正態分佈，而相關事件則遵循冪律。身高就是一個獨立事件，同班同學裡具有血緣關係的情況幾乎可以忽略，每一個人都是獨立的個體，誰也不影響誰，因此班級裡的同學的身高就是正態分佈。而收入則不是這樣，你在去某家公司，或者決定追隨某人時，肯定要先看看這個公司或者個人有沒有被別人追隨過，從而選取被追隨的最多的公司或者個人，以最大限度用別人的時間來降低自己的風險，這就是為什麼大家都喜歡去大公司比如BAT上班的原因。也正因為此，在魏晉南北朝前期，五胡亂華，很多漢人都躲進了塢堡，因此也就成全了很多豪族，這些豪族正是後面隋唐時期建設國威的中流砥柱，直到宋朝其財富才被平均。

時間，空間，冪律，正態分佈

時間換空間

最大限度利用別人在時間維度上的經驗來降低自己在瞬間空間選擇上的風險，這是一個典型的模式，該模式也許就是非獨立事件形成冪律的成因，因為該模式把時間和空間耦合了。

  其實把時間和空間作為對等的維度展開，我們可以發現最終的冪律是不存在的，一切都是正態分佈。之所以有些分佈看起來是冪律，那是因為時間維度被壓縮了，實際上，換句話說，冪律只是空間維度上的說法。

  當我們說80%的財富集中在20%人手中的時候，我們隱含的意思是“當下，現在這個時候”，如果我們把時間維度也算進去，就可以發現，富人積累財富的時間要遠遠大於窮人放棄財富的時間，按照時間展開，富人的財富會被拉伸，也就是說，在總的時間段看來，並沒有窮人和富人之間的關於財富的冪律分佈。

  同樣的理論可以解釋為什麼歐洲在近代率先提出了國債而中國沒有，原因就是歐洲用時間換了空間，歐洲稅率一直都很高，因為它們的國家都很小，為了支付昂貴的列國戰爭開銷並保持自己的穩定，稅率很難進一步提高，只能在時間上做文章，即在同一時間點徵收未來幾年的稅並支付時間成本換算成貨幣後的利息，這就是國債的本質。然而在中國，龐大的領土可以在空間上展的很開，即便是鉅額的稅收，分攤到這麼大的空間內，每一部分也不會太多，這是一個典型的時間/空間不對稱壓縮的例子。事實上，普遍存在的借錢給利息，期貨之類的，都包含了類似的意思。

下面一篇文章，我將用我上面的這個模型來解釋一下為什麼世界的精彩來自精英的創造這件事。
…
  
去年元夜時，花市燈如晝。
月上柳梢頭，人約黃昏後。
今年元夜時，月與燈依舊。
不見去年人，淚溼春衫袖。