float型別在記憶體中佔4位元組，最高位表示符號位，剩下31位，從右向左取8位用於表示指數，其餘用於表示尾數

在進行二進位制轉化前，需要進行科學記數法轉換，具體步驟如下

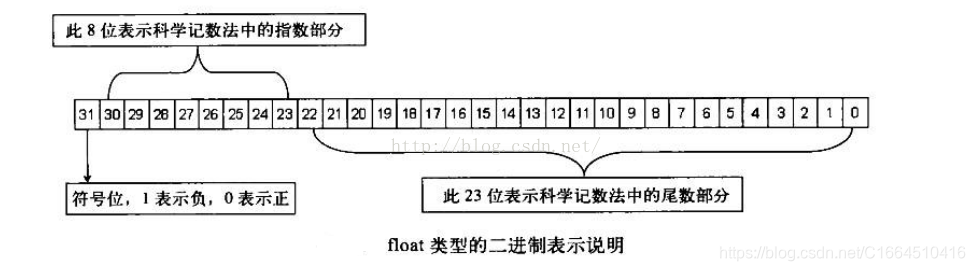
1.看符號位，正數為0，負數為1

2.將數轉化為相應的二進位制數

3.用科學記數法轉化為相應的形式 如：1.xxxxxx*2^n()

4.n為指數，加上127

5..轉化後用二進位制拼接寫出

舉個例子

12.25用IEEE編碼的顯示

1.是正數，符號位為0

2.12.25的二進位制數為1100.01

3.用科學記數法表示為  1.10001*2^3(整數部分為1100，小數部分為01，小數點向左移動，每移動一次加一，遇1停止 即為n的演算法)

可得  指數n為3，尾數部分為10001

4.指數n加上127         3+127=130轉化為二進位制為10000010

5.尾數位為10001000000000000000000（當不足23位時，低位補0填充）

拼接後為0 10000010 10001000000000000000000

當數為負數也是同樣的道理

注：1.  為什麼要加127呢，十進位制127用二進位制表示數01111111，IEEE碼規定指數域小於01111111為負數，大於為正數，所以01111111為0

還有可能出現無窮的情況，小數部分是個無窮值，比如1.3f，小數部分轉化為二進位制為無窮的，尾數部分無法儲存完，只儲存23位的，由於在轉化為二進位制的時候捨棄了部分的值，所以取得值為近似值，這就解釋了浮點數值是否為0時，要做一個區間比較而非等值比較，具體程式碼如下：

float fTemp =0.0001f

if(fFloat >= -fTemp && fFloat <=fTemp)

{

     //fTemp=0

}