陣列11——稀疏矩陣的壓縮儲存1——基本內容
【定義】
所謂稀疏矩陣,假設在m×n矩陣中,有t個元素不為零,令δ=t/(m×n),δ為矩陣的稀疏因子,如果δ≤0.05,則稱矩陣為稀疏矩陣。通俗的來講,若矩陣中大多數元素的值為零,只有很少的非零元素,這樣的矩陣就是稀疏矩陣。
如圖就是一個稀疏矩陣
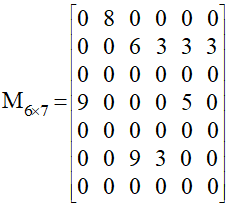
【三元組表示】
為了節省記憶體單元,需要對稀疏矩陣進行壓縮儲存。在進行壓縮儲存的過程中,我們可以只儲存稀疏矩陣的非零元素,為了表示非零元素在矩陣中的位置,還需儲存非零元素的行號和列號(i,j)。這樣通過儲存非零元素的行號、列號和元素值即可將稀疏矩陣壓縮儲存,我們把這種儲存方式稱為稀疏矩陣的三元組表示。
三元組的結點結構如圖所示。

上面的稀疏矩陣用三元組表示如下:
((0,3,5),(1,1,8),(2,2,6),(2,3,3),(2,3,3),(3,0,9),(3,4,5),(4,2,9),(4,3,3),(5,4,1))
若將這些三元組按照行序為主序存放在一維陣列中,如圖所示,我們將這種採用順序儲存結構的三元組稱為三元組順序表,其中k表示一維陣列的下標。
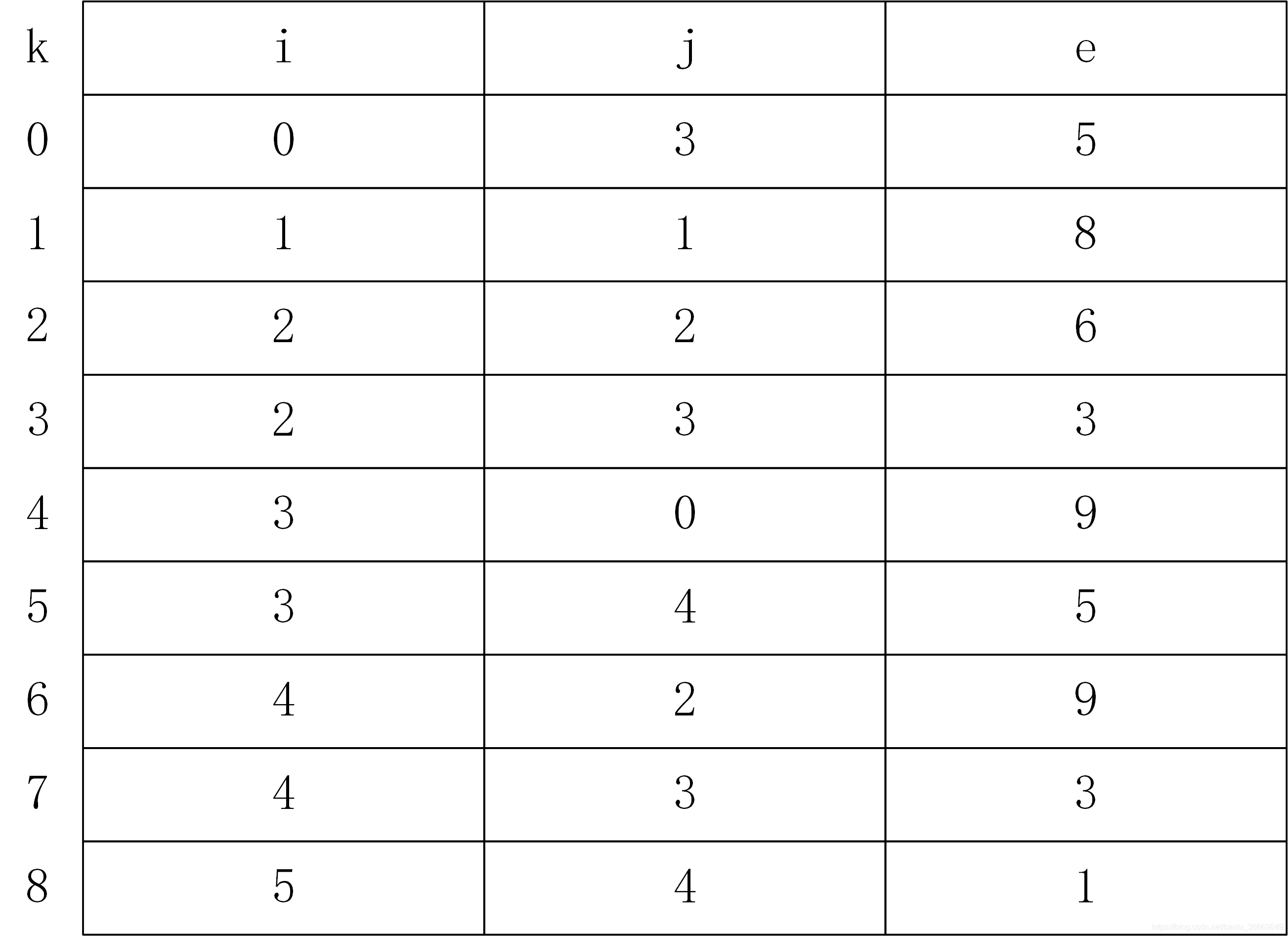
三元組順序表的型別用C語言描述如下:
#define MAXSIZE 100
typedef struct
{
int i;
int j;
DataType e;
}Triple;
typedef struct
{
Triple data[MAXSIZE];
int m;
int n;
int len;
}TriSeqMatrix;
【稀疏矩陣的轉置】
稀疏矩陣(三元組表示)的基本運算包含建立三元素矩陣、三元組的銷燬矩陣、三元組的複製、輸出等基本運算(TriSeqMatrix.h)。
稀疏矩陣的轉置。稀疏矩陣的轉置就是要將矩陣中元素由原來的存放位置(i,j)變成(j,i),也就是說將元素的行列互換。例如下圖就是一個6×7矩陣經過轉置後變為7×6的矩陣,並且矩陣的元素也要以主對角線為基準進行變換。
將稀疏矩陣轉置的方法:
將三元組中的元素進行行列互換即可得到轉置後的矩陣。(i,j,e)→(j,i,e)
下圖展示了一個矩陣進行轉置的過程:
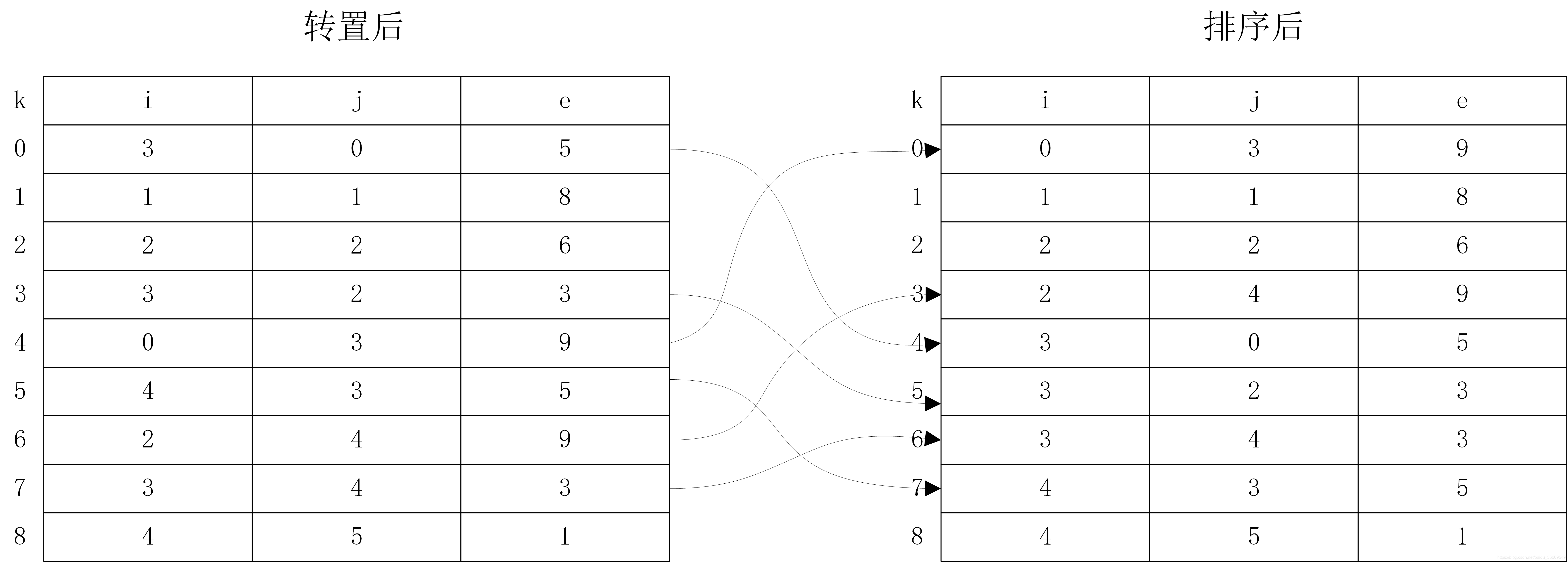
行列下標互換後,為了保證轉置後的矩陣仍然按照行序優先排列,還需要將行、列下標重新排序。另外,還有一種方法可以減少這種排序,那就是以列優先順序進行轉置,轉置後的三元組順序表剛好是以行序優先存放的。
演算法思想:
掃面三元組順序表M,找到j=0的元素,將行號和列號互換後存入到三元組N中。再第二趟掃面M,找到j=1的元素,將行號和列號互換存入到三元組順序表N中。依此類推,直到所有元素都存放在N中。
如圖所示
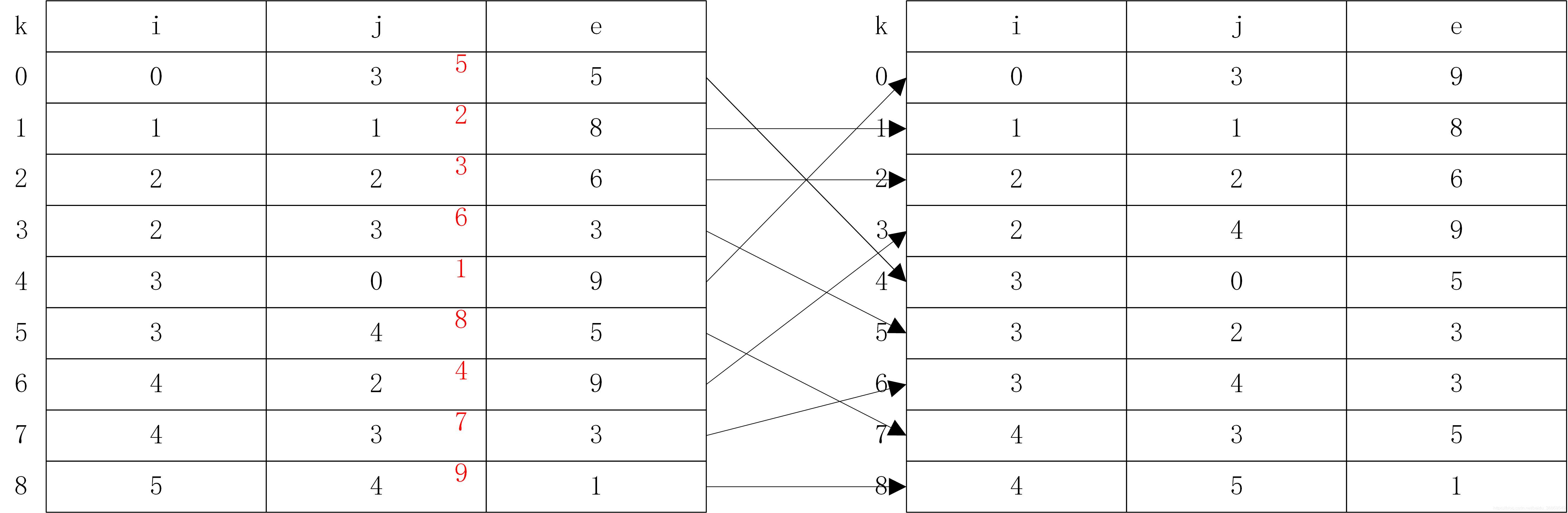
稀疏矩陣轉置的演算法實現如下:
void TransposeMatrix(TriSeqMatrix M,TriSeqMatrix *N)
/*稀疏矩陣的轉置*/
{
int i,k,col;
N->m=M.n;
N->n=M.m;
N->len=M.len;
if(N->len)
{
k=0;
for(col=0;col<M.n;col++) /*按照列號掃描三元組順序表*/
for(i=0;i<M.len;i++)
if(M.data[i].j==col) /*如果元素的列號是當前列,則進行轉置*/
{
N->data[k].i=M.data[i].j;
N->data[k].j=M.data[i].i;
N->data[k].e=M.data[i].e;
k++;
}
}
}
通過分析該轉置演算法,其時間複雜度主要是在for迴圈語句上,因此演算法的時間複雜度為O(n*len)。當非零元素的個數len與m*n同數量級時,演算法的時間複雜度就變為O(m*n*n)。如果稀疏矩陣仍然採用二維陣列存放,則轉置演算法為:
for(col=0;col<M.n;++col)
for(row=0;row<M.len;row++)
N[col][row]=M[row][col];
上述演算法的時間複雜度為O(n*m升}4、}此可以看出,採用三元組順序表示雖然節省了儲存空問,但時間複雜度卻增加了。在演算法設計過程中時間複雜度和空間複雜度就是一個此消彼長的過程,降低了時間複雜度,就勢必以犧牲空間複雜度為代價,反之亦然,演算法設計就是時間複雜度和空間複雜度的一種折中考慮為了降低時間複雜度,可以考慮用稀疏矩陣的快速轉置演算法。
