【動態規劃】最小編輯距離(字串A到字串B變化最少要多少步)
最小編輯距離是一道非常經典的動態規劃問題。
設A 和B 是2 個字串。要用最少的字元操作將字串A 轉換為字串B。
這裡所說的字元操作包括
(1)刪除一個字元;
(2)插入一個字元;
(3)將一個字元改為另一個字元。
將字串A變換為字串B 所用的最少字元操作次數也稱為字串A到B 的編輯距離,記為 d(A,B)。
試設計一個有效演算法,對任給的2 個字串A和B,計算出它們的編輯距離d(A,B)。
為什麼要把這個問題又搬出來呢?因為我發現,網路上有好多錯誤程式碼,錯誤思路,這種錯誤程式碼,流傳甚廣,被多個部落格學習又再次推廣發表。我覺得應該糾正一下了。
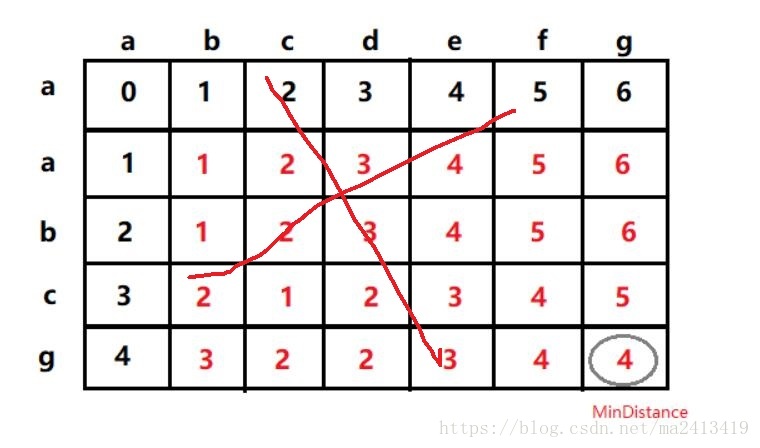
先說一下錯誤的版本。以下位置座標皆從0開始計數。
凡是用到這張圖的,全是錯誤的!
為什麼這麼說呢?我講下每一個單元格的數字代表的意義。如上圖所示,比如(0,6)位置的數字6 代表字串“abcdrfg”變為字串“a”需要的最少步數為6,再比如(1,1,)位置處的數字1代表字串“ab”變為字串“aa”需要的最少步數為1。
乍一看,這張圖也沒問題啊,然而這種寫法是錯誤的,這張圖成立只基於兩個字串的首字母相同的情況。配有這張圖的大部分部落格中的程式碼都是錯誤的。比如“a”和“b”,也會檢測為需要0步。
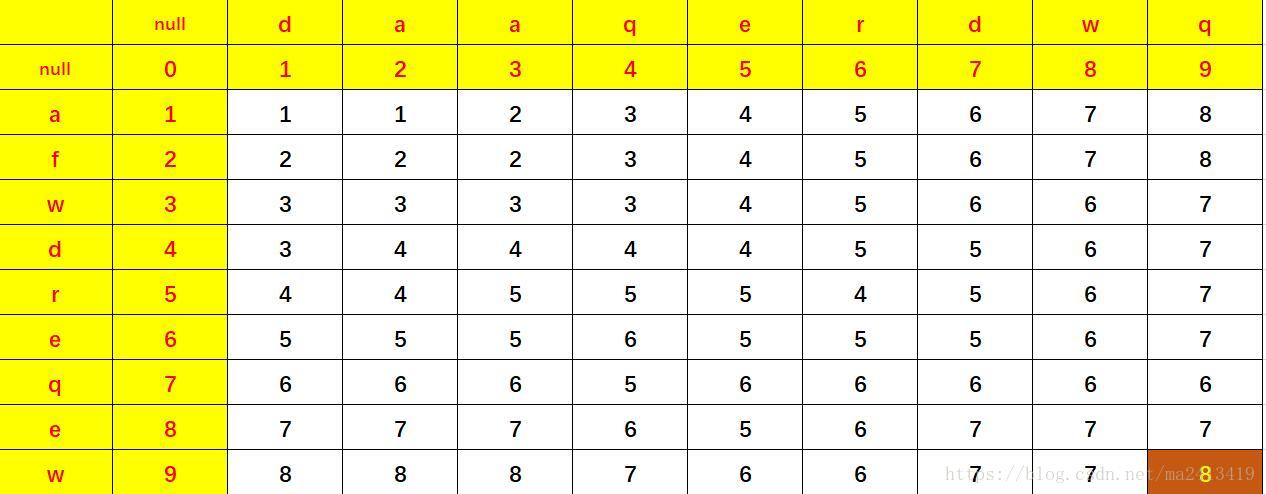
真正的圖為:
該圖中示例為字串“daaqerdwq”轉化為字串“aswdreqew”。
此時我們可以看到位於(2,2)位置的數字1,對應的是字串“d
這個思路是怎麼來的呢?首先假設兩個字串都為空,則需要0步就可轉化。所以表格最左上角要寫0,然後字串A加入一個字元‘d’,此時需要1步才能做到轉化,同理,若是B為空字串,A字串有幾個字元,就要做幾步刪除操作。
若是字串B中有一個字元,如上圖中的“a”,重複A字串從“ ”到“daaqerdwq”不斷加入字元的過程,即可得出如下規律
D[i][j]=min(min(D[i-1][j]+1,D[i][j-1]+1),(A[j-1]==B[i-1]?D[i-1][j-1]:D[i-1][j-1]+1));
D[i][j]是指上圖中數字區域的每個單元格的值。
完整程式碼如下:
#include<iostream>
#include<string>
using namespace std;
int MinEditDistance(string A,string B)
{
int len_A = A.length();
int len_B = B.length();
int D[len_B+1][len_A+1];
D[0][0]=0;
for(int i=1;i<=len_A;i++)
{
D[0][i]=i;
}
for(int i=1;i<=len_B;i++)
{
D[i][0]=i;
}
for(int i=1;i<=len_B;i++)
{
for(int j=1;j<=len_A;j++)
D[i][j]=min(min(D[i-1][j]+1,D[i][j-1]+1),(A[j-1]==B[i-1]?D[i-1][j-1]:D[i-1][j-1]+1));
}
return D[len_B][len_A];
}
int main()
{
string A,B;
cin>>A>>B;
cout<<MinEditDistance(A,B);
}
雖說天下部落格一般抄,但大家還是不要去借鑑錯誤的部落格了。