哈夫曼樹的建立和操作
阿新 • • 發佈:2018-12-22
哈夫曼樹的引進是與帶有權重的二叉樹有關的
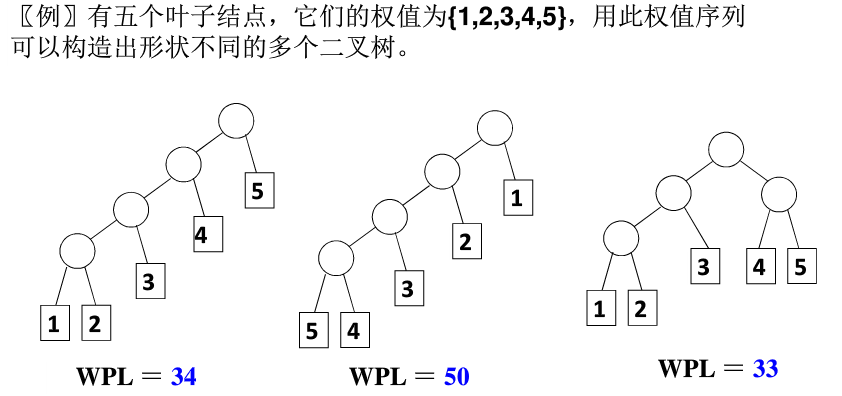
首先定義帶權路徑長度(WPL):設二叉樹有n個葉子結點,每個葉子結點帶有權值
最優二叉樹或哈夫曼樹:WPL最小的二叉樹
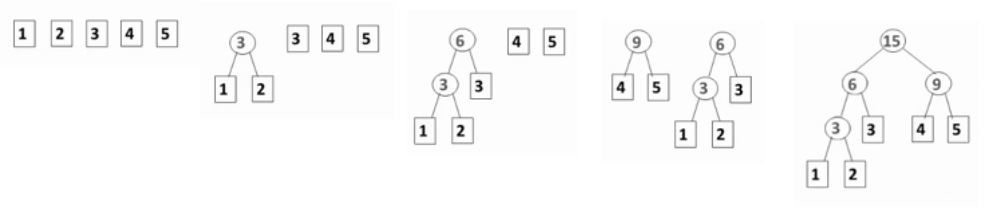
那麼如何建立一棵哈夫曼樹呢,哈夫曼提出了一種方法,就是每次把權值最小的兩棵二叉樹合併,例如下圖所示
這就可以用到堆,每次把新生成的樹插入進堆,然後彈出兩個樹依次就是最小的樹,揭下來就是具體的實現了,首先是把之前的最小堆改為最大堆,然後把Elements的型別改掉,最後是寫Huffman樹
#include <stdio.h> 重點有這麼兩個地方
MinHeap Create(int MinSize){
MinHeap H=(MinHeap)malloc(sizeof(struct HeapStruct));
H->Elements=(ElementType *)malloc((MinSize+1)*sizeof(ElementType));//從小標為1的地方開始存放
//for(int i=0;i<=MinSize;i++)
//H->Elements[i]=(HuffmanTree)malloc(sizeof(TreeNode));
for(int i=0;i<=MinSize;i++)
{
H->Elements[i]=(ElementType )malloc(sizeof(ElementType));//從小標為1的地方開始存放
H->Elements[i]->Weight=0;//定義“哨兵”為大於堆中所有可能元素的值,便於以後更快操作
H->Elements[i]->Left=NULL;
H->Elements[i]->Right=NULL;
}
H->Size=0;
H->Capacity=MinSize;
H->Elements[0]->Weight=MinData;//定義“哨兵”為大於堆中所有可能元素的值,便於以後更快操作
return H;
//時間複雜性是O(logN)
}; 一個是這裡建立時的malloc竟然有三次。。還是請同學幫我解決的
另外一個是下面Huffman樹的生成函式
HuffmanTree Huffman(MinHeap H){
//假設H->Size個權值已經存在H->Elements[]->Weight裡
int i;HuffmanTree T;
BuildHeap(H);//將堆調整為最小堆
int len=H->Size;
for(i=1;i<len;i++){//做H->Size-1次合併
T=(HuffmanTree)malloc(sizeof(struct TreeNode));//建立新結點
T->Left=DeleteMin(H);
T->Right=DeleteMin(H);
T->Weight=T->Left->Weight+T->Right->Weight;
Insert(H,T);
}
T=DeleteMin(H);
return T;
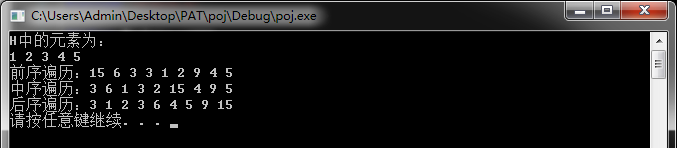
};下面是實現效果
最後附上一段小程式碼
//整數轉化為樹之後再插入
void Insertint(MinHeap &H,int item){
int i;
if(IsFull(H)){
printf("最小堆已滿\n");
return;
}
i=++H->Size;//先Size自加1再賦給i,i指向插入後堆中的最後一個元素
ElementType E1=(ElementType )malloc(sizeof(ElementType));
E1->Right=E1->Left=NULL;
E1->Weight=item;
for(;H->Elements[i/2]->Weight>E1->Weight;i/=2)
H->Elements[i]=H->Elements[i/2];//向下過濾結點
//哨兵的作用就是避免插入的值比Elements[0]還小
H->Elements[i]=E1;//將item插入,執行速度比交換快
//時間複雜性是O(logN)
}; 這樣就可以呼叫
MinHeap H= Create(15);
Insertint(H,55);
Insertint(H,79);
Insertint(H,66);
Insertint(H,83);
Insertint(H,72);
Insertint(H,30);
Insertint(H,49);
Insertint(H,91);
Insertint(H,87);
Insertint(H,43);
Insertint(H,9);
Insertint(H,38);
Print(H);
DeleteMin(H);
DeleteMin(H);
Print(H); 等語句,哦耶終於完成啦^^