哈夫曼樹及哈夫曼編碼和解碼
阿新 • • 發佈:2018-11-10
哈夫曼樹,又稱最優樹,是帶權路徑最小的樹。
基本概念:
節點間的路徑長度:兩個節點間所包含的邊的數目。
樹的路徑長度:從根到樹中任意節點的路徑長度之和。
權:將節點賦予一定的量值,該量值成為權。
樹的帶權路徑長度:樹中所有葉子結點的帶權路徑長度。
哈夫曼演算法:給定一個儲存權值的陣列,求最優樹的演算法。對於此權值陣列找出其中最小的權值和第二小的權值,用這兩個權值建立樹,並把這兩個權值相加所得作為一個新權值放入到原陣列中(注意:此時陣列中已經去掉了剛才用過的權值),重複以上操作即可建立最優樹。
哈弗曼編碼和解碼的優點不再贅述。
哈夫曼樹的實現
1.建立結構體,比較簡單
typedef 2.利用權值陣列建立哈夫曼樹(程式碼註釋已相對清晰)
Tree *create(int *a,int n){//對陣列 a 進行實現哈夫曼樹 a 中存放的為權值, n 為陣列的長度
Tree *tree;
Tree **b;
int i,j;
b = malloc(sizeof(Tree)*n);//動態一維陣列的申請來儲存權值
for(i = 0; i < n; i++){
b[i] = malloc(sizeof(Tree) 3.列印哈夫曼樹
//列印哈夫曼樹
void print(Tree *tree){
if(tree){
printf("%d ",tree->data);
if(tree->left && tree->right){
printf("(");
print(tree->left);
if(tree->right)
printf(",");
print(tree->right);
printf(")");
}
}
}
4.獲取哈夫曼樹的帶權路徑長度
//獲得哈夫曼樹的帶權路徑長度
int getWeight(Tree *tree,int len){
if(!tree)
return 0;
if(!tree->left && !tree->right)//訪問到葉子結點
return tree->data * len;
return getWeight(tree->left, len + 1) + getWeight(tree->right,len + 1);//訪問到非葉子結點
}
5.下面便是哈夫曼編碼與解碼,思路也較為簡單
//哈夫曼編碼
void getCoding(Tree *tree,int len){
if(!tree)
return;
static int a[20]; //定義靜態陣列a,儲存每個葉子的編碼,陣列長度至少是樹深度減一
int i;
if(!tree->left && !tree->right){
printf(" %d 的哈夫曼編碼為:",tree->data);
for(i = 0; i < len; i++)
printf("%d",a[i]);
printf("\n");
}
else{//訪問到非葉子結點時分別向左右子樹遞迴呼叫,並把分支上的0、1編碼儲存到陣列a ,的對應元素中,向下深入一層時len值增1
a[len] = 0;
getCoding(tree->left, len + 1);
a[len] = 1;
getCoding(tree->right, len + 1);
}
}
6.哈夫曼解碼,比較容易實現
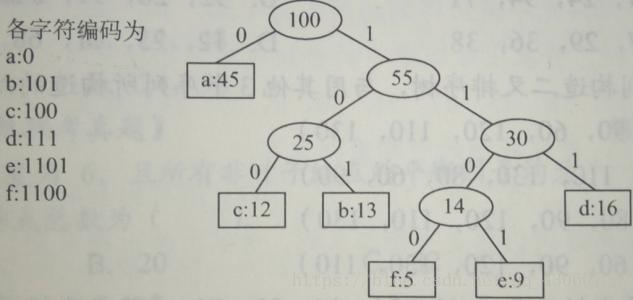
節點與左子節點之間記為 0 ,節點與右節點之間記為 1 ,如圖
//哈夫曼解碼
void Decoding(Tree *tree){
printf("請輸入要解碼的字串\n");
char ch[100];//輸入的待解碼的字串
gets(ch);
int i;
int num[100];//用於儲存字串對應的0 1 編碼對應的節點
Tree *cur;
for(i = 0; i < strlen(ch); i++){
if(ch[i] == '0')
num[i] = 0;
else
num[i] = 1;
}
if(tree){
i = 0;
while(i < strlen(ch)){
cur = tree;
while(cur->left && cur->right){
if(num[i] == 0)
cur = cur->left;
else
cur = cur->right;
i++;
}
printf("%d",cur->data);
}
}
}
完整程式碼如下
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Tree{
struct Tree *left;
struct Tree *right;
int data;
}Tree;
Tree *create(int *a,int n){//對陣列 a 進行實現哈夫曼樹 a 中存放的為權值, n 為陣列的長度
Tree *tree;
Tree **b;
int i,j;
b = malloc(sizeof(Tree)*n);//動態一維陣列的申請來儲存權值
for(i = 0; i < n; i++){
b[i] = malloc(sizeof(Tree));
b[i]->data = a[i];
b[i]->left = b[i]->right = NULL;
}
//建立哈夫曼樹
for(i = 1; i < n; i++){
int small1 = -1,small2;//small1指向權值最小,small2是第二小,其初始指向分別是陣列的前兩個元素
//注意前兩個元素並不一定是最小的和第二小的
//下面一個 for 迴圈是讓small1指向第一個權值,small2指向第二個權值
for(j = 0; j < n; j++){
if(b[j] != NULL && small1 == -1){
small1 = j;
continue;
}
if(b[j] != NULL){
small2 = j;
break;
}
}
//接下來就是對陣列剩下的權值逐個與small1、small2比較,找出最小與第二小的權值
for(j = small2; j < n; j++){
if(b[j] != NULL){
if(b[j]->data < b[small1]->data){
small2 = small1;
small1 = j;
}
else if(b[small2]->data > b[j]->data){
small2 = j;
}
}
}
//由兩個最小權值建立新樹,tree 指向根節點
tree = malloc(sizeof(Tree));
tree->data = b[small1]->data + b[small2]->data;
tree->left = b[small1];
tree->right = b[small2];
//以下兩步是用於重複執行
b[small1] = tree;
b[small2] = NULL;
}
free(b);
return tree;
}
//列印哈夫曼樹
void print(Tree *tree){
if(tree){
printf("%d ",tree->data);
if(tree->left && tree->right){
printf("(");
print(tree->left);
if(tree->right)
printf(",");
print(tree->right);
printf(")");
}
}
}
//獲得哈夫曼樹的帶權路徑長度
int getWeight(Tree *tree,int len){
if(!tree)
return 0;
if(!tree->left && !tree->right)//訪問到葉子結點
return tree->data * len;
return getWeight(tree->left, len + 1) + getWeight(tree->right,len + 1);//訪問到非葉子結點
}
//哈夫曼編碼
void getCoding(Tree *tree,int len){
if(!tree)
return;
static int a[20]; //定義靜態陣列a,儲存每個葉子的編碼,陣列長度至少是樹深度減一
int i;
if(!tree->left && !tree->right){
printf(" %d 的哈夫曼編碼為:",tree->data);
for(i = 0; i < len; i++)
printf("%d",a[i]);
printf("\n");
}
else{//訪問到非葉子結點時分別向左右子樹遞迴呼叫,並把分支上的0、1編碼儲存到陣列a ,的對應元素中,向下深入一層時len值增1
a[len] = 0;
getCoding(tree->left, len + 1);
a[len] = 1;
getCoding(tree->right, len + 1);
}
}
//哈夫曼解碼
void Decoding(Tree *tree){
printf("請輸入要解碼的字串\n");
char ch[100];//輸入的待解碼的字串
gets(ch);
int i;
int num[100];//用於儲存字串對應的0 1 編碼對應的節點
Tree *cur;
for(i = 0; i < strlen(ch); i++){
if(ch[i] == '0')
num[i] = 0;
else
num[i] = 1;
}
if(tree){
i = 0;
while(i < strlen(ch)){
cur = tree;
while(cur->left && cur->right){
if(num[i] == 0)
cur = cur->left;
else
cur = cur->right;
i++;
}
printf("%d",cur->data);
}
}
}
int main(int argc, char *argv[]) {
int a[4] = {2,6,7,3};
Tree *tree = create(a,4);
print(tree);
printf("\n哈夫曼樹的權值為:");
printf("%d\n",getWeight(tree,0));
getCoding(tree,0);
printf("解碼時請參照上方編碼\n");
Decoding(tree);
}
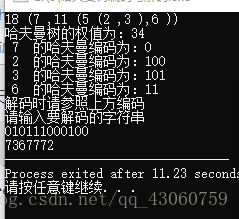
執行結果如下