題目描述

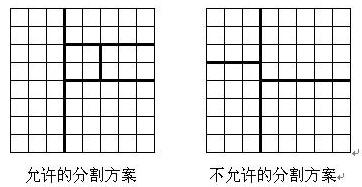
將一個８*８的棋盤進行如下分割：將原棋盤割下一塊矩形棋盤並使剩下部分也是矩形，再將剩下的部分繼續如此分割，這樣割了n-1次後，連同最後剩下的矩形棋盤共有n塊矩形棋盤。（每次切割都只能沿著棋盤格子的邊進行）

原棋盤上每一格有一個分值，一塊矩形棋盤的總分為其所含各格分值之和。現在需要把棋盤按上述規則分割成n塊矩形棋盤，並使各矩形棋盤總分的均方差最小。
均方差σ=∑ni=1(xi−x¯)2n−−−−−−−−√，其中平均值x¯=∑ni=1xin，xi為第i塊矩形棋盤的總分。
請程式設計對給出的棋盤及n，求出σ的最小值。

輸入

第1行為一個整數n

(1<n<15)。
第2行至第9行每行為8個小於100的非負整數，表示棋盤上相應格子的分值。每行相鄰兩數之間用一個空格分隔。

輸出

僅一個數，為σ（四捨五入精確到小數點後三位）。

樣例輸入

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

樣例輸出

1.633

這道題乍一看資料範圍就是DP。【暴力搜尋確實超一點】
別的人的題解已經介紹的比較全了，這裡說一下那個均方差公式的變形，否則是不能用別的題解所給的狀態轉移方程的。

#include <iostream>
 

#include <cstdio>
#include <cmath>
using namespace std;
const int INF=1<<30;
int n, chess[9][9]={0}, sum[9][9]={0}, dp[9][9][9][9][15]={0};
//直接計算矩形(y1, x1)(y2, x2)矩形分數平方
int getX(int y1, int x1, int y2, int x2){
    int a=sum[y2][x2]-sum[y2][x1-1]-sum[y1-1][x2]+sum[y1-1][x1-1];
    return a*a;
}
int main(){
    scanf("%d", &n);
    //統一i表示y，j表示x
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
            scanf("%d", &chess[i][j]);
    //計算sum陣列（矩形(1, 1)(i, j)的分數和），方便直接計算getX
    for(int i=1;i<=8;i++){
        for(int j=1;j<=8;j++)
            sum[i][j]=sum[i][j-1]+chess[i][j];
        for(int j=1;j<=8;j++)
            sum[i][j]+=sum[i-1][j];
    }
    //初值
    for(int i1=1;i1<=8;i1++)
        for(int j1=1;j1<=8;j1++)
            for(int i2=i1;i2<=8;i2++)
                for(int j2=j1;j2<=8;j2++)
                    dp[i1][j1][i2][j2][0]=getX(i1, j1, i2, j2);
    //這裡的i是切割數（分析裡的k）
    for(int i=1;i<n;i++)
        for(int i1=1;i1<=8;i1++)
            for(int j1=1;j1<=8;j1++)
                for(int i2=i1;i2<=8;i2++)
                    for(int j2=j1;j2<=8;j2++){
                        //賦值INF，若狀態不合法不會干擾其他狀態
                        dp[i1][j1][i2][j2][i]=INF;
                        //左右切割
                        for(int k=j1;k<j2;k++)
                            dp[i1][j1][i2][j2][i]=min(dp[i1][j1][i2][j2][i], min(dp[i1][j1][i2][k][i-1]+dp[i1][k+1][i2][j2][0], dp[i1][j1][i2][k][0]+dp[i1][k+1][i2][j2][i-1]));
                        //上下切割
                        for(int k=i1;k<i2;k++)
                            dp[i1][j1][i2][j2][i]=min(dp[i1][j1][i2][j2][i], min(dp[i1][j1][k][j2][i-1]+dp[k+1][j1][i2][j2][0], dp[i1][j1][k][j2][0]+dp[k+1][j1][i2][j2][i-1]));
                    }
    //套公式
    printf("%.3f\n", sqrt(double(dp[1][1][8][8][n-1])/n-double(sum[8][8]*sum[8][8])/n/n));
    return 0;
}

複雜度真嚇人。記憶化搜尋亦可。