本文將介紹並查集的模板以及各類問題中的應用

並查集，在一些有N個元素的集合應用問題中，我們通常是在開始時讓每個元素構成一個單元素的集合，然後按一定順序將屬於同一組的元素所在的集合合併，其間要反覆查詢一個元素在哪個集合中。這一類問題近幾年來反覆出現在資訊學的國際國內賽題中，其特點是看似並不複雜，但資料量極大，若用正常的資料結構來描述的話，往往在空間上過大，計算機無法承受;即使在空間上勉強通過，執行的時間複雜度也極高，根本就不可能在比賽規定的執行時間(1~3秒)內計算出試題需要的結果，只能用並查集來描述。

並查集可以算是很基礎的結構了，可以快速查詢一個元素在哪個集合中，演算法模板大致為三大塊：
1.Set(初始化)
2.Find(找到元素的祖先

1.Set
建立新集合，各集合初始時不相交。如果用fa[]陣列記錄某個元素的父親，即\(f_i=j\) i的父親為j，那麼初始化時每個元素的父親指向自己，也就是說有\(n\)個集合

    void Set(int n)
    {
        for(int i=1; i<=n; ++i)
            fa[i]=i;
        return ;
    }

2.Find

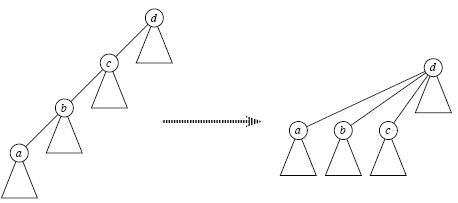
查詢元素\(x\)的根節點，也就是不斷向上找爸爸，直到尋找到某個元素\(root\)的父親指向自己時，\(root\)

所謂路徑壓縮，就是在Find的查詢路徑上把每個節點都直接指向根節點，這樣下次再找根節點的時間複雜度會變成O(1)：

    int Find(int x)
    {
        if(fa[x] == x) return x;
        return fa[x]=(Find(fa[x])); //不斷更新元素x的爸爸，同時向上尋找祖宗
    }

3.Union

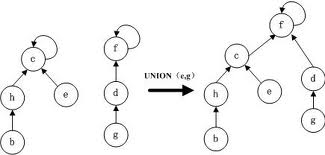
把兩個集合合併在一起，我們可以將一個集合的祖宗的父親指向另外一個集合的祖宗，此時集合數減一

    void Merge(int x, int y)
    {
        int root1=Find(x), root2=Find(y);
        if(root1 == root2) return ; //如果是一個集合就不用合併
        fa[root1]=root2; return ;
    }

$ $

那麼並查集的模板就差不多長這樣：

namespace Union_Find
{
    void Set(int n)
    {
        for(int i=1; i<=n; ++i)
            fa[i]=i;
        return ;
    }
    int Find(int x)
    {
        if(fa[x] == x) return x;
        return fa[x]=(Find(fa[x]));
    }
    void Merge(int x, int y)
    {
        int root1=Find(x), root2=Find(y);
        if(root1 == root2) return ;
        fa[root1]=root2; return ;
    }
}

using namespace Union_Find;

模板例題：
並查集模板
親戚