機器學習---演算法---邏輯迴歸
轉自:https://blog.csdn.net/ustbbsy/article/details/80423294
1 引言
最近做一個專案,準備用邏輯迴歸來把資料壓縮到[-1,1],但最後的預測卻是和標籤類似(或者一樣)的預測。也就是說它的predict的結果不是連續的,而是類別,1,2,3,...k。對於predict_proba,這是預測的概率,但概率有很多個,數目為訓練集類別(label)的個數。邏輯迴歸的原理,就是取出最大概率對應的類別。
所以邏輯迴歸,不是迴歸,而是分類器,二分類,多分類。
邏輯迴歸,是一個很有誤導性的概念。
這是個人最近的體會,入門的讀者請忽略。
2 線性迴歸
先說一下,一般模型的訓練和預測過程:
1,訓練:通過訓練資料來訓練模型,也就是通常我們所說的學習過程,即確定模型的引數。
2, 預測:訓練過後,模型引數確定,有預測資料輸入,就會得到一個結果。
常見的線性迴歸y=wx+b,我們通過訓練集來訓練出我們的模型,也就是得到我們的模型引數w,b,這樣,我們的直線或者超平面(x是多維的)就確定了。接著,對於測試集,來了一個數據x,w,b已經學習出來了,帶入y=wx+b,就會得到一個y值,也就是我們的預測值。注意, 它是浮點數。
這裡得到的y為什麼叫回歸呢,因為y不是類別(label)中的一個,它是預測出來的實數(大部分是小數)。
有的同學可能不理解什麼是迴歸?我解釋一下:
首先,需要明白二分類,類別/標籤/label是二值,{0,1}或{-1,1},總之它的類別數兩個。相信你已經知道多分類了,就是類別是多值的,{0,1,2,3,4}等,這是5類。那麼迴歸是什麼你呢。迴歸的取值,就不是像分類這樣取整數了,它是小數,浮點數,是連續的,例如(0,1)之間的取值等。
3 邏輯迴歸
前面已經說了,雖然它不是迴歸,但是名字已經確定了,大家還是這麼叫的。
前面的線性迴歸,我們已經得到y=wx+b。它是實數,y的取值範圍可以是(負無窮,正無窮)。現在,我們不想讓它的值這麼大,所以我們就想把這個值給壓縮一下,壓縮到[0,1]。什麼函式可以幹這個事呢?研究人員發現signomid函式就有這個功能。所以,他們就嘗試著,用signomid函式搞一搞這個y。
sigmoid的函式如下:
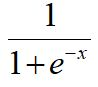
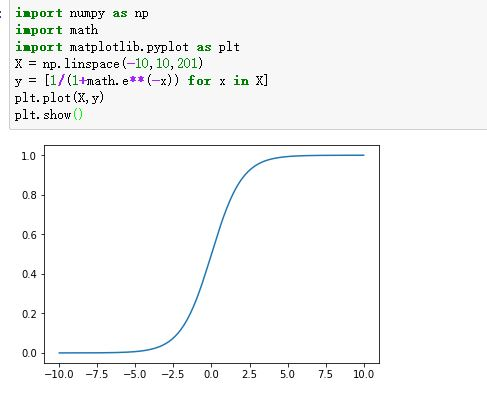
sigmoid的影象如下:
壓縮,就是把y=wx+b帶入sigmoid(x)。把這個函式的輸出,還定義為y,即:
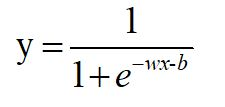
這樣,y就是(0,1)的取值。
把這個式子變換一下:
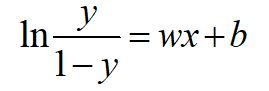
4 損失函式
損失函式,通俗講,就是衡量真實值和預測值之間差距的函式。所以,我們希望這個函式越小越好。在這裡,最小損失是0。
以二分類(0,1)為例:
當真值為1,模型的預測輸出為1時,損失最好為0,預測為0是,損失儘量大。
同樣的,當真值為0,模型的預測輸出為0時,損失最好為0,預測為1是,損失儘量大。
所以,我們儘量使損失函式儘量小,越小說明預測的越準確。
這個損失函式為:
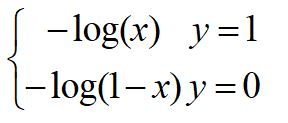
我們看看這個函式的影象:
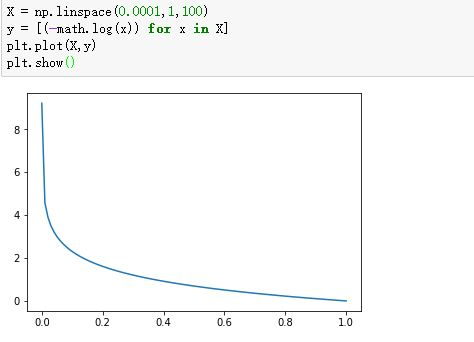
-log(x):
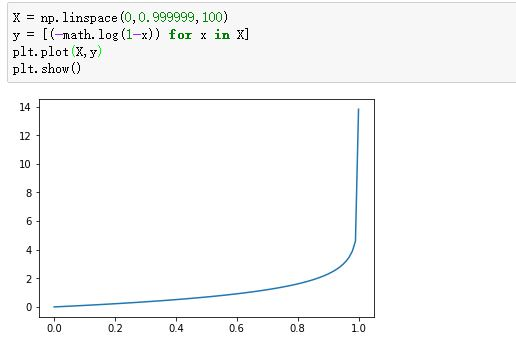
-log(1-x):
所以,我們壓縮之後,預測y在0-1之間。我們利用這個損失函式,儘量使這個損失小,就能達到很好的效果。
我們把這兩個損失綜合起來:

y就是標籤,分別取0,1,看看是不是我們前面寫的那兩個損失函式。
對於m個樣本,總的損失:
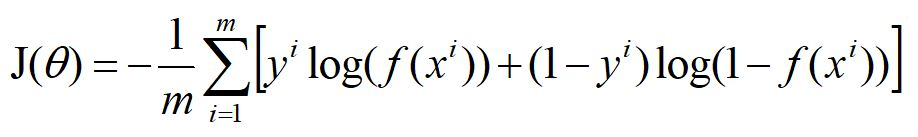
這個式子中,m是樣本數,y是標籤,取值0或1,i表示第i個樣本,f(x)表示預測的輸出。
不過,當損失過於小時,也就是模型能擬合全部/絕大部分的資料,就有可能出現過擬合。這種損失最小是經驗風險最小,為了不讓模型過擬合,我們又引入了其他的東西,來儘量減小過擬合,就是大家所說的結構風險損失。
結構經驗風險常用的是正則化,L0,L1,L2正則化
