簡單易學的機器學習演算法——Logistic迴歸
阿新 • • 發佈:2019-02-08
一、Logistic迴歸的概述
Logistic迴歸是一種簡單的分類演算法,提到“迴歸”,很多人可能覺得與分類沒什麼關係,Logistic迴歸通過對資料分類邊界的擬合來實現分類。而“迴歸”也就意味著最佳擬合。要進行最佳擬合,則需要尋找到最佳的擬合引數,一些最優化方法就可以用於最佳迴歸係數的確定。
二、最優化方法確定最佳迴歸係數
最優化方法有基於梯度的梯度下降法、梯度上升發,改進的隨機梯度下降法等等。基於梯度的優化方法在求解問題時,本身對要求解的問題有要求:即問題本身必須是可導的。其次,基於梯度的方法會使得待優化問題陷入區域性最優。此時,一些啟發式優化方法可以很好的解決這樣的問題,但是啟發式演算法的求解速度較慢,佔用記憶體較大。
對於確定迴歸係數這樣的問題
不存在多峰,也就是說不存在除最優值之外的區域性最優值。其次,這樣的問題是可求導的,所以基於梯度的方法是可以用來求解迴歸係數的問題的。優化演算法見optimal algorithm類別。
三、Sigmoid函式
當分類邊界的函式被表示出來後,可以使用一種被稱為海維塞德階躍函式(Heaviside step function)來處理,簡稱為單位階躍函式。其中Sigmoid函式是其中使用較多的一種階躍函式。Sigmoid函式如下圖:

當z為0時,函式值為0.5;
四、實驗(MATLAB程式)
1、梯度上升法
%%gradient method function weights = gradient(x, y) alpha = 0.001;%Step maxCycle = 500; [m,n] = size(x); weights = ones(n,1); for i = 1 : maxCycle h = sigmoid(x * weights); error = y - h; weights = weights + alpha * x' * error;%注意點1 end end
2、Sigmoid
%% sigmoid function
function out = sigmoid(x)
out = 1./(1+exp(-x));
end3、主程式
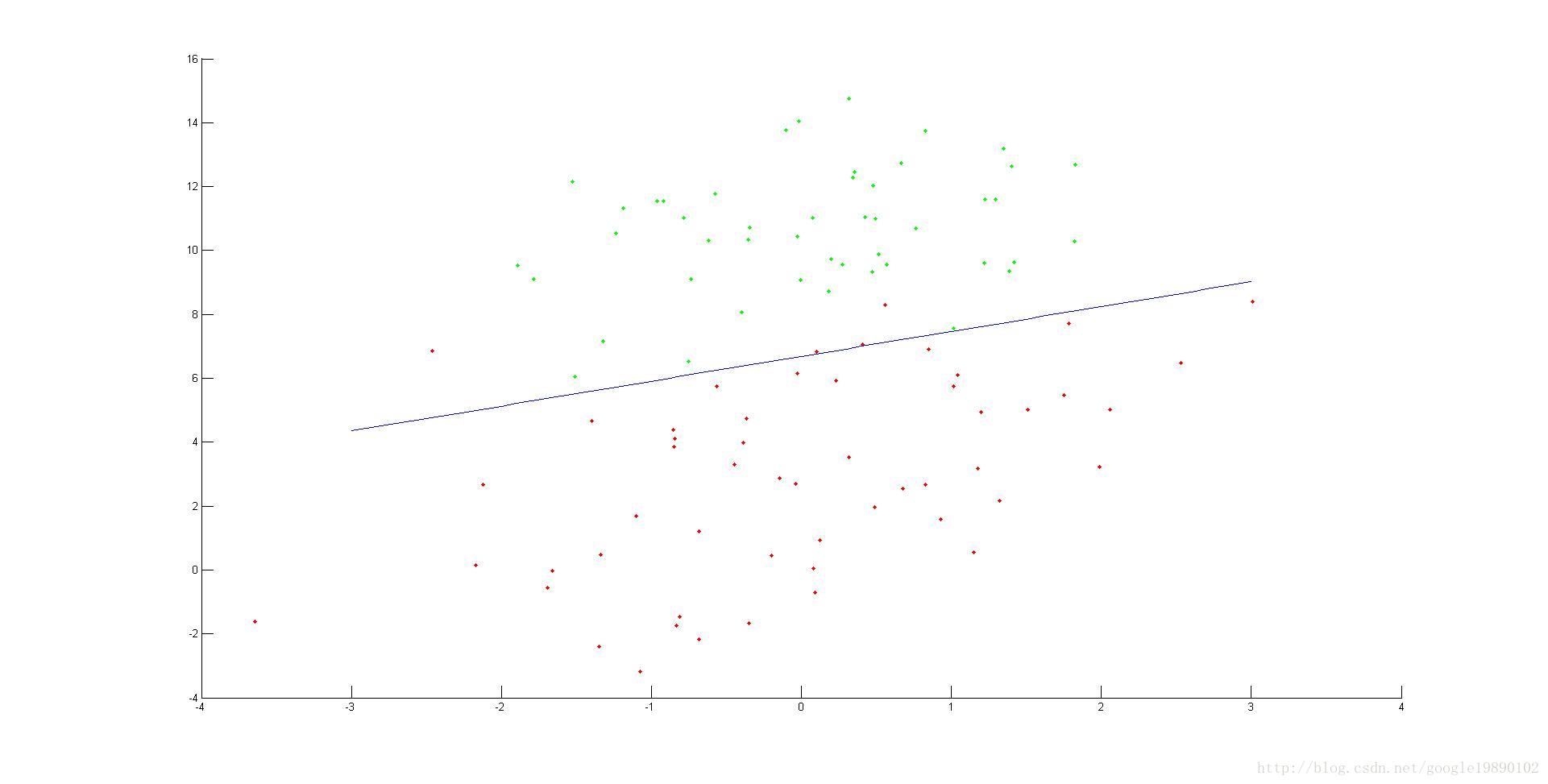
%----start----- data = load('testSet.txt');%匯入資料 [m,n] = size(data);%行和列 o = ones(m,1); dataX = data(:,1:2); X = [o,dataX]; Y = data(:,3); %--experiments-- weights = gradient(X,Y); %% plot the pic Ypic = X * weights; x_1 = X(:,2); x_2 = X(:,3); hold on for i = 1 : 100 if Y(i,:) == 0 plot(x_1(i,:),x_2(i,:),'.g'); else plot(x_1(i,:),x_2(i,:),'.r'); end end x = -3.0:0.1:3; y = (-weights(1)-weights(2)*x)/weights(3);%注意點2 plot(x,y);
4、測試的資料以及最終的分類