一、什麼是數字訊號處理？

  任何攜帶資訊的物理量都可稱為訊號。我們的日產生活中到處都充滿了訊號，其中，有些訊號是自然的，有些訊號是人為的，有些訊號是必需的（如語音訊號），有些訊號是讓人愉悅的（如音樂訊號），當然還有些訊號是不需要的，甚至是有害的（比如工地施工產生的噪音）。因此，從一個錯綜複雜的訊號中提取或增強有用的訊號，同時抑制其中的有害或無用的訊號，是數字訊號處理的一種最為直接而簡單的表述形式。更一般地說，訊號處理是為提取、增強、儲存和傳輸有用資訊而設計的一種運算。

  我們知道現實世界中的絕大多數訊號都是模擬訊號，比如語音、溫度、電磁波、腦電圖、心電圖等。為了要對這些訊號進行處理，我們要先將它們數字化，即必須要先將現實世界中的模擬訊號轉化成數字訊號，然後再進行濾波、頻譜分析等各種各樣的數字處理。在處理完成之後，還可能要再將數字訊號還原成模擬訊號。比如在鐳射唱盤播放系統中，先要將聲音訊號變成數字訊號儲存在鐳射唱盤上，在回放的時候又要重新還原成模擬訊號。一個典型的數字訊號處理框圖如下所示。ADC將模擬訊號轉變為數字訊號，DAC將數字訊號還原為模擬訊號。

  數字訊號處理是當前科學與工程領域最為熱門的技術之一，廣泛應用於通訊、雷達、聲吶、醫學成像和影象處理等許多領域，對人們的生產和生活帶來了許多革命性的變化和影響。

二、從模擬訊號到數字訊號

  在前面已經提到，自然界中的絕大多數訊號都是模擬訊號，為了對它們進行處理，我們首先要將模擬訊號轉換為數字訊號。在數字訊號處理中，這個過程叫做“模-數”變換（Analog-Digital,A/D）A/D變換的實現流程如下圖所示，主要包括了三個步驟：取樣、量化與編碼。

  以上三個步驟只適用於很理想的情況，但在實際應用中還有許多因素需要考慮。比如，我們在馬路上採集人說話的語音訊號時經常會引入周邊汽車鳴笛的噪聲，在取樣的過程中如何才能儘量避免噪聲和干擾訊號的混疊呢？一個比較好的方法是在取樣前新增一個預處理的過程，即抗混疊濾波器。其工作原理是利用一般不同訊號的頻率不同的特性（比如，人說話的頻率一般是4kHZ，汽車喇叭為1kHZ左右），在頻域上將噪聲訊號過濾掉。我們一般分析訊號都是在時間域上進行分析，如何將時間域上的訊號對映到頻率域呢？於是這就引入了我們熟知的連續時間訊號的傅立葉變換（FT）。

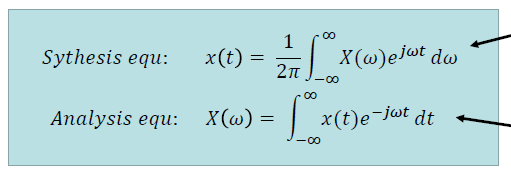
  模擬訊號在經過濾波後就可以對其進行接下來的取樣、量化與編碼操作，經過這三個步驟原先的連續時間訊號變成了離散時間訊號。

三、從數字訊號到模擬訊號

  數字化後的訊號經過一系列的訊號處理演算法之後，很多時候還需要輸出模擬訊號。這個過程通常稱為“數-模”變換（Digital-Analog,D/A），D/A變換是A/D變換的逆過程。由取樣定理可知，在滿足取樣定理的情況下，模擬訊號和對應的數字訊號完全一致。也就是說，在滿足取樣定理的情況下，從模擬訊號能得到唯一的數字訊號；反過來從數字訊號也能得到唯一的模擬訊號。（對取樣定理不夠了解的同學可參考以下連線中的博文：https://blog.csdn.net/qq_35771020/article/details/83959339）由數字訊號得到模擬訊號的過程有時也稱為重構。從頻譜的角度可以更好地理解數字訊號的重構。如下圖所示。

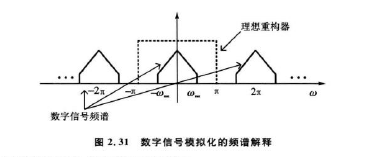
  由取樣定理的證明我們知道，數字訊號的頻譜是週期延拓的。理想情況下將數字訊號通過一個理想的低通濾波器，即可得到模擬訊號的頻譜。為實現這個過程，我們需要將取樣得到的離散時間訊號從時域變換到頻域進行分析，於是引入了離散時間傅立葉變換（DTFT）：

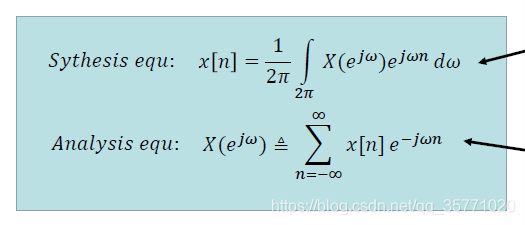
  但遺憾的是經過離散時間傅立葉變換得到的訊號頻譜是連續的，用計算機處理還是很不方便，因此在工程上難以使用。如果能將離散訊號的頻譜也變成離散的，那麼計算機處理起來將會高效很多。我們知道周期函式的頻譜是離散的，離散函式的頻譜是週期的，如果將離散函數週期化，那麼我們將得到同樣離散週期的頻譜。基於這個原理，工程師們在實際的數字訊號處理中引入了離散傅立葉變換（DFT）

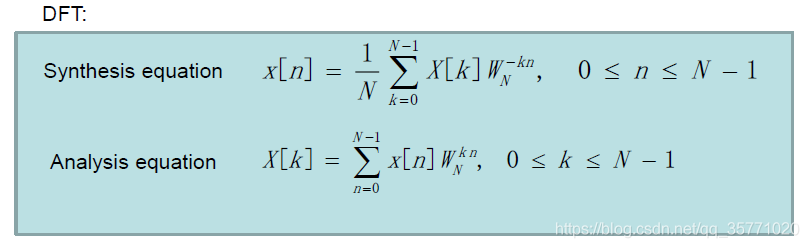
對訊號進行DFT變換得到其離散週期的頻譜後，我們從頻譜中截取出一個週期，然後對其進行傅立葉反變換，得到原始訊號發生週期延拓的週期訊號，然後從這個週期訊號中截取出一個週期即恢復出了原始訊號。

至此，整個數字訊號處理流程全部結束。