影象處理與分析(數字影象處理第二版)學習筆記(4.1)
第四章,頻率域影象增強
1,連續和離散傅立葉變換和反變換表示式?
一維連續:
二維連續:
一維離散:
二維離散:
2,二維影象離散傅立葉變換性質?
1、時移性
![]()
2、頻移性

3、均值
![]()
4、共軛對稱性
![]()
5、週期性
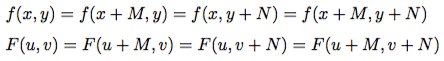
6、位移不變性是指輸入訊號的位移對於輸出訊號不會產生什麼影響,只會使得輸出訊號產生相應的位移。也就是說,如果輸入訊號為x[n]時,系統產生的輸出訊號為 y[n],那麼對於任意的輸入訊號和常數s,都有輸入訊號為x[n+s]時輸出訊號為y[n+s]成立。通過給變數n加上常數s,可以使波形在水平方向上左移或右移,注意左'+'右'-'。
7、線性
![]()
8、微分特性
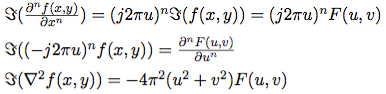
9、卷積定理
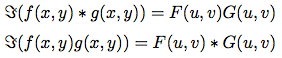
10、相關定理
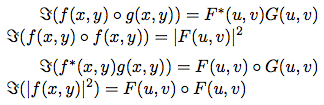
11、相似性
![]()
12、幾種特殊函式的傅立葉變換
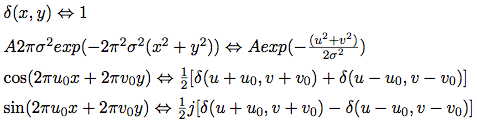
參考書籍:
《數字影象處理第二版(岡薩雷斯)》
相關推薦
影象處理與分析(數字影象處理第二版)學習筆記(5.1)
第五章,影象復原 1,什麼是影象復原? 影象復原是利用某種先驗知識來重建或者復原被退化的影象。一般來講,影象復原就是將退化模型化,並且採用相反的過程進行處理,以便復原出原影象。 2,影象退化模型表達形式? 退化過程模型化之後為一個退化函式和一個加性噪聲項。 g(x,y)=h(
影象處理與分析(數字影象處理第二版)學習筆記(4.2)
第四章 頻率域增強 1,頻率域中濾波基礎? 頻率域濾波基礎根據傅立葉變換的平移性質:當u0=M/2,v0=N/2根據尤拉公式可化為 :. 第一步,將輸入的原影象乘以(-1)^(x+y)進行中心變換; 第二步,計算變換後圖像的DFT(離散傅立葉變換); 第三步,用濾波函式H(u
影象處理與分析(數字影象處理第二版)學習筆記(4.1)
第四章,頻率域影象增強 1,連續和離散傅立葉變換和反變換表示式? 一維連續: 二維連續: &n
影象處理與分析(岡薩雷斯第二版)學習筆記(六)
第六章,彩色影象處理 1,影象的色彩空間表示形式和通道含義? 全色彩空間馬蹄圖,中間範圍分別為彩色監視器和彩色列印裝置顯示器典型色域。 ①RGB彩色模型: RGB(紅綠藍)是依據人眼識別的顏色定義出的空間,可表示大部分顏色。 R分量:紅色分量;
影象處理與分析(岡薩雷斯第二版)學習筆記(三)
第三章,空間域影象增強 1,空間域影象增強的含義? 空間域影象增強是指增強構成影象的畫素。空間域方法是直接對畫素進行操作的過程:可以由下面公式表示: g(x,y)=T[f(x,y)],其中f(x,y)為輸入影象,g(x,y)為處理後的影象,T是對f的一種操作,其定義在(x,y)的鄰域
影象處理與分析(岡薩雷斯第二版)學習筆記(二)
第二章,數字影象基礎 1,人眼視覺原理? 眼球適當聚焦,眼睛外部的光在視網膜上成像。視網膜表面的光接收器:錐狀體和桿狀體。每隻眼睛的錐狀體數目在600萬到700萬之間,主要位於視網膜中間部分,被稱為中央凹(大概1.5mm凹坑相當於1.5*1.5的方形感測器陣列),對顏色敏感度很高,可以充
前端技術(JQuery)學習筆記(一)JQuery文件準備就緒事件、JQuery事件處理、JQuery物件與DOM物件的、JQuery取值
一、JQuery,是一套JavaScript的函式庫(類庫),可以很大程度上簡化js程式碼。所以,利用Jquery對HTML元素的操作更加的便捷。 1、JQuery的核心函式:jQuery()函式,利用這個核心函式可以完成html元素的選取功能
OpenCV(Python)學習筆記(One):幾何變換之對影象的旋轉
最近學習中會用到OpenCV,感覺OpenCV簡單且功能強大,Python語言也簡單易用,於是就學了Python版OpenCV。裡面講的比較簡單,就先從簡單的入手吧。 因為已經學習一段時間了,所以文章並不是按照OpenCV的順序來寫的,我會慢慢補齊以前學過的一些例子。 都是些簡單
機器學習(西瓜書)學習筆記(一)---------模型評估與選擇
1、經驗誤差與過擬合 經驗誤差:一般的,我們把學習器的實際預測輸出與樣本的真實輸出之間的差異稱為“誤差”,學習器在訓練集上的誤差稱為“訓練誤差”或“經驗誤差”,在新樣本上的誤差稱為“泛化誤差”; 通常我們想要的一個學習器是能夠通過訓練樣本的學習後能較準確的
算法(第四版)學習筆記(二)——初級排序算法
space 倒序 優勢 name 算法 turn 資料 eply n) 時間復雜度(Time Complexity): 總運算次數表達式中受n的變化影響最大的那一項(不含系數)(註:若算法中語句執行次數為一個常數,則時間復雜度為O(1)) 若T(n)/f(n)求極限可得
數據結構(java版)學習筆記(序章)
簡單 size com bsp 一個 隊列 我們 程序 http 程序=數據結構+算法 序章做一個簡單的思維導圖,方便理解數據結構這門課的大綱,接下來我們將是按照線性表,棧,隊列,串,樹和圖的順序依次往下學。 數據結構(java版)學習筆記(序章)
OSPF網路設計解決方案(第二版)學習筆記(一)
VLSM和CIDR VLSM是通過將網路劃分為多個子網提供更大的靈活性。 ------------ 設計VLSM的使用幫助指導方針 1、最佳的彙總應該鄰近的塊地址之間 2、如果小的子網被聚合,則路由選擇資訊可以彙總 3、將VLSM子網聚合起來以便路由選擇資訊統一 4、通過將一個子網進一步劃分子網
Linux(CentOS)學習筆記(一)——Linux命令
一、Linux基本原則 一切皆檔案 配置檔案儲存為純文字格式 二、使用者介面(shell):應用程式 GUI介面(Graphic User Interface圖形使用者介面) - Windows:explorer.exe - centos:KDE CLI介
Linux(CentOS)學習筆記(四)——Linux命令
vi和vim命令 vi是一個文字編輯程式,不是排版工具,不過命令繁多而且功能強大,在簡單版的Linux系統中是沒有預裝vim的,vim跟vi相比,多了特殊字元的顏色區分。 Vi有三種基本工作模式: - 命令模式 - 文字輸入模式 - 末行模式 命令列模
機器學習(西瓜書)學習筆記(四)---------神經網路
1. 神經元模型 神經網路/人工神經網路:由具有適應性的簡單單元組成的廣泛並行互連的網路。 神經網路學習:機器學習和神經網路兩個學科交叉的部分。 Neural Networks中的基本單元:神經元。 從電腦科學的角度,NN就是一個包含了大量引數的數學模型,該模型由若干個函式相互代入而
機器學習(西瓜書)學習筆記(三)---------決策樹
1、基本流程 決策樹通常從一個最基本的問題出發,通過這個判定問題來對某個“屬性”進行“測試”,根據測試的結果來決定匯出結論還是匯出進一步的判定問題,當然,這個判定範圍是在上次決策結果的限定範圍之內的。 出發點
機器學習(西瓜書)學習筆記(二)---------線性模型
1、基本形式 對含有d個特徵的資料x,線性模型試圖學得一個通過特徵的線性組合來進行預測的函式:
資料庫課設(圖書管理系統)學習筆記(1)
圖書館課課設圖片插入,讀出 BufferedImage: 所述BufferedImage亞類描述了一種Image與影象資料的訪問的緩衝器。 A BufferedImage由影象資料的ColorModel和Raster組成。 SampleModel中SampleModel中的Raster的
DOM(文件物件模型)學習筆記(一)
DOM可以將任何Html或XML文件描繪成一個由多層節點構成的結構,節點分為多種型別,每個節點都有自己的特點,資料和方法。 ** Node型別: ** 每個節點都有一個nodeType屬性,表明節點的型別,nodeName屬性表示元素的標
模式識別(Pattern Recognition)學習筆記(三十六)-- 動態聚類演算法
如果不估計樣本的概率分佈,就無法從概率分佈的角度來定義聚類,這時我們就需要有一種新的對聚類的定義,一般的,根據樣本間的某種距離或某種相似性度量來定義聚類,即把相似的或距離近的樣本聚為一類,而把不相似或距離遠的樣本聚在其他類,這種基於相似性度量的聚類方法在實際應用中非常常用,
