【演算法筆記 - 1】多項式乘法 —— FFT
目錄
- @0 - 參考資料@
- @1 - 一些概念@
- @2 - 傅立葉正變換@
- @3 - 傅立葉逆變換@
- @4 - 迭代實現 [email protected]
- @5 - 參考程式碼實現@
- @6 - 快速數論變換 [email protected]
@0 - 參考資料@
@1 - 一些概念@
多項式的係數表示法:形如 \(A(x)=a_0+a_1x+...+a_{n-1}x^{n-1}\)。
多項式的點值表示法:對於 n-1 次多項式 \(A(x)\),我們選取 n 個不同的值 \(x_0, x_1, ... , x_{n-1}\)
把多項式係數當作 n 個變數,n 個點當作 n 個線性方程,可以用高斯消元來求得唯一解。因此,我們可以用這 n 個點唯一表示 A(x) 。
注意,一個多項式的點值表示法並不是唯一的。
如果用點值表示法的多項式作乘法,可以直接把縱座標相乘,在 O(n) 的時間實現多項式乘法。
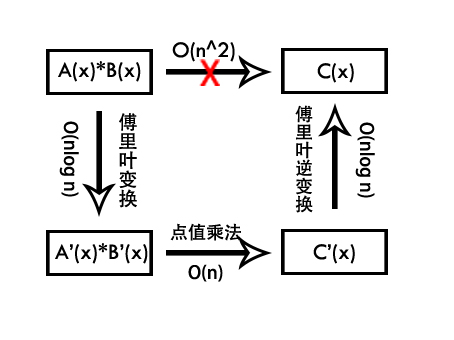
FFT(快速傅立葉變換)可以實現 O(nlog n) 的 點值表示 與 係數表示 之間的轉換。
一個解釋多項式乘法原理的圖:
複數:複數簡單來說就是 \(a + bi\)
複數的乘法可以直接(a + bi)(c + di)展開相乘。但是幾何上覆數乘法還有另一種解釋:
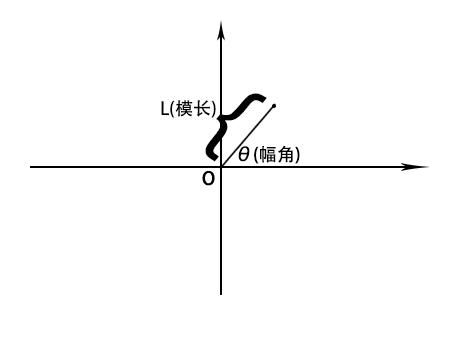
這樣定義下,複數的乘法為模長相乘,幅角相加。
單位根:定義 n 次單位根為使得 \(z^n=1\) 成立的複數 \(z\)。一共 n 個,在單位圓上且 n 等分單位圓。
可以發現 n 次單位根模長都為 1,幅角依次為\(0*\frac{2\pi}{n},1*\frac{2\pi}{n},...,(n-1)*\frac{2\pi}{n}\)。
我們記 n 次單位根依次為\(w_n^0,w_n^1,...w_n^{n-1}\)
有以下幾個性質:
(1)\(w_{n}^{i}*w_{n}^{j}=w_{n}^{i+j}\)
(2)\(w_{dn}^{dk}=w_n^k\),有點類似於分數的約分。
(3)\(w_{2n}^k=-w_{2n}^{k+n}\)。
以上幾個性質都可以從幅角的方面去理解。
@2 - 傅立葉正變換@
FFT 的正變換實現,是基於對多項式進行奇偶項分開遞迴再合併的分治進行的。
對於 n-1 次多項式,我們選擇插入 n 次單位根求出其點值表示式。
記多項式\(A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\)。
再記\(A_o(x)=a_1+a_3x+a_5x^2+...\)。
再記\(A_e(x)=a_0+a_2x+a_4x^2+...\)。
有\(A(x)=x*A_o(x^2)+A_e(x^2)\)。
令 \(n = 2*p\)。則有:
\(A(w_n^k)=w_n^k*A_o[(w_{n/2}^{k/2})^2]+A_e[(w_{n/2}^{k/2})^2]=w_n^k*A_o(w_p^k)+A_e(w_p^k)\);
\(A(w_n^{k+p})=w_n^{k+p}*A_o(w_p^{k+p})+A_e(w_p^{k+p})=-w_n^k*A_o(w_p^k)+A_e(w_p^k)\)
在已知 \(A_o(w_p^k)\) 與 \(A_e(w_p^k)\) 的前提下,可以 O(1) 算出 \(A(w_n^k)\) 與 \(A(w_n^{k+p})\)。
因此,假如我們遞迴求解 \(A_o(x),A_e(x)\) 兩個多項式 p 次單位根的插值,就可以在O(n)的時間內算出 \(A(x)\) n 次單位根的插值。
時間複雜度是經典的 \(T(n)=2*T(n/2)+O(n)=O(n\log n)\)。
@3 - 傅立葉逆變換@
觀察我們剛剛的插值過程,實際上就是進行了如下的矩陣乘法。
\(\begin{bmatrix} (w_n^0)^0 & (w_n^0)^1 & \cdots & (w_n^0)^{n-1} \\ (w_n^1)^0 & (w_n^1)^1 & \cdots & (w_n^1)^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{n-1})^0 & (w_n^{n-1})^1 & \cdots & (w_n^{n-1})^{n-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} A(w_n^0) \\ A(w_n^1) \\ \vdots \\ A(w_n^{n-1}) \end{bmatrix}\)
我們記上面的係數矩陣為 \(V\)。
對於下面定義的 \(D\):
\(D = \begin{bmatrix} (w_n^{-0})^0 & (w_n^{-0})^1 & \cdots & (w_n^{-0})^{n-1} \\ (w_n^{-1})^0 & (w_n^{-1})^1 & \cdots & (w_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{-(n-1)})^0 & (w_n^{-(n-1)})^1 & \cdots & (w_n^{-(n-1)})^{n-1} \end{bmatrix}\)
考慮 \(D*V\)的結果:
\((D*V)_{ij}=\sum_{k=0}^{k<n}d_{ik}*v_{kj}=\sum_{k=0}^{k<n}w_n^{-ik}*w_{n}^{kj}=\sum_{k=0}^{k<n}w_n^{k(j-i)}\)
當 i = j 時,\((D*V)_{ij}=n\);
當 i ≠ j 時,\((D*V)_{ij}=1+w_n^{j-i}+(w_n^{j-i})^2+...=\frac{1-(w_n^{j-i})^n}{1-w_n^{j-i}}\)=0;
【根據定義,n 次單位根的 n 次方都等於 1】
所以:\(\frac1n*D=V^{-1}\)
因此將這個結果代入最上面那個公式裡面,有:
\(\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \frac1n \begin{bmatrix} (w_n^{-0})^0 & (w_n^{-0})^1 & \cdots & (w_n^{-0})^{n-1} \\ (w_n^{-1})^0 & (w_n^{-1})^1 & \cdots & (w_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{-(n-1)})^0 & (w_n^{-(n-1)})^1 & \cdots & (w_n^{-(n-1)})^{n-1} \end{bmatrix}\begin{bmatrix} A(w_n^0) \\ A(w_n^1) \\ \vdots \\ A(w_n^{n-1}) \end{bmatrix}\)
“這樣,逆變換 就相當於把 正變換 過程中的 \(w_n^k\) 換成 \(w_n^{-k}\),之後結果除以 n 就可以了。”——摘自某部落格。
……
還是有點難理解。比如為什麼我們不直接把\(w_n^k\) 換成 \(\frac1n*w_n^{-k}\) 算了。
實際上,因為\(w_n^{-k}=w_n^{n-k}\),也就是說它 TM 還是一個 n 次單位根。所以我們插值還是正常的該怎麼插怎麼插。如果換成 \(\frac1n*w_n^{-k}\) 它就不是一個單位根,以上性質就不滿足了。
@4 - 迭代實現 [email protected]
遞迴版本的 FFT 雖好,可奈何常數太大。
我們考慮怎麼迭代實現 FFT。觀察奇偶分組後各數的位置。
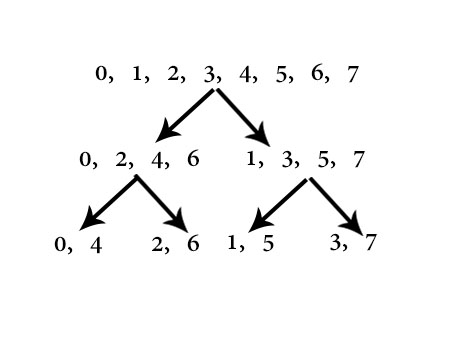
原序列:0,1,2,3,4,5,6,7。
終序列:0,4,2,6,1,5,3,7。
轉換為二進位制再來看看。
原序列:000,001,010,011,100,101,110,111。
終序列:000,100,010,110,001,101,011,111。
可以發現終序列是原序列每個元素的翻轉。
於是我們可以先把要變換的係數排在相鄰位置,從下往上迭代。
這個二進位制翻轉過程可以自己腦補方法,只要保證時間複雜度O(nlog n),程式碼簡潔就可以了。
在這裡給出一個參考的方法:
我們對於每個 i,假設已知 i-1 的翻轉為 j。考慮不進行翻轉的二進位制加法怎麼進行:從最低位開始,找到第一個為 0 的二進位制位,將它之前的 1 變為 0,將它自己變為 1。因此我們可以從 j 的最高位開始,倒過來進行這個過程。
@5 - 參考程式碼實現@
本程式碼為 uoj#34 的AC程式碼。在程式碼中有些細節可以關注一下。
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 400000;
const double PI = acos(-1);
struct complex{
double r, i;
complex(double _r=0, double _i=0):r(_r), i(_i){}
};//C++ 有自帶的複數模板庫,但很顯然我並不會。
typedef complex cplx;
cplx operator +(cplx a, cplx b){return cplx(a.r+b.r, a.i+b.i);}
cplx operator -(cplx a, cplx b){return cplx(a.r-b.r, a.i-b.i);}
cplx operator *(cplx a, cplx b){return cplx(a.r*b.r-a.i*b.i, a.r*b.i+b.r*a.i);}
void FFT(cplx *A, int n, int type) {
for(int i=0,j=0;i<n;i++) {
if( i < j ) swap(A[i], A[j]);
for(int k=(n>>1);(j^=k)<k;k>>=1);//這個地方讀不懂就背吧。。。
}
for(int s=2;s<=n;s<<=1) {
int t = (s>>1);
cplx u = cplx(cos(type*PI/t), sin(type*PI/t));
//這個地方需要注意一點:如果題目中需要反覆用到 FFT,則可以預處理出所有單位根以減小常數。
for(int i=0;i<n;i+=s) {
cplx r = cplx(1, 0);
for(int j=0;j<t;j++,r=r*u) {
cplx e = A[i+j], o = A[i+j+t];
A[i+j] = e + r*o; A[i+j+t] = e - r*o;
}
}
}
}
cplx A[MAXN + 5], B[MAXN + 5], C[MAXN + 5];
int main() {
int n, m;
scanf("%d%d", &n, &m); n++, m++;
for(int i=0;i<n;i++)
scanf("%lf", &A[i].r);
for(int i=0;i<m;i++)
scanf("%lf", &B[i].r);
int len = 1;
while( len < (n+m-1) ) len <<= 1;
//此處重點:由於我們每一次都要奇偶分組,所以長度必須為2的整數次冪,高位補0就好了。
FFT(A, len, 1); FFT(B, len, 1);
for(int i=0;i<len;i++)
C[i] = A[i] * B[i];
FFT(C, len, -1);
for(int i=0;i<n+m-1;i++)
printf("%d ", int(round(C[i].r/len)));//記得,一定要記得除以len。
}@6 - 快速數論變換 [email protected]
實際上這可以算是 FFT 的一個優化。
FFT雖然跑得快,但是因為是浮點數運算,終究還是有 精度、常數 等問題。
然而問題來了:我們多項式乘法都是整數在那裡搞來搞去,為什麼一定要扯到浮點數。是否存在一個在模意義下的,只使用整數的方法?
想一想我們用了哪些單位根的性質:
(1)\(w_{n}^{i}*w_{n}^{j}=w_{n}^{i+j}\)
(2)\(w_{dn}^{dk}=w_n^k\)
(3)\(w_{2n}^k=-w_{2n}^{k+n}\)
(4) n 個單位根互不相同,且 \(w_n^0=1\)
我們能否找到一個數,在模意義下也滿足這些性質?
引入原根的概念:對於素數 p,p 的原根 G 定義為使得 \(G^0,G^1,...,G^{p−2}(\mod p)\) 互不相同的數。
再定義 \(g_n^k = (G^{\frac{p-1}{n}})^k\)。驗證一下這個東西是否滿足單位根的以上性質。
(1),由冪的運算立即可得。
(2),由冪的運算立即可得。
(3),\(g_{2n}^{k+n}=(G^{\frac{p-1}{2n}})^{k+n}=(G^{\frac{p-1}{2n}})^k*(G^{\frac{p-1}{2n}})^n=G^{\frac{p-1}{2}}*g_{2n}^k=-g_{2n}^k(\mod p)\)。
【因為\(G^{p-1}=1(\mod p)\)且由原根定義\(G^{\frac{p-1}{2}}\not=G^{p-1}(\mod p)\),故\(G^{\frac{p-1}{2}}=-1(\mod p)\)】
(4),由原根的定義立即可得。
所以我們就可以搞 NTT 了。直接把程式碼中涉及單位根的換成原根即可。
然而,可以發現 NTT 適用的模數 m 十分有限。它應該滿足以下性質:
(1)令 \(m = 2^p*k+1\),k 為奇數,則多項式長度必須 \(n \le 2^p\)。
(2)方便記憶,方便記憶,與方便記憶。
這裡有一些合適的模數【來源:miskcoo】。
