RSA演算法的C++string實現(模冪演算法和歐幾里得演算法的使用)後附思路
阿新 • • 發佈:2018-12-23
void resetNumA(string numAStr); //使用string重置numB void resetNumB(string numBStr); //將陣列轉換為字串,用於輸出 string getNumString(int* num); //判斷兩個數字哪個大 int compare(string numAStr, string numBStr); //加法 string sum(string numAStr, string numBStr); //減法 string sub(string numAStr, string numBStr); //乘法 string mul(string numAStr, stringnumBStr); //除 string div(string numAStr, string numBStr); //取餘 string mod(string numAStr, string numBStr); //模冪演算法 string getMod(string m, string pow, string n); //求2的n次方函式 string mul_2(int i); //求m的n次方 string mul_m(string m, string n); #endif
#include<iostream> #include"operation.h" #include<string> #include<vector> using namespace std; //結果支援的最大位數 const static int M = 2000; int numA[M]; int numB[M]; //使用string重置numA void resetNumA(string numAStr) { memset(numA, 0, M * sizeof(int)); //將字串的每一位都轉換成數字傳入陣列 for (int i = 0; i < numAStr.length(); i++) { numA[i] = numAStr[numAStr.length() - i - 1] - '0'; } } //使用string重置numB void resetNumB(string numBStr) { memset(numB, 0, M * sizeof(int)); //將字串的每一位都轉換成數字傳入陣列 for (int i = 0; i < numBStr.length(); i++) { numB[i] = numBStr[numBStr.length() - i - 1] - '0'; } } //將陣列轉換為字串,用於輸出 string getNumString(int* num) { string numString; bool isBegin = false; for (int i = M - 1; i >= 0; i--) { if (num[i] != 0) { isBegin = true; } if (isBegin) { numString += num[i] + '0'; } } return numString; } //判斷兩個數字哪個大 int compare(string numAStr, string numBStr) { int i = 0; int la = 0; while (numAStr[i] == '0') { la++; i++; } i = 0; int lb = 0; while (numBStr[i] == '0') { lb++; i++; } string a(numAStr.substr(la, numAStr.length())); string b(numBStr.substr(lb, numBStr.length())); if (a.length() > b.length()) { return 1; } else if (a.length() < b.length()) { return -1; } else { for (int i = 0; i < a.length(); i++) { if (a[i]>b[i]) { return 1; } if (a[i]<b[i]) { return -1; } } return 0; } } //加法 string sum(string numAStr, string numBStr) { resetNumA(numAStr); resetNumB(numBStr); for (int i = 0; i < M; i++) { //結果儲存在numA中 numA[i] += numB[i]; //數字大於9則進位 if (numA[i]>9) { numA[i] -= 10; numA[i + 1]++; } } return getNumString(numA); } //減法 string sub(string numAStr, string numBStr) { bool isNegative = false; //如果numA比numB小 //則結果為負數 //調換位置進行計算 if (compare(numAStr, numBStr) == -1) { isNegative = true; string temp = numAStr; numAStr = numBStr; numBStr = temp; } else if (compare(numAStr, numBStr) == 0) { return "0"; } resetNumA(numAStr); resetNumB(numBStr); for (int i = 0; i < M; i++) { //減數小於被減數就借位 if (numA[i]<numB[i]) { numA[i] = numA[i] + 10 - numB[i]; numA[i + 1]--; } else { numA[i] -= numB[i]; } } if (isNegative) { return "-" + getNumString(numA); } else { return getNumString(numA); } } //乘法 string mul(string numAStr, string numBStr) { resetNumA(numAStr); resetNumB(numBStr); vector<string> nums; for (int i = 0; i < numBStr.length(); i++) { //初始化一個臨時資料來儲存被乘數與乘數的某一位相乘的結果 int temp[M]; memset(temp, 0, M * sizeof(int)); for (int j = i; j < numAStr.length() + i; j++) { temp[j] += numA[j - i] * numB[i] % 10; temp[j + 1] = numA[j - i] * numB[i] / 10; //如果大於9,那麼就做進位處理 if (temp[j]>9) { temp[j] -= 10; temp[j + 1]++; } } nums.push_back(getNumString(temp)); } //每位相乘的結果再用加法加起來 string result = nums[0]; for (int i = 1; i < nums.size(); i++) { result = sum(result, nums[i]); } return result; } //除,結果精確到個位 string div(string numAStr, string numBStr) { resetNumA(numAStr); resetNumB(numBStr); string result; string left; if (compare(numAStr, numBStr) == -1) { return "0"; } //標記第一個不為0的位數的出現 bool flag = false; for (int i = 0; i < numAStr.length(); i++) { left += numAStr[i]; //餘數比除數大 if (compare(left, numBStr) == 1) { flag = true; int count = 1; string temp = numBStr; while (true) { //每迴圈一次加上一個餘數 temp = sum(temp, numBStr); //餘數仍然大於除數,繼續累加 if (compare(left, temp) == 1) { count++; } //餘數小於除數 //可以計算結果 else if (compare(left, temp) == -1) { result += count + '0'; left = sub(left, sub(temp, numBStr)); break; } //此時餘數剛好是除數的倍數 else if (compare(left, temp) == 0) { count++; result += count + '0'; left = ""; break; } } } //剛好除盡 else if (compare(left, numBStr) == 0) { flag = true; result += "1"; left = ""; } //餘數比除數小,跳到下一位 else if (flag) { result += "0"; } } return result; } //取模 string mod(string numAStr, string numBStr) { string result = "0"; if (compare(numAStr, numBStr) == -1) { return numAStr; } else if (compare(numAStr, numBStr) == 0) { return result; } else { string d = div(numAStr, numBStr); string x = mul(numBStr, d); result = sub(numAStr, x); return result; } } //加密解密模冪演算法 string getMod(string m, string pow, string n) { string temp; while (compare(pow,"1") == 1) { if(mod(pow,"2")=="1") temp = temp + "1"; else temp = temp + "0"; pow = div(pow,"2"); } temp = temp + "1"; int length = temp.length(); string T[M]; string M = "1"; T[0] = mod(m, n); for (int i = 1; i < length; i++) { T[i] = mod(mul(T[i-1],T[i-1]),n); } for (int i = 0; i < length; i++) { if (temp[i] == '1') { M = mul(M, T[i]); } } string result = mod(M, n); return result; } //求2的n次方函式 string mul_2(int i) { string result = "2"; for (int j = 1; j < i; j++) { result = mul(result, "2"); } if (i == 0) return "1"; else return result; } //求m的t次方函式 string mul_m(string m,string t) { string result = m; string j; for ( j = "1"; compare(j, t) == -1; j = sum(j, "1")) { result = mul(result, m); } return result; }
#include<iostream> #include"operation.h" using namespace std; int main() { string char_number_p; string char_number_q; string temp[3000][4]; //p=17,q=11 //p=17,q=19 //p=41,q=43 //67,71 //797 809 //49993 49999 //116747 110221 //1000017077 //141008192341187 char_number_p="100010001707701"; char_number_q="141008192341187"; string n = mul(char_number_p, char_number_q); string tmp1 = "1"; string On = mul(sub(char_number_p, tmp1),sub(char_number_q, tmp1)); string e = "65537"; //拓展歐幾里得演算法 temp[0][0] = e; temp[0][1] = ""; temp[0][2] = On; temp[0][3] = ""; int i = 1; do { temp[i][0] = temp[i - 1][0]; temp[i][1] = ""; temp[i][2] = temp[i - 1][2]; temp[i][3] = ""; if (compare(temp[i][0], temp[i][2]) == 1) { temp[i][0] = mod(temp[i][0], temp[i][2]); } else { temp[i][2] = mod(temp[i][2], temp[i][0]); } i++; } while (compare(temp[i - 1][0], "1") == 1); int value = i - 1; temp[value][1] = "1"; value--; while (value >= 0) { if (temp[value + 1][1] != "") temp[value][3] = div(sub(mul(temp[value][0], temp[value + 1][1]), "1"), temp[value][2]); else if (temp[value + 1][3] != "") temp[value][1] = div(sum(mul(temp[value][2], temp[value + 1][3]), "1"), temp[value][0]); value--; } string d = temp[0][1]; cout << "e:" << e << endl; cout << "p*q:" << n << endl; cout << "O(n):" << On << endl; cout << "d:" << d << endl; cout << "金鑰{ " << e << " , " << n << " }" << endl; cout << "公鑰{ " << d << " , " << char_number_p <<" , "<< char_number_q << " }" << endl; string miwen; cout << "請輸入密文(暫小於10的29次方)" << endl; cin >> miwen; cout << "密文:" << miwen << endl; string C1 = getMod(miwen, e, n); cout << "加密後的明文:" << C1 << endl; string M1 = getMod(C1, d, n); cout << "解密後的密文:" << M1 << endl; cout << "請輸入密文(暫小於10的29次方)" << endl; cin >> miwen; string C2 = getMod(miwen, e, n); cout << "加密後的明文:" << C2 << endl; string M2 = getMod(C2, d, n); cout << "解密後的密文:" << M2 << endl; cout << "請輸入密文(暫小於10的29次方)" << endl; cin >> miwen; string C3 = getMod(miwen, e, n); cout << "加密後的明文:" << C3 << endl; string M3 = getMod(C3, d, n); cout << "解密後的密文:" << M3 << endl; system("pause"); return 0; }
以上為測試實現的程式碼。
思路:先實現string型別的加減乘除的重寫,以及用到的其他的操作函式,比較,取模,加解密函式,以及其他的m的n次方的操作。
然後在主函式裡面嵌入歐幾里得演算法,呼叫求得d,之後就是簡單的呼叫加解密函式
pq的值也是測試得到的
這是執行截圖:
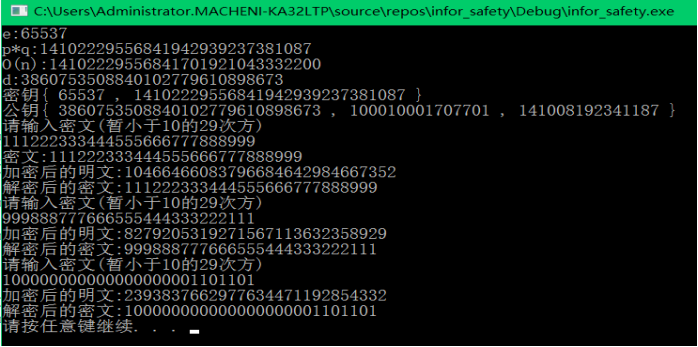
//拓展歐幾里得演算法
temp[0][0] = e;
temp[0][1] = "";
temp[0][2] = On;
temp[0][3] = "";
int i = 1;
do { temp[i][0] = temp[i - 1][0]; temp[i][1] = ""; temp[i][2] = temp[i - 1][2]; temp[i][3] = ""; if (compare(temp[i][0], temp[i][2]) == 1) { temp[i][0] = mod(temp[i][0], temp[i][2]); } else { temp[i][2] = mod(temp[i][2], temp[i][0]); } i++; } while (compare(temp[i - 1][0], "1") == 1); int value = i - 1; temp[value][1] = "1"; value--; while (value >= 0) { if (temp[value + 1][1] != "") temp[value][3] = div(sub(mul(temp[value][0], temp[value + 1][1]), "1"), temp[value][2]); else if (temp[value + 1][3] != "") temp[value][1] = div(sum(mul(temp[value][2], temp[value + 1][3]), "1"), temp[value][0]); value--; } string d = temp[0][1];
這部分拓展的歐幾里得演算法也可以單獨使用,這裡是用空間換取的時間效率。
