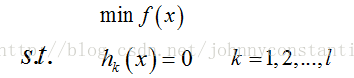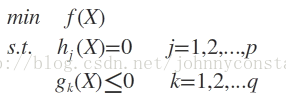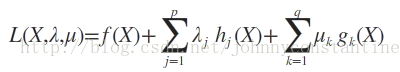在求解最優化問題中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）條件是兩種最常用的方法。在有等式約束時使用拉格朗日乘子法，在有不等約束時使用KKT條件。

　　我們這裡提到的最優化問題通常是指對於給定的某一函式，求其在指定作用域上的全域性最小值(因為最小值與最大值可以很容易轉化，即最大值問題可以轉化成最小值問題)。提到KKT條件一般會附帶的提一下拉格朗日乘子。對學過高等數學的人來說比較拉格朗日乘子應該會有些印象。二者均是求解最優化問題的方法，不同之處在於應用的情形不同。

      一般情況下，最優化問題會碰到一下三種情況：

（1）無約束條件

　　這是最簡單的情況，解決方法通常是函式對變數求導，令求導函式等於0的點可能是極值點。將結果帶回原函式進行驗證即可。

（2）等式約束條件

      設目標函式為f(x)，約束條件為h_k(x)，形如:

      　　s.t. 表示subject to ，“受限於”的意思，l表示有l個約束條件。

　　　則解決方法是消元法或者拉格朗日法。消元法比較簡單不在贅述，這裡主要講拉格朗日法，因為後面提到的KKT條件是對拉格朗日乘子法的一種泛化。

　　　例如給定橢球:

　  　求這個橢球的內接長方體的最大體積。這個問題實際上就是條件極值問題，即在條件      下，求的最大值。

　　  當然這個問題實際可以先根據條件消去 z (消元法)，然後帶入轉化為無條件極值問題來處理。但是有時候這樣做很困難，甚至是做不到的，這時候就需要用拉格朗日乘數法了。  

　　  首先定義拉格朗日函式F(x)：

　　　　　　　　  （ 其中λk是各個約束條件的待定係數。）                                                           

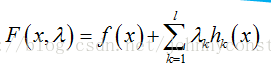
        然後解變數的偏導方程：

      　　　　......,

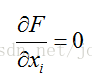
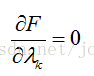
　　　如果有l個約束條件，就應該有l+1個方程。求出的方程組的解就可能是最優化值（高等數學中提到的極值），將結果帶回原方程驗證就可得到解。

　　　回到上面的題目，通過拉格朗日乘數法將問題轉化為

　　　對求偏導得到

　　　聯立前面三個方程得到和，帶入第四個方程解之

　　　帶入解得最大體積為：

（3）不等式約束條件

       設目標函式f(x)，不等式約束為g(x)，有的教程還會新增上等式約束條件h(x)。此時的約束優化問題描述如下：

        則我們定義不等式約束下的拉格朗日函式L，則L表示式為：

      其中f(x)是原目標函式，hj(x)是第j個等式約束條件，λj是對應的約束係數，gk是不等式約束，uk是對應的約束係數。

　　常用的方法是KKT條件，同樣地，把所有的不等式約束、等式約束和目標函式全部寫為一個式子L(a, b, x)= f(x) + a*g(x)+b*h(x)，

　　KKT條件是說最優值必須滿足以下條件：

　　　　1）L(a, b, x)對x求導為零；

　　　　2）h(x) =0;

　　　　3）a*g(x) = 0;

　　求取這些等式之後就能得到候選最優值。其中第三個式子非常有趣，因為g(x)<=0，如果要滿足這個等式，必須a=0或者g(x)=0. 這是SVM的很多重要性質的來源，如支援向量的概念。