[轉自：
http://www.cppblog.com/superKiki/archive/2010/05/15/115421.html]
字尾陣列
【字尾陣列是處理字串的有力工具。字尾陣列是字尾樹的一個非常精巧的替代品，它比字尾樹容易程式設計實現，能夠實現字尾樹的很多功能而時間複雜度也並不遜色，而且它比字尾樹所佔用的記憶體空間小很多。可以說，在資訊學競賽中字尾陣列比字尾樹要更為實用。】

1.1、基本定義

　　子串：字串S的子串r[i..j]，i≤j，表示r串中從i到j這一段，也就是順次排列r[i]，r[i+1]，…，r[j]形成的字串。

　　字尾：字尾是指從某個位置i開始到整個串末尾結束的一個特殊子串。字串r的從第i個字元開始的字尾表示為Suffix(i)，也就是Suffix(i)=r[i..len(r)]。

　　大小比較：關於字串的大小比較，是指通常所說的“字典順序”比較，也就是對於兩個字串u、v，令i從1開始順次比較u[i]和v[i]，如果u[i]=v[i]則令i加1，否則若u[i]<v[i]則認為u<v，u[i]>v[i]則認為u>v（也就是v<u），比較結束。如果i>len(u)或者 i>len(v)仍比較不出結果，那麼若len(u)<len(v)則認為u<v，若 len(u)=len(v)則認為u=v，若len(u)>len(v)則 u>v。

　　從字串的大小比較的定義來看，S的兩個開頭位置不同的字尾 u和v進行比較的結果不可能是相等，因為 u=v的必要條件len(u)=len(v)在這裡不可能滿足。

　　字尾陣列：字尾陣列SA是一個一維陣列，它儲存1..n的某個排列SA[1]，SA[2]，……，SA[n]，並且保證 Suffix(SA[i])<Suffix(SA[i+1])，1≤i<n。也就是將S的n個字尾從小到大進行排序之後把排好序的字尾的開頭位置順次放入SA中。

　　名次陣列：名次陣列Rank[i]儲存的是Suffix(i)在所有後綴中從小到大排列的“名次”。

　　簡單的說，字尾陣列是“排第幾的是誰？”，名次陣列是“你排第幾？”。容易看出，字尾陣列和名次陣列為互逆運算。如圖1所示。
　　
　　設字串的長度為n。為了方便比較大小，可以在字串後面新增一個字元，這個字元沒有在前面的字元中出現過，而且比前面的字元都要小。在求出名次陣列後，可以僅用O(1)的時間比較任意兩個字尾的大小。在求出字尾陣列或名次陣列中的其中一個以後，便可以用O(n)的時間求出另外一個。任意兩個字尾如果直接比較大小，最多需要比較字元n次，也就是說最遲在比較第n個字元時一定能分出“勝負”。

1.2、倍增演算法
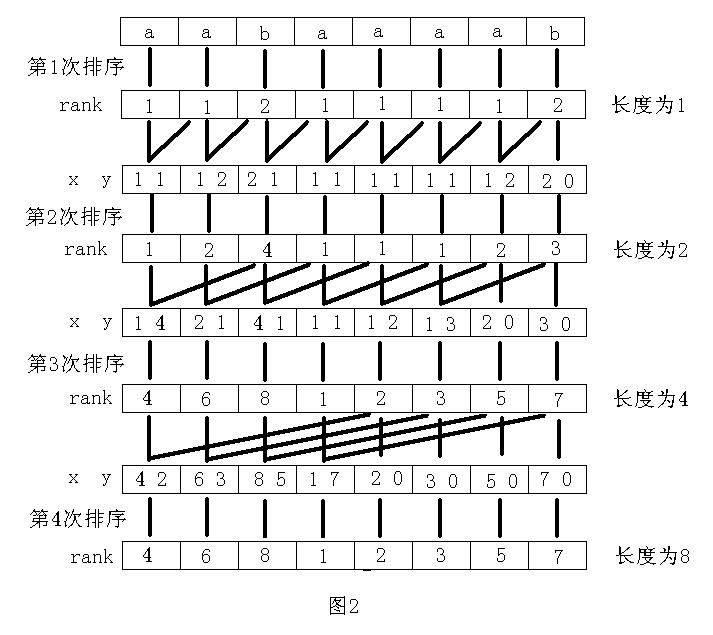
倍增演算法的主要思路是：用倍增的方法對每個字元開始的長度為2k的子字串進行排序，求出排名，即rank值。k從0開始，每次加1，當2k大於n以後，每個字元開始的長度為2k的子字串便相當於所有的字尾。並且這些子字串都一定已經比較出大小，即rank值中沒有相同的值，那麼此時的rank值就是最後的結果。每一次排序都利用上次長度為2k-1的字串的rank值，那麼長度為2k的字串就可以用兩個長度為2k-1的字串的排名作為關鍵字表示，然後進行基數排序，便得出了長度為2k的字串的rank值。以字串“aabaaaab”為例，整個過程如圖2所示。其中x、y是表示長度為2k的字串的兩個關鍵字。

具體實現：

int wa[maxn],wb[maxn],wv[maxn],ws[maxn];

int cmp(int *r,int a,int b,int l)
{return r[a]==r[b]&&r[a+l]==r[b+l];}

void da(int *r,int *sa,int n,int m)
{
    int i,j,p,*x=wa,*y=wb,*t; 
    for(i=0;i<m;i++) ws[i]=0; 
    for(i=0;i<n;i++) ws[x[i]=r[i]]++; 
    for(i=1;i<m;i++) ws[i]+=ws[i-1]; 
    for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i; 
    for(j=1,p=1;p<n;j*=2,m=p) 
    { 
        for(p=0,i=n-j;i<n;i++) y[p++]=i; 
        for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j; 
        for(i=0;i<n;i++) wv[i]=x[y[i]]; 
        for(i=0;i<m;i++) ws[i]=0; 
        for(i=0;i<n;i++) ws[wv[i]]++; 
        for(i=1;i<m;i++) ws[i]+=ws[i-1]; 
        for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i]; 
        for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++) 
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; 
    } 
    return; 
}

　　待排序的字串放在r陣列中，從r[0]到r[n-1]，長度為n，且最大值小於m。為了函式操作的方便，約定除r[n-1]外所有的r[i]都大於0，r[n-1]=0。函式結束後，結果放在sa陣列中，從sa[0]到sa[n-1]。

　　函式的第一步，要對長度為1的字串進行排序。一般來說，在字串的題目中，r的最大值不會很大，所以這裡使用了基數排序。如果r的最大值很大，那麼把這段程式碼改成快速排序。程式碼：

for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;

　　這裡x陣列儲存的值相當於是rank值。下面的操作只是用x陣列來比較字元的大小，所以沒有必要求出當前真實的rank值。

　　接下來進行若干次基數排序，在實現的時候，這裡有一個小優化。基數排序要分兩次，第一次是對第二關鍵字排序，第二次是對第一關鍵字排序。對第二關鍵字排序的結果實際上可以利用上一次求得的sa直接算出，沒有必要再算一次。程式碼：

for(p=0,i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;

　　其中變數j是當前字串的長度，陣列y儲存的是對第二關鍵字排序的結果。然後要對第一關鍵字進行排序，程式碼：

for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];

　　這樣便求出了新的sa值。在求出sa後，下一步是計算rank值。這裡要注意的是，可能有多個字串的rank值是相同的，所以必須比較兩個字串是否完全相同，y陣列的值已經沒有必要儲存，為了節省空間，這裡用y陣列儲存rank值。這裡又有一個小優化，將x和y定義為指標型別，複製整個陣列的操作可以用交換指標的值代替，不必將陣列中值一個一個的複製。程式碼：

for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;

　　其中cmp函式的程式碼是：

int cmp(int *r,int a,int b,int l)
{return r[a]==r[b]&&r[a+l]==r[b+l];}

　　這裡可以看到規定r[n-1]=0的好處，如果r[a]=r[b]，說明以r[a]或r[b]開頭的長度為l的字串肯定不包括字元r[n-1]，所以呼叫變數r[a+l]和r[b+l]不會導致陣列下標越界，這樣就不需要做特殊判斷。執行完上面的程式碼後，rank值儲存在x陣列中，而變數p的結果實際上就是不同的字串的個數。這裡可以加一個小優化，如果p等於n，那麼函式可以結束。因為在當前長度的字串中，已經沒有相同的字串，接下來的排序不會改變rank值。例如圖1中的第四次排序，實際上是沒有必要的。對上面的兩段程式碼，迴圈的初始賦值和終止條件可以這樣寫：

for(j=1,p=1;p<n;j*=2,m=p) {…………}

　　在第一次排序以後，rank陣列中的最大值小於p，所以讓m=p。

　　整個倍增演算法基本寫好，程式碼大約25行。

　　演算法分析：倍增演算法的時間複雜度比較容易分析。每次基數排序的時間複雜度為O(n)，排序的次數決定於最長公共子串的長度，最壞情況下，排序次數為logn次，所以總的時間複雜度為O(nlogn)。