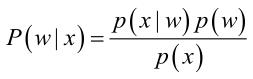貝葉斯啊貝葉斯,你這腦袋咋長的
以前不懂貝葉斯,怎麼看都困,考試過了就再也想不起來了,如今工作才發現這些數學知識如此有用,而且那麼神祕又充滿智慧,但是理解了之後,發現原來這麼簡單,之後不由的感嘆,簡單中的智慧太他麼神奇了!
學習SLAM遇到了卡爾曼濾波,學習卡爾曼濾波遇到了貝葉斯,於是隨便找了一篇部落格啃起來,發現這個例子之前很久就看過,現在再看,真有意思:

再看貝葉斯公式:
變換一下:
來來來,理解一下來:
我們從公園中抓了一個人,是個男的,還穿著涼鞋的,這個概率是多少???好,給你一個智慧機器人去抓,具體過程如下:
設: p(w1):抓到一個男人的概率;
p(x):抓到一個穿涼鞋的概率;
那麼:我們開始抓人了:
情況一:抓到一個“人”,我們一看:
機器人 : 我擦,男的!
你 :概率多少?
機器人 :p(w1);
你 : OK!再看看穿涼鞋了嗎?
機器人 :嗯嗯,穿啦!
你 :好,這個男的穿拖鞋的概率是多少?
機器人 :奧!已知是的男的哈,P(x|w1)啊。
你 :行了,把者兩個概率給我乘一塊兒!
機器人 :嗷!倆概率不相關哈!p(w1)P(x|w1)哦了,完事!
情況二:抓到一個“人”,我們一看:
機器人: 我擦,穿涼鞋啦!
你 :概率多少?
機器人 :p(x);
你 : OK!再看看是男的還是女的?
機器人 :嗯嗯,男噠!
你 :好,這個穿涼鞋的人是男人的概率多少?
機器人 :噢,已知是個穿涼鞋的,P(w1|x)啊。
你 :行了,把者兩個概率給我乘一塊兒!
機器人:嗷!倆概率不相關哈!p(x)P(w1|x)哦了,完事!
那麼問題來了:
兩種情況下,抓的都是同一類人(男的穿涼鞋),那麼概率是相等的,也就是說:
p(w1|x)p(x) = p(x|w1)p(w1)
沒有問題吧,你要非說有問題,那麼,我問問你,難道你先觀察“性別”還是先觀察“穿著”會影響你抓到這個人的概率嗎?注意哈,已經抓住了,取樣過程已經結束了,跟你先觀察“性別”還是“穿著”沒關係啦!OK!
總結一下:
生活中很多性質都是同時存在於同一個個體或者事件當中的,很多個體同時具備很多不相關的性質的時候,我們很難一下子弄清他們之間的關係,就例如上面的例子,而我們研究這種問題的時候,習慣性的一個性質一個性質的進行研究,必如研究(統計)性別比例時,不考慮其他因素,統計穿著時,不考慮性別,這樣就很容易的獲得了各個性質的獨立分佈情況,注意,由於我們是獨立統計的,所以獲取的統計結果也是獨立的,然而,當我們需要對幾種性質同時存在的“事實”進行研究時,研究的問題發生了變化,問題不再是“男-女”“穿拖鞋-沒穿拖鞋”兩個問題的獨立思考過程了,變成了“男-拖鞋”“男-沒穿拖鞋”“女-穿拖鞋”“女-沒穿拖鞋”這樣一個問題了,兩個統計問題變成了一個,實際上我們可以通過統計來對問題進行分析,比如統計以下情況的概率問題:
男穿拖鞋---P1
男沒穿拖鞋-----P2
女穿拖鞋----P3
女沒穿拖鞋-----P4
.......................................................................................................................................................................................................