3、複習線性代數知識
矩陣(向量是隻有一行或者一列的矩陣)
m行n列的矩陣簡稱m x n矩陣,記為:

行向量B和列向量A

矩陣加法(同型矩陣才能相加)
矩陣A和B都是m x n矩陣:
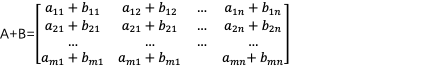
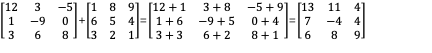
矩陣加法運算規律
- A + B = B + A
- (A + B) + C = A + (B + C)
矩陣乘法
數k與m x n型矩陣相乘:等於k與矩陣的每一個元素單獨相乘

矩陣數乘的運算規律
- 1A = A
- x(yA) = (xy)A
- k(A + B) = kA + kB
- (x + y)A = xA + yA
相關推薦
3、複習線性代數知識
矩陣(向量是隻有一行或者一列的矩陣) m行n列的矩陣簡稱m x n矩陣,記為: 行向量B和列向量A 矩陣加法(同型矩陣才能相加) 矩陣A和B都是m x n矩陣: 矩陣加法運算規律 A + B = B + A (A + B) + C = A + (B + C
機器學習筆記(3):線性代數回顧
目錄 1)Matrices and vectors 2)Addition and scalar multiplication 3)Matrix-vector multiplication 4)Matrix-matrix multiplication 5)Matrix multip
機器學習中的線性代數知識(下)
關於作者 作者小碩一枚,研究方向為機器學習與自然語言處理,歡迎大家關注我的個人部落格https://wangjie-users.github.io/,相互交流,一起學習成長。 前言 在機器學習中的線性代數知識(上)一文中,主要講解了矩陣的本質,以及對映視角下的特
線性代數知識彙總
1. 線性代數知識圖譜 線性代數是代數學的一個分支,主要處理線性關係問題。線性關係意即數學物件之間的關係是以一次形式來表達的。例如,在解析幾何裡,平面上直線的方程是二元一次方程;空間平面的方程是三元一次方程,而空間直線視為兩個平面相交,由兩個三元一次方程所組成的方程組來表
Unity學習(三)Unity Shader入門(基礎知識篇)+線性代數複習(未完待續)
至於為什麼剛建立了指令碼,現在就要做Shader了。。說多了都是淚 1.建立一個新的材質 Material Assert -> Create -> Material 拖到Scene中的某個物體上 2.建立一個新的Shader Assert -> Create -
深度學習概率知識、線性代數、機器學習、深度學習、計算機視覺等熱點問題
深度學習500問,以問答形式對常用的概率知識、線性代數、機器學習、深度學習、計算機視覺等熱點問題進行闡述,以幫助自己及有需要的讀者。 全書分為15個章節,近20萬字 第一章 數學基礎 1 1.1標量、向量、張量之間的聯絡 1 1.2張量與矩陣的區別? 1 1.3矩陣和向
[線性代數] 3.矩陣乘法的幾種求法
com 就是 法則 es2017 img 向量 矩陣 技術分享 組合 已知矩陣A和矩陣B,求A和B的乘積C=AB 矩陣A大小為mxn,矩陣B大小為nxp。 常規方法 矩陣C中每一個元素Cij = A的第i行 乘以(點乘) B的第j列 列方法 矩陣C的第i列 = 矩
數學-線性代數-#6 線性代數-#6 向量空間、列空間、R^n與子空間
都是 中間 探索 數量 就是 相同 三維 核心 三元 線性代數-#6 向量空間、列空間、Rn與子空間 讓我們回想一下#1的內容,當我們在用向量的新視角看待線性方程組時,曾經提到以“向量的圖像”作為代數學與幾何學橋梁的想法。 而現在,讓我們沿著這個想法深入探索下去,將其作
程序員的數學 3 線性代數pdf
對稱 字母 合成 12px pos com 定性 基於 角度 下載地址:網盤下載 內容簡介 · · · · · ·本書沿襲“程序員的數學”系列平易近人的風格,用通俗的語言和具象的圖表深入講解了編程中所需的線性代數知識。內容包括向量、矩陣、行列式、秩、逆矩陣、線性方程、L
數學-線性代數導論-#9 Ax=b的解:存在性、解法、解的數量、解的結構
運算 結構 要求 方法 一個 問題 -s 通過 概念 線性代數導論-#9 Ax=b的解:存在性、解法、解的結構、解的數量 終於,我們在b為參數的一般情況下,開始分析Ax=b的解,包括標題中的四個方面。 首先是解的存在性。 從幾何上說,當且僅當向量b位於列空間C(A)內時
數學-線性代數導論-#11 基於矩陣A生成的空間:列空間、行空間、零空間、左零空間
strong pos div 直接 jpg 不能 多次 常見 變化 線性代數導論-#11 基於矩陣A生成的空間:列空間、行空間、零空間、左零空間 本節課介紹和進一步總結了如何求出基於一個m*n矩陣A生成的四種常見空間的維數和基: 列空間C(A),dim C(A) =
數學 - 線性代數 - #12 向量空間的衍生:矩陣空間、微分方程的解、圖
對象 矩陣 mar nodes all 向量 cnblogs 導論 概念 線性代數導論-#12 向量空間的衍生:矩陣空間、微分方程的解、圖 凡是可以進行加法和數乘運算的對象,我們都可以將其視為向量。 凡是對加法和數乘封閉的集合,我們都可以將其視為空間。 分析空間時,我們著
線性代數基礎知識(二)——運算和性質【轉載】
這樣的 寫作 9.png 改變 通過 內容 你會 列空間 根據 3 運算和性質 在這一節中,我們將介紹幾種矩陣/向量的運算和性質。很希望這些內容可以幫助你回顧以前知識,這些筆記僅僅是作為上述問題的一個參考。 3.1 單位矩陣與對角矩陣 單位矩陣,記作I ∈ Rn×n,
線性代數矩陣知識
補充一些數學知識: 首先AB相似:P-1*A*P=B, AB合同:CT*A*C=B, 二次型:係數在K中的一個n元二次多項式。由其生成的矩陣稱為二次型的矩陣,二次型的矩陣一定是對稱矩陣! 正定矩陣:實二次型xT*A*x > 0, x為列向量。 性質:假設A為正定矩陣 1
形象理解線性代數(三)——列空間、零空間(核)、值域、特徵值(特徵向量)、矩陣與空間變換、矩陣的秩
這裡,我們還是要以 形象理解線性代數(一)——什麼是線性變換?為基礎。矩陣對向量的作用,可以理解為線性變換,同時也可以理解為空間的變換,即(m*n)的矩陣會把一個向量從m維空間變換到n維空間。 一、矩陣的列空間與矩陣的秩以及值域的關係 矩陣的列空間,其實就是矩陣的列所組成的空間。比如我們考慮
線性代數之——線性相關性、基和維數
1. 線性相關性 矩陣 A A A 的列是線性不相關的當且僅當
線性代數之——克拉默法則、逆矩陣和體積
1. 克拉默法則 這部分我們通過代數方法來求解 \(Ax=b\)。 用 \(x\) 替換單位矩陣的第一列,然後再乘以 \(A\),我們得到一個第一列為 \(b\) 的矩陣,而其餘列則是從矩陣 \(A\) 中對應列直接拷貝過來的。 利用行列式的乘法法則,我們有 \[|A|(x_1)=|B_1|\]
【線性代數】3-4:方程組的完整解( $Ax=b$ )
title: 【線性代數】3-4:方程組的完整解( Ax=bAx=bAx=b ) categories: Mathematic Linear Algebra keywords: Ax=b Special Solution Full Column Rank F
矩陣乘法和逆矩陣-線性代數課時3(MIT Linear Algebra , Gilbert Strang)
這是Strang教授的第三講,講解的內容是矩陣乘法和矩陣的逆。矩陣乘法在前面已經使用過,本節課教授只是集中細緻的講解矩陣乘法滿足的定律和幾種計算矩陣乘法的方法,矩陣的逆是本節課的重要內容。 矩陣乘法 首先介紹矩陣運算的條件和滿足的運算規律,
3、CAN詳解--基礎知識
基礎知識 一、背景 二、發展 三、匯流排優點 四、匯流排要點 1、CAN的應用 (1)車載網路構想 (2)應用例項 (3)連線圖 2、CAN協議基本概念

