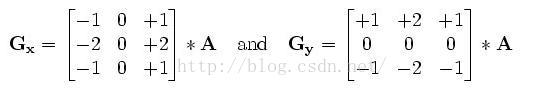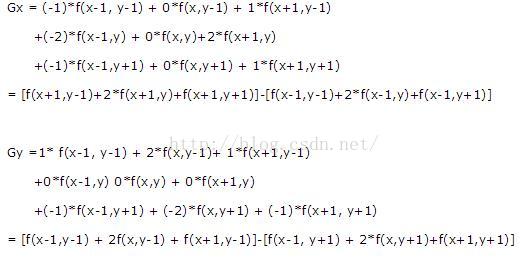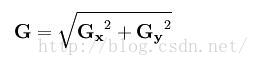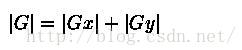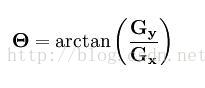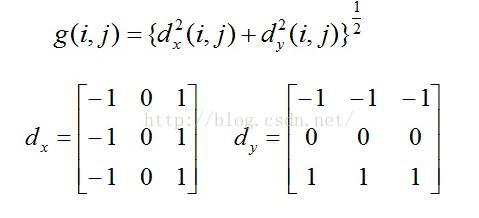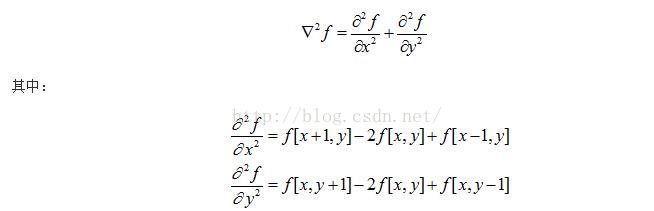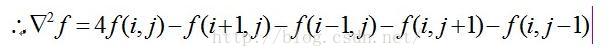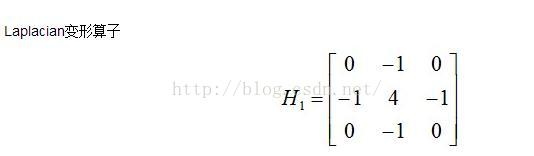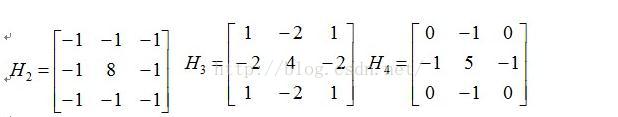1.Sobel邊緣檢測演算法

sobel邊緣運算元認不同為鄰域的畫素對當前畫素產生的影響不是等價的，所以距離不同的畫素具有不同的權值，對運算元結果產生的影響也不同。一般來說，距離越大，產生的影響越小。這兩個卷積因子分別對垂直邊緣和水平邊緣影響最大，兩個卷積的最大值做為該點的輸出位。

該運算元包含兩組3*3的矩陣，分別為影象橫向及縱向，將之與影象作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以A代表原始影象，Gx及Gy分別代表經橫向及縱向邊緣檢測的影象灰度值，其公式如下：

具體計算如下：

其中f(a,b)表示影象(a,b)點的灰度值；

影象的每一個畫素的橫向及縱向灰度值通過以下公式結合，來計算該點灰度的大小：

通常，為了提高效率，使用不開平方的近似值：

如果梯度G大於某一閾值，則認為改點(x,y)為邊緣點。

然後可用以下公式計算梯度方向：

sobel運算元根據畫素點上下、左右鄰點灰度加權差，在邊緣處達到極值這一現象檢測邊緣。對噪聲具有平滑作用，提供較為精確的邊緣方向資訊，邊緣定位精度不夠高。當對精度要求不是很高時，是一種較為常見的邊緣檢測方法。

程式碼：

void Sobel(unsigned char *pSource, unsigned char *pDst)
{
	int				i,j,Gx,Gy,nSum;
	unsigned char	*pDs1,*pDs2,*pDs3,*pDs4,*pDst5,*pDst6,*pDst7,*pDst8,*pDst9,*pResut;
	memset(pDst,0,sizeof(unsigned char)*m_nWidth*m_nHeight);
	pDs1 = pSource;
	pDs2 = pDs1+1;
	pDs3 = pDs2+1;
	pDs4 = pSource+m_nWidth;
	pDst5 = pDs4+1;
	pDst6 = pDst5+1;
	pDst7 = pSource+2*m_nWidth;
	pDst8 = pDst7+1;
	pDst9 = pDst8+1;
	pResut = pDst+m_nWidth+1;

	for (i=1;i<m_nHeight-1;i++)
	{
		for (j=1;j<m_nWidth-1;j++)
		{
			Gx = (*pDs3)+2*(*pDst6)+(*pDst9)
				-(*pDst7)-(*pDs1)-2*(*pDs4);
			Gy = (*pDs1)+2*(*pDs2)+(*pDs3)
				-(*pDst7)-2*(*pDst8)-(*pDst9);
			nSum = abs(Gx)+abs(Gy);
			*pResut = nSum>175?255:0;
			pDs1++;
			pDs2++;
			pDs3++;
			pDs4++;
			pDst5++;
			pDst6++;
			pDst7++;
			pDst8++;
			pDst9++;
			pResut++;
		}
		pDs1+=2;
		pDs2+=2;
		pDs3+=2;
		pDs4+=2;
		pDst5+=2;
		pDst6+=2;
		pDst7+=2;
		pDst8+=2;
		pDst9+=2;
		pResut+=2;
	}
}
 

2.Robert運算元——無方向一階銳化

3.Priwitt運算元——無方向一階銳化

Priwitt運算元在一個方向求微分，而在另一個方向求平均，因而對噪聲相對不敏感，有抑制噪聲的作用，但是畫素平均相對於對影象的低通濾，所以Prewitt運算元對邊緣的定位不如Roberts運算元。與Sobel相比，有一定的抗干擾性，影象效果比較乾淨。

幾種方法的效果比較：

• Sobel運算元與Priwitt演算法的思路相同，屬於同一型別，因此處理效果基本相同；
• Roberts運算元的模板時2*2，提取資訊弱；
• 單方向銳化經過處理之後，也可以對邊界進行增強。

4.拉普拉斯運算元

二維函式f(x,y)的拉普拉斯是一個二階的微分，定義為：

最終結果為：

Laplacian運算元利用二階導數資訊，具有各向同性，即與座標軸方向無關，座標軸旋轉後梯度結果不變。使得影象經過二階微分後，在邊緣處產生一個陡峭的零交叉點，根據這個對零交叉點判斷邊緣。

為了改善銳化效果，可以脫離微分的計算原理，在原有的運算元基礎上，對模板係數進行改變，獲得Laplacian變形運算元

Laplacian運算元對噪聲比較敏感，Laplacian運算元有一個缺點是它對影象中的某些邊緣產生雙重響應。所以影象一般先經過平滑處理，通常把Laplacian運算元和平滑運算元結合起來生成一個新的模板。