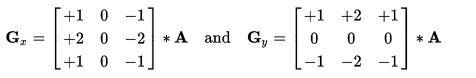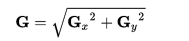完成時間：2017/1/23 

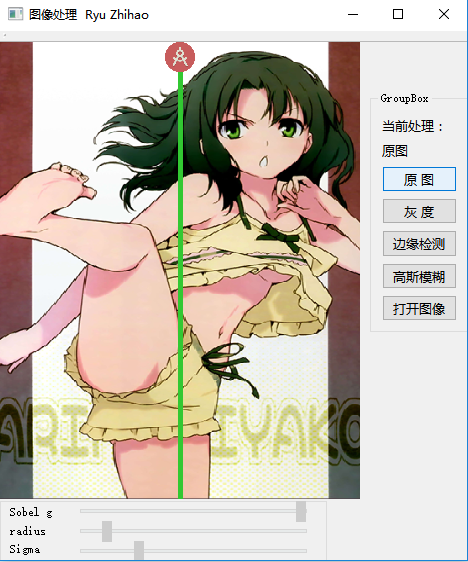
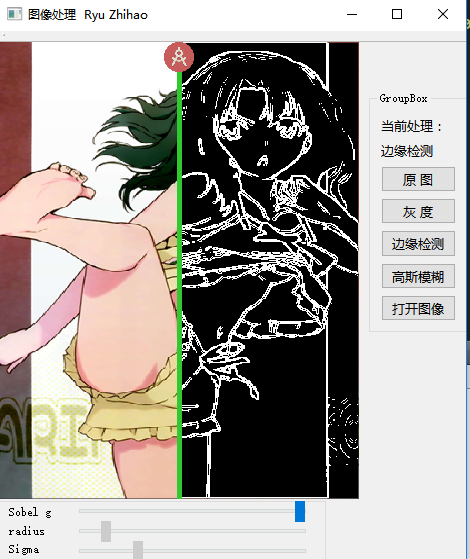
我的實現結果如下：（圖一為原圖，圖二為邊緣檢測結果）

關於Sobel運算元（英文部分來源於Wikipedia）

         The Sobel operator, sometimes called the Sobel–Feldman operator or Sobel filter, is used inimage processing and computer vision, particularly within edge detection algorithms where it creates an image emphasising edges. It is named after 

Sobel運算元，也被稱為Sobel-Feldman運算元，或者Sobel濾波，是在影象處理和計算機視覺得到廣泛應用的一種影象邊緣檢測演算法。它由斯坦福大學人工智慧實驗室（SAIL）的Irwin Sobel和Gray Feldman而得名（在此膜拜數學大神！）。

     The operator uses two 3×3 kernels which are convolved with the original image to calculate approximations of the 

 Sobel運算元使用兩個（3x3）矩陣來對原圖進行卷積運算以計算出兩個方向的灰度差分（偏導）的估計值（一個水平方向、一個豎直方向）。我們假定A是原始影象（彩色影象需先轉換為灰度影象

    對應的計算過程如下：

       Gx = [ f(x+1,y-1)+2*f(x+1,y)+f(x+1,y+1)] - [f(x-1,y-1)+2*f(x-1,y)+f(x-1,y+1) ]
       Gy = [ f(x-1,y-1) + 2f(x,y-1) + f(x+1,y-1)] - [f(x-1, y+1) + 2*f(x,y+1)+f(x+1,y+1) 

上式中，f(x,y)為影象A中(x,y)處的灰度值。由此便可以計算出每個點的Gx和Gy。

At each point in the image, the resulting gradient approximations can be combined to give the gradient magnitude, using:

對於影象中的每個點，其梯度的估計值G便可以通過兩個方向的梯度Gx和Gy藉由下式得出：

   此時，我們只需要設定一個閾值Gmax（比如說：100，一般來講0-255左右為宜），若梯度G大於閾值Gmax，則可認為該點是一個邊界點。

   Using this information, we can also calculate the gradient's direction:

   當然，我們甚至可以通過Gx和Gy求得邊界點梯度變化的方向，只需應用下式即可。