文章目錄

• 聯合概率及其分佈、邊緣概率及其分佈、條件概率及其分佈
• 聯合概率與聯合概率分佈
• 邊緣概率與邊緣概率分佈
• 條件概率與條件概率分佈
• 聯合概率、邊緣概率、條件概率之間的關係
• 離散型分佈的情況
• 連續型分佈的情況
• 貝葉斯定理(貝葉斯公式)
• 先驗概率
• 後驗概率
• 貝葉斯公式

聯合概率及其分佈、邊緣概率及其分佈、條件概率及其分佈

聯合概率與聯合概率分佈

假設有隨機變數X與Y, 此時，P(X=a,Y=b)用於表示X=a且Y=b的概率。這類包含多個條件且所有條件同時成立的概率稱為聯合概率。聯合概率並不是其中某個條件的成立概率， 而是所有條件同時成立的概率。

聯合概率的一覽表稱為聯合分佈。

邊緣概率與邊緣概率分佈

P(X=a)或P(Y=b)這類僅與單個隨機變數有關的概率稱為邊緣概率。

邊緣概率的一覽表稱為邊緣分佈。

條件概率與條件概率分佈

在條件Y=b成立的情況下，X=a的概率，記作P(X=a|Y=b)或P(a|b)。

若只有兩類事件X和Y，那麼有

$\mathrm{P}(X=$

條件概率的分佈簡稱條件分佈，即已知兩個相關的隨機變數X和Y，隨機變數Y在條件{X=x}下的條件概率分佈是指當已知X的取值為某個特定值x之時，Y的概率分佈。

舉例：

撲克牌的花色及X、Y的聯合分佈如下所示。

下面我們來計算條件概率。上面的圖可以進一步表示為：

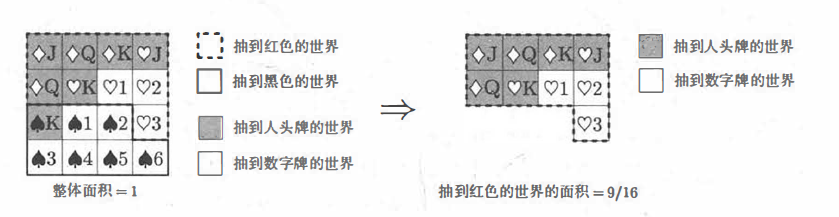
首先我們要知道：

P(Y=數字牌|X=紅色)+P(Y=人頭牌|X=紅色)=1

用公式可表示為：

$\sum _ { b } \mathrm { P } ( Y = b | X = a ) = 1$

由上圖，我們可以知道"X=紅色” 的世界中有三分之一的"Y=數字牌” ， 三分之二
的"Y=人頭牌” 。故我們就可以得到相應的條件概率公式：

P(Y=數字牌|X=紅色)=1/3

P(Y=人頭牌|X=紅色)=2/3

即在條件X=紅色成立時，Y=數宇牌的條件概率是1/3；在條件X=紅色成立時，Y=人頭牌的條件概率是2/3。

聯合概率、邊緣概率、條件概率之間的關係

“XY的聯合概率”=“X基於Y的條件概率”乘以“Y的邊緣概率” 。

離散型分佈的情況

離散型分佈下聯合概率、邊際概率、條件概率之間的等式關係：

$\operatorname { P } ( X = x ) = \sum _ { y } \operatorname { P } ( X = x , Y = y ) = \sum _ { y } \operatorname { P } ( X = x | Y = y ) \operatorname { P } ( Y = y )$

$\mathrm { P } ( X = x , Y = y )$為XY的聯合概率， $\mathrm { P } ( X = x )$為X的邊際概率， $\mathrm { P } ( X = x | Y = y )$ 為X基於Y的條件概率， $\mathrm { P } ( Y = y )$為Y的邊際概率。

連續型分佈的情況

$P _ { X } ( x ) = \int _ { y } P _ { X , Y } ( x , y ) \mathrm { d } y = \int _ { y } P _ { X | Y } ( x | y ) P _ { Y } ( y ) \mathrm { d } y$

只需要將“累加”換成“積分”，就是連續型分佈下聯合概率、邊際概率、條件概率之間的轉換計算公式。

貝葉斯定理(貝葉斯公式)

先驗概率

事件發生前的預判概率。可以是基於歷史資料的統計，可以由背景常識得出，也可以是人的主觀觀點給出。一般都是單獨事件概率，如P(X),P(Y)。

後驗概率

事件發生後求的反向條件概率；或者說，基於先驗概率求得的反向條件概率。概率形式與條件概率相同。

貝葉斯公式

設X和Y分別為兩類不同的事件，假設X和Y是互相獨立的(屬性條件獨立性假設)，由公式

$p ( X | Y) p ( Y ) = p ( X , Y ) = p ( Y | X ) p ( X )$

我們可以得到貝葉斯公式：

$p ( Y | X ) = \frac { p ( X | Y ) p ( Y ) } { p ( X ) }$

其中：

• P(Y|X)是後驗概率，一般是我們求解的目標。表示當擁有X這個條件後Y的概率，由於有X這個條件，後驗概率可能與先驗概率不同；

• P(X|Y)是條件概率，又叫似然概率，它表示在承認先驗的條件下另一個與之相關的隨機變數的表現，一般是通過歷史資料統計得到（即通過一個已知的小樣本統計得到）。

• P(Y) 是先驗概率，它表示我們對一個隨機變數概率最初的認識，一般都是人主觀給出的。貝葉斯中的先驗概率一般特指它。

• P(X)其實也是先驗概率，只是在貝葉斯公式中往往被認為是已知的，因此它一般被當做一個常量看待。使用樸素貝葉斯分類器計算時往往忽略這個P(X)，因為它是常量。

使用加法規則，則貝葉斯定理中的分母可以用出現在分子中的項表示：

$p ( X ) = \sum _ { Y } p ( X | Y ) p ( Y )$

我們可以把貝葉斯公式的分母p(x)看做歸一化常數，來確保貝葉斯公式左側的條件概率對於所有的Y的取值之和為1。