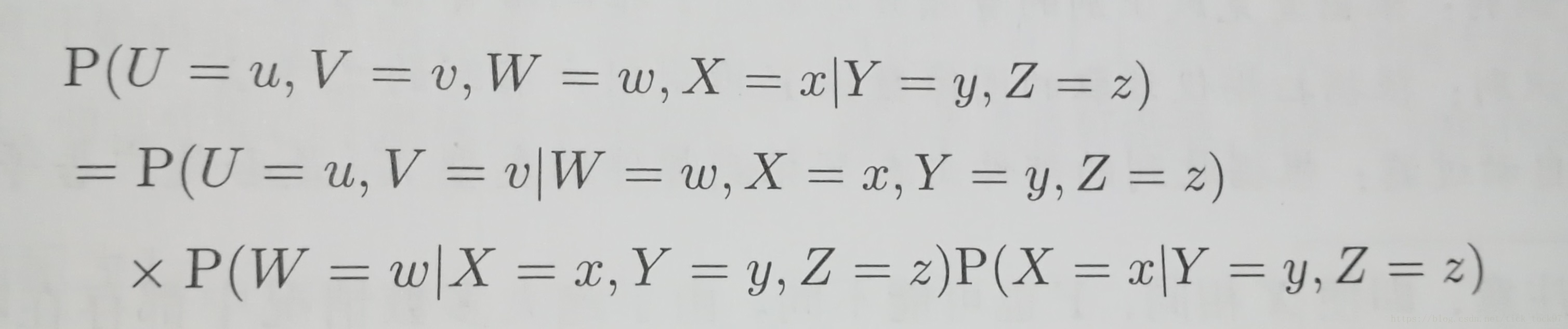2. 程式人生 > >聯合概率、邊緣概率、條件概率之間的關係&貝葉斯公式

聯合概率、邊緣概率、條件概率之間的關係&貝葉斯公式

阿新 • • 發佈：2019-02-20

前言

有挺長一段時間沒有更新部落格了，一方面是學校期末考試，後來又看了一些很基礎的程式設計數學思想的東西（《程式設計師的數學》第一卷），大多數東西都在之前的學習和使用中都有注意到，所以沒有什麼特別值得更新的。這次看到了卷2《程式設計師的數學2——概率統計》發現之前在概率論的學習過程中，忽略了一些比較重要的東西，這邊就來記錄一下，如果有寫的不對和寫得不好的地方，請各位看官老爺幫忙指出~

正文

這次主要介紹的是多個隨機變數之間的關係，主要涉及聯合概率，邊緣概率，條件概率這三種關係，還有一個利用他們之間關係匯出的非常重要的公式：貝葉斯公式

1.聯合概率

聯合概率指的是包含多個條件且所有條件同時成立

的概率，記作P(X=a,Y=b)或P(a,b)，有的書上也習慣記作P(ab)，但是這種記法個人不太習慣，所以下文采用以逗號分隔的記法。

一定要注意是所有條件同時成立！

2.邊緣概率

邊緣概率是與聯合概率對應的，P(X=a)或P(Y=b)，這類僅與單個隨機變數有關的概率稱為邊緣概率

3.聯合概率與邊緣概率的關係

P(X=a)=∑bP(X=a,Y=b)
P(Y=b)=∑aP(X=a,Y=b)

求和符號表示窮舉所有Y（或X）所能取得b（或a）後，所有對應值相加得到的和

4.條件概率

條件概率表示在條件Y=b成立的情況下，X=a的概率，記作P(X=a|Y=b)或P(a|b)，它具有如下性質：
“在條件Y=b下X的條件分佈”也是一種“X的概率分佈”，因此窮舉X的可取值之後，所有這些值對應的概率之和為1即：
∑aP(X=a|Y=b)=1

5.聯合概率、邊緣概率與條件概率之間的關係

P(X=a|Y=b)=P(X=a,Y=b)P(Y=b)

為了方便理解這個式子，可以將概率轉化為面積：

  • 聯合概率P(X=a,Y=b)
    滿足X=a且Y=b的面積
  • 邊緣概率P(X=a)
    不考慮Y的取值，所有滿足X=a的區域的總面積
  • 條件概率P(X=a|Y=b)
    在Y=b的前提下，滿足X=a的面積（比例）

示例1配圖

通過以上示例，稍加計算這三種概率之間的關係便可一目瞭然

6.條件聯合分佈的分解

我們可以根據具體情況，像下面這樣靈活的分解條件聯合分佈

P(X=a,Y=b|Z=c)=P(X=a|Y=b,Z=c)P(Y=b|Z=c)

這只是一個例子，作為啟發，類似的分解方法可以根據實際情況不同而進行不同的分解。為了大家可以有效掌握這種方法，建議自己從式子左側根據上面三種概率的關係式進行一遍推導。

再給大家留一個看起來非常複雜的式子，大家可以自己試試看能否從左側推導至右側
小挑戰

7.貝葉斯公式

說了那麼多，終於到大boss了，貝葉斯公式！但是，先別急，需要先引入兩個概念

  • 先驗概率：知道原因推結果的，P(原因)、P(結果|原因)等
  • 後驗概率：根據結果推原因的，P(原因|結果)等

貝葉斯公式解決的是一些原因X無法直接觀測、測量，而我們希望通過其結果Y來反推出原因X的問題，也就是知道一部分先驗概率，來求後驗概率的問題。

舉個栗子：

打到怪物就能獲得寶箱，但是寶箱有2/3的概率是陷阱，玩家可以通過魔法來檢查，但是有1/4的誤判概率，問：假設玩家利用魔法判定此寶箱沒有陷阱，求寶箱有陷阱的概率

我們已知的先驗概率有

P(有陷阱)=2/3；P(沒有發現|有陷阱)=1/4；P（發現了|沒有陷阱)=1/4

要求的後驗概率為

P(有陷阱|沒有發現)

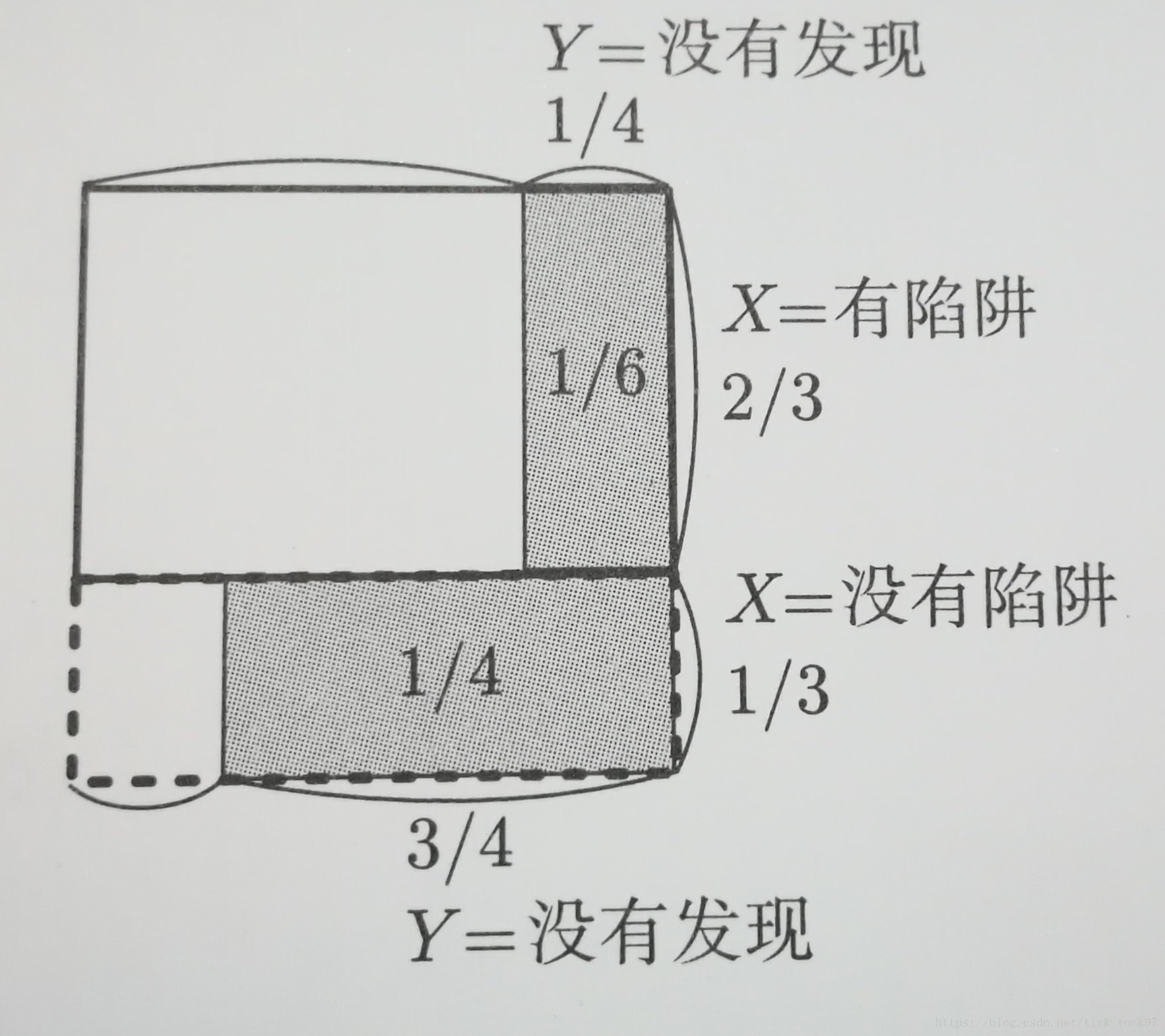
我們依舊使用面積來幫助我們解題，根據已知劃分出的面積情況如下圖所示
示例2配圖

我們可以推得：

P(有陷阱|沒有發現)=P(有陷阱,沒有發現)P(沒有發現)
P(沒有發現)=P(沒有發現|有陷阱)P(有陷阱)+P(沒有發現|沒有陷阱)P(沒有陷阱)

聯立兩式我們就可以得到一個由已知條件求P(有陷阱|沒有發現)的式子