B-樹

          是一種多路搜尋樹（並不是二叉的）：

     其中所有孩子節點個數的最大值稱為B-樹的階，通常用M表示。從查詢效率來說M>=3。一顆M階的B-樹或者是一顆空樹，或者是滿足一下要求的m叉樹。

    1）每個節點最多有m個分支（子樹）；而最少分支棵樹要看是否為根節點，根節點至少有2個分支，非根節點至少有[m/2]（向上取整）個分支。

    2) 有n個分支的節點有n-1個關鍵字，它們按照遞增順序排序。k=2(根節點)或者[m/2](非根節點)

                              其中，n，為關鍵字的個數，ki(1<=k<=n)為該節點的關鍵字且滿足ki<ki+1;pi(0<=i<=n)為該節點的孩子節點指標且滿足pi(1<=i<=n-1)所指節點上的關鍵字ki且小於ki+1，p0所指結點上的關鍵字小於k1，pn所指節點上的關鍵字大於kn.

    4)節點內各個關鍵字互不相等且按照從小到大排序。

    5)各個底層是葉子節點，它們處於同一層；葉子節點下面是失敗節點（可以是空指標表示），是查詢失敗到達的位置。

擴充套件：平衡m叉查詢樹是指每個關鍵字的左側子樹與右側子樹高度差的絕對值不能超過 1 的查詢樹，其節點結構與上面提到的B-樹結構相同。由此可見B-樹是平衡m叉查詢樹，但是限制更強，要求所有葉子節點都要在同一層。

   如下圖所示：

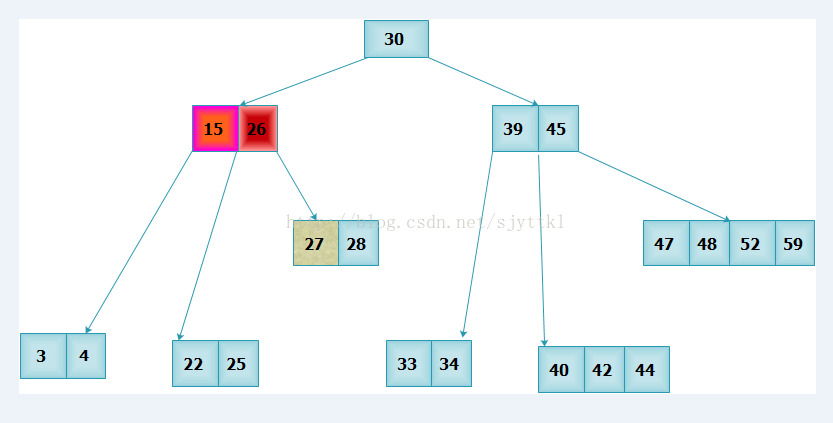
1，節點的分支數關鍵字增加1，最大分支數就是B-樹的階樹，因此m階的B-樹中節點最多有m個分支。通過下圖可以看出，圖中是一個5階B-樹（這裡的階就是樹的度）。

   2，下面是一顆5階B-樹，因此[m/5]=[m/2]=3，可以看出圖中除了根節點外，所有節點最少有三個分支。

   3，如果根節點沒有關鍵字就沒有分支，此時B-樹就是一個空樹，如果根結點有關鍵字，則其分支必大於或等於2，因為分支數等於關鍵字+1。

   4，右下圖可以知曉：除根節點外，節點中的關鍵字的個數至少為2，因為分支數至少為3，分支數比關鍵字數多1；還可以看出節點內關鍵字都是有序的，並且在同一層上，左邊節點內所有關鍵字均小於右邊節點內所有關鍵字。

   5，B-樹一個關鍵的特性是：下層節點內的關鍵字取值總是落在上層節點關鍵字所劃分的區間內，具體落在哪個區間，可以由它們的指標看出。

    B-樹的基本操作

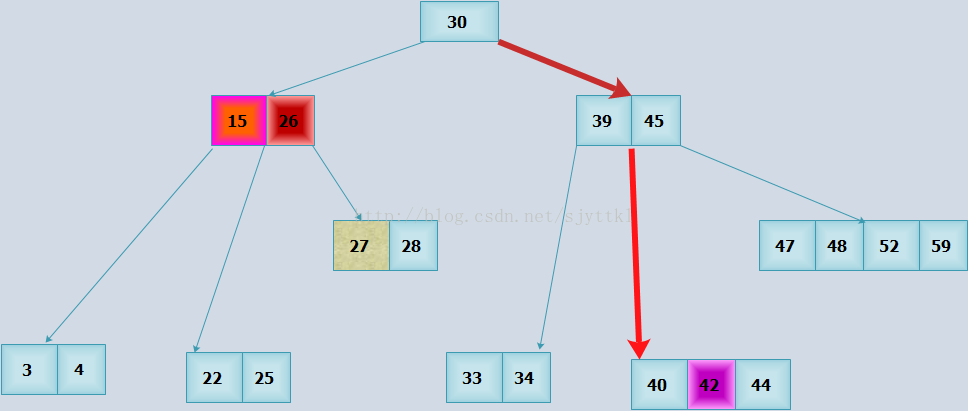
1，B-樹的查詢

B-樹很簡單，是二叉排序樹的擴充套件，二叉排序樹是二路查詢，B-樹是多路查詢，因為B-樹內關鍵字是有序的，在節點內進行查詢的時候除了順序查詢之外，還可以用這半查詢來提高效率。

                           例如，需要查詢關鍵字42。首先在根節點查詢，因為42>30，則沿著根節點p[1]往下走；在子樹根中查詢，因為39<42<45,則沿著子樹根節點中指標p[1]往下走，在下層節點中查詢關鍵字42成功，查詢結束。

                            如果下面的圖片看不見請點選這裡  

2，B-樹的插入和刪除

 B^-樹的生成也是從空樹起，逐個插入關鍵字而得。但由於B^-樹結點中的關鍵字個數必須≥ceil(m／2)-1，因此，每次插入一個關鍵字不是在樹中新增一個葉子結點，而是首先在最低層的某個非終端結點中新增一個關鍵字，若該結點的關鍵字個數不超過m-1，則插入完成，否則要產生結點的“分裂”，

如圖（a） 為3階的B^-樹(圖中略去F結點(即葉子結點))，假設需依次插入關鍵字30，26，85。

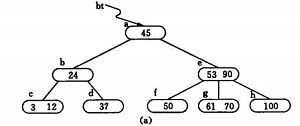
1) 首先通過查詢確定插入的位置。由根*a 起進行查詢，確定30應插入的在*d 節點中。由於*d 中關鍵字數目不超過2（即m-1），故第一個關鍵字插入完成：如（b）

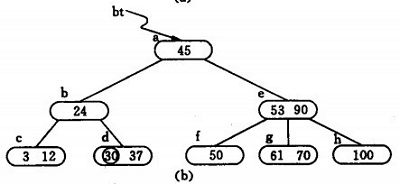
2) 同樣，通過查詢確定關鍵字26亦應插入 *d. 由於*d節點關鍵字數目超過2，此時需要將 *d分裂成兩個節點，關鍵字26及其前、後兩個指標仍保留在 *d 節點中，而關鍵字37 及其前、後兩個指標儲存到新的產生的節點 *d` 中。同時將關鍵字30 和指示節點 *d `的指標插入到其雙親的節點中。由於 *b節點中的關鍵字數目沒有超過2，則插入完成.如（c）(d)

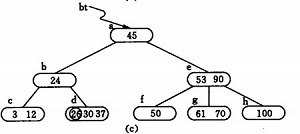
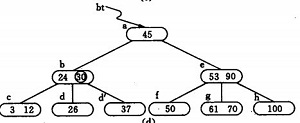
3) (e) -(g) 為插入85後;

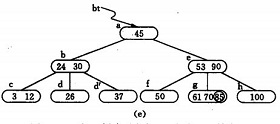
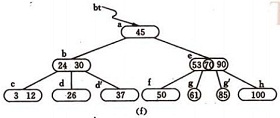
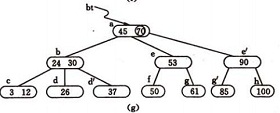
      反之，若在B^-樹上刪除一個關鍵字，則首先應找到該關鍵字所在結點，並從中刪除之，若該結點為最下層的非終端結點，且其中的關鍵字數目不少於ceil(m/2)，則刪除完成，否則要進行“合併”結點的操作。假若所刪關鍵字為非終端結點中的Ki，則可以指標Ai所指子樹中的最小關鍵字Y替代Ki，然後在相應的結點中刪去Y。例如，在下圖  圖4.1( a)的B^-樹上刪去45，可以*f結點中的50替代45，然後在*f結點中刪去50。

                                圖4.1( a)

因此，下面我們可以只需討論刪除最下層非終端結點中的關鍵字的情形。有下列三種可能：

    (1)被刪關鍵字所在結點中的關鍵字數目不小於ceil(m/2)，則只需從該結點中刪去該關鍵字Ki和相應指標Ai，樹的其它部分不變，例如，從圖  圖4.1( a)所示B^-樹中刪去關鍵字12，刪除後的B^-樹如圖  圖4.2( a)所示：

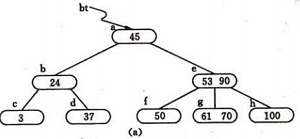
                           圖4.2( a)

   (2)被刪關鍵字所在結點中的關鍵字數目等於ceil(m/2)-1，而與該結點相鄰的右兄弟(或左兄弟)結點中的關鍵字數目大於ceil(m/2)-1，則需將其兄弟結點中的最小(或最大)的關鍵字上移至雙親結點中，而將雙親結點中小於(或大於)且緊靠該上移關鍵字的關鍵字下移至被刪關鍵字所在結點中。

[例如]，從圖圖4.2( a)中刪去50，需將其右兄弟結點中的61上移至*e結點中，而將*e結點中的53移至*f，從而使*f和*g中關鍵字數目均不小於ceil(m-1)-1，而雙親結點中的關鍵字數目不變，如圖圖4.2(b)所示。

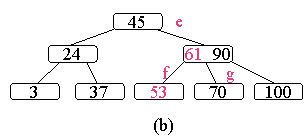
                               圖4.2(b)

       (3)被刪關鍵字所在結點和其相鄰的兄弟結點中的關鍵字數目均等於ceil(m/2)-1。假設該結點有右兄弟，且其右兄弟結點地址由雙親結點中的指標Ai所指，則在刪去關鍵字之後，它所在結點中剩餘的關鍵字和指標，加上雙親結點中的關鍵字Ki一起，合併到 Ai所指兄弟結點中(若沒有右兄弟，則合併至左兄弟結點中)。

[例如]，從圖4.2(b)所示 B^-樹中刪去53，則應刪去*f結點，並將*f中的剩餘資訊(指標“空”)和雙親*e結點中的 61一起合併到右兄弟結點*g中。刪除後的樹如圖4.2(c)所示。

                                圖4.2(c)

 如果因此使雙親結點中的關鍵字數目小於ceil(m/2)-1，則依次類推。

[例如]，在 圖4.2(c)的B-樹中刪去關鍵字37之後，雙親b結點中剩餘資訊(“指標c”)應和其雙親*a結點中關鍵字45一起合併至右兄弟結點*e中，刪除後的B^-樹如圖 4.2(d)所示。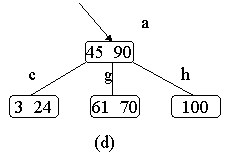  

B-樹主要應用在檔案系統

為了將大型資料庫檔案儲存在硬碟上以減少訪問硬碟次數為目的 在此提出了一種平衡多路查詢樹——B-樹結構 由其效能分析可知它的檢索效率是相當高的為了提高 B-樹效能’還有很多種B-樹的變型，力圖對B-樹進行改進