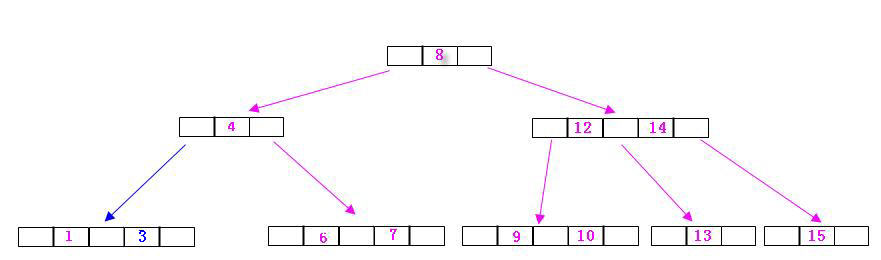
2-3樹所有葉子都在同一個層次,也就是說每一層的葉子數目都是相等的,如圖:

一:插入資料3,

插入的時候從根結點8發現,比8大往左走,到達4,發現比4小,繼續往左走,然後發現比1大,並且此時1結點只有一個結點,所以可以插入,如圖:

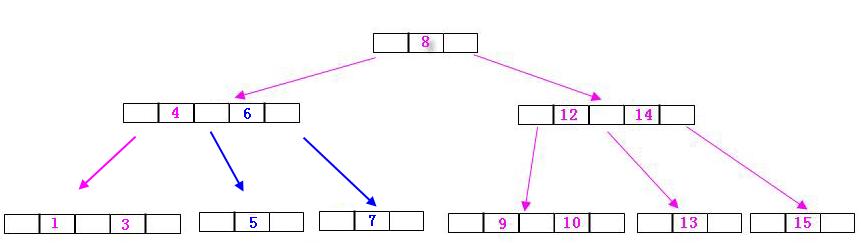
二.插入5

插入的時候從根結點8發現,比8大往左走,到達4,發現比4大,繼續往右走,而6,7結點此時是滿了無法插入,那麼就往上找4結點,4結點可以插入,此時插入的時候需要將6結點與4結點合併起來,也就是將6,7結點分裂,7成為6的右結點,5成為6的左節點(4的右結點),如圖:

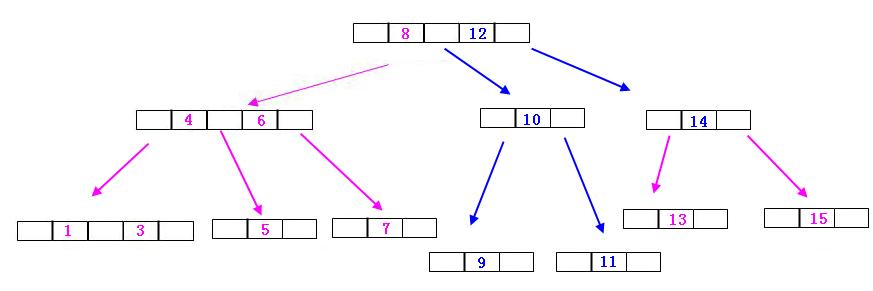
三.插入11

插入的時候,從根節點8比較,比8大往右走,在12,14結點中發現比12小,繼續往左走,找到了9,10,而此時9,10結點滿了,根據往上找原則,找12,14,而12,14也滿了,再繼續往上找原則,找到了8,此時8還有位置,8指向的12進行分裂得到12,14,8和12結合,12的右結點指向14,而剩餘的9,10,11組成10為根的結點,然後12的左結點連線10,如圖:

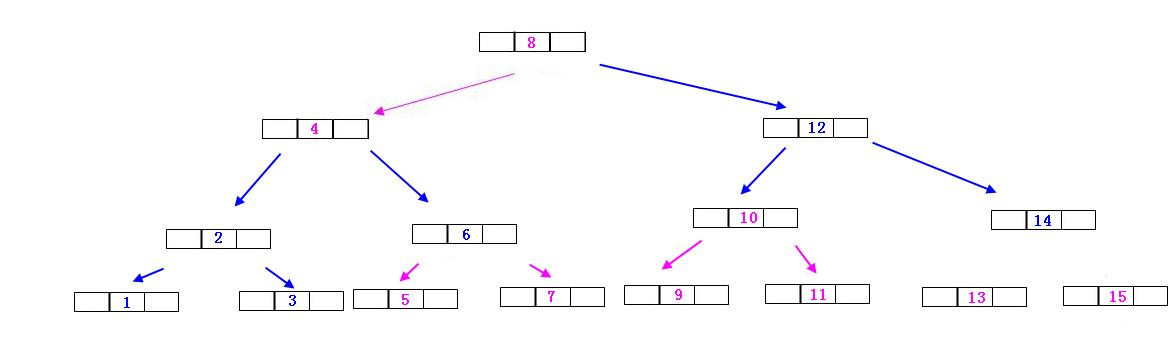
四.插入2

插入的時候,從根節點8比較,比8大往左走,比4大往左走,走到最後一個葉子結點1,3,發現此時滿了,無法插入,根據往上找的原則,找到4,6發現4,6結點也滿了,繼續往上找,8,12也滿了,由於根節點都滿了,所以就需要擴充套件樹的高度,這就是2-3樹的優勢了,充分利用樹高度達到查詢的時候可以更快地找到!

此時從底部開始分裂(1,3)結點,2成為1,3的父節點,如果此時4的左邊指向2則整棵樹的高度不符合2-3樹的定義,而此時發現右邊的高度有問題,所以進行(4,6)結點分裂,將4的右邊指向以6為5,7的父節點,此時以4為根節點的樹就達到了平衡的效果了,但是呢(8,12)為根節點的樹的左右高度不滿足,所以將(8,12)結點進行分裂,8的右邊指向12結點,(10,14以12為父節點),那麼就搞定了,如圖: