分類問題中，交叉熵函式是比較常用也是比較基礎的損失函式，原來就是了解，但一直搞不懂他是怎麼來的？為什麼交叉熵能夠表徵真實樣本標籤和預測概率之間的差值？趁著這次學習把這些概念系統學習了一下。

首先說起交叉熵，腦子裡就會出現這個東西： 

隨後我們腦子裡可能還會出現Sigmoid()這個函式:

pytorch中的CrossEntropyLoss()函式實際就是先把輸出結果進行sigmoid，隨後再放到傳統的交叉熵函式中，就會得到結果。

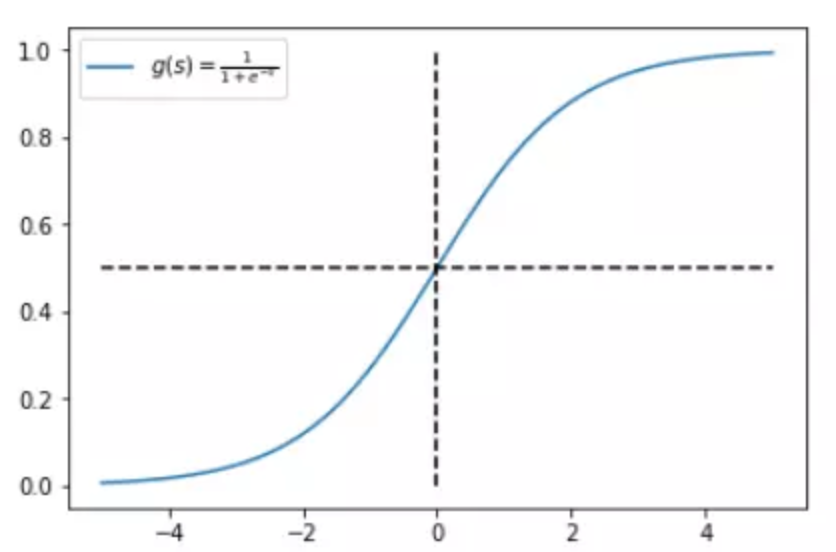
那我們就先從sigmoid開始說起，我們知道sigmoid的作用其實是把前一層的輸入對映到0~1這個區間上，可以認為上一層某個樣本的輸入資料越大，就代表這個樣本標籤屬於1的概率就越大，反之，上一層某樣本的輸入資料越小，這個樣本標籤屬於0的概率就越大，而且通過sigmoid函式的影象我們可以看出來，隨著輸入數值的增大，其對概率增大的作用效果是逐漸減弱的，反之同理，這就是非線性對映的一個好處，讓模型對處於中間範圍的輸入資料更敏感。下面是sigmoid函式圖：

既然經過sigmoid之後的資料能表示樣本所屬某個標籤的概率，那麼舉個例子，我們模型預測某個樣本標籤為1的概率是：

那麼自然的，這個樣本標籤不為1的概率是： 

從極大似然的角度來說就是：

上式可以理解為，某一個樣本x，我們通過模型預測出其屬於樣本標籤為y的概率，因為y是我們給的正確結果，所以我們當然希望上式越大越好。

下一步我們要在  P( y | x )  的外面套上一層log函式，相當於進行了一次非線性的對映。log函式是不會改變單調性的，所以我們也希望  log( P( y | x ) )  越大越好。

這樣，就得到了我們一開始說的交叉熵的形式了，但是等一等，好像還差一個符號。

因為一般來說我們相用上述公式做loss函式來使用，所以我們想要loss越小越好，這樣符合我們的直觀理解，所以我們只要  -log( P( y | x ) )  

上面是二分類問題的交叉熵，如果是有多分類，就對每個標籤類別下的可能概率分別求相應的負log對數然後求和就好了：

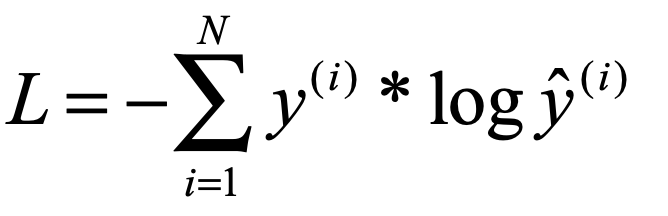
是不是突然也感覺有些理解了，(*^__^*) …… 

上面是對交叉熵進行了推到，下面要結合pytorch中的函式 CrossEntropyLoss()  來說一說具體怎麼使用了。

舉個小例子，假設我們有個一樣本，他經過我們的神經網路後會輸出一個5維的向量，分別代表這個樣本分別屬於這5種標籤的數值（注意此時我們的5個數求和還並不等於1，需要先經過softmax處理，下面會說），我們還會從資料集中得到該樣本的正確分類結果，下面我們要把經過神經網路的5維向量和正確的分類結果放到CrossEntropyLoss() 中，看看會發生什麼：

看一看我們的input和target： 　

可以看到我們的target就是一個只有一個數的陣列形式（不是向量，不是矩陣，只是一個簡單的陣列，而且裡面就一個數），input是一個5維的向量，但這，在計算交叉熵之前，我們需要先獲得下面交叉熵公式的。

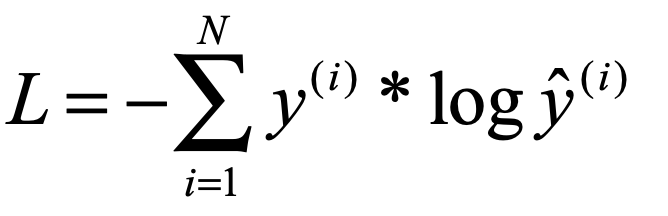
此處的需要我們將輸入的input向量進行softmax處理，softmax我就不多說了，應該比較簡單，也是一種對映，使得input變成對應屬於每個標籤的概率值，對每個input[i]進行如下處理：

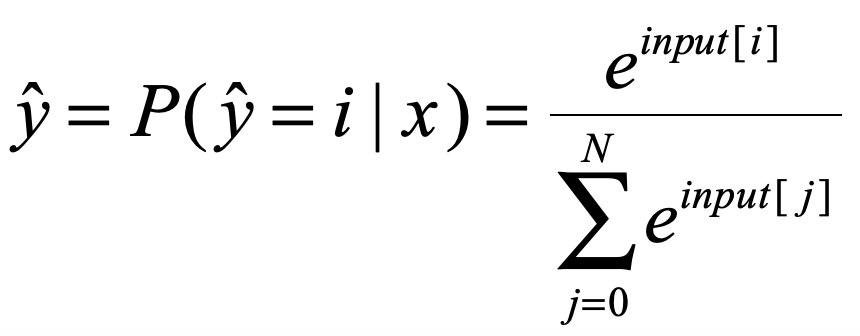
這樣我們就得到了交叉熵公式中的

隨後我們就可以把帶入公式了，下面我們還缺就可以了，而奇怪的是我們輸入的target是一個只有一個數的陣列啊，而是一個5維的向量，這什麼情況？

原來CrossEntropyLoss() 會把target變成ont-hot形式（網上別人說的，想等有時間去看看函式的原始碼隨後補充一下這裡），我們現在例子的樣本標籤是【4】（從0開始計算）。那麼轉換成one-hot編碼就是【0，0，0，0，1】，所以我們的最後也會變成一個5維的向量的向量，並且不是該樣本標籤的數值為0，這樣我們在計算交叉熵的時候只計算給定的那一項的sorce就好了，所以我們的公式最後變成了：

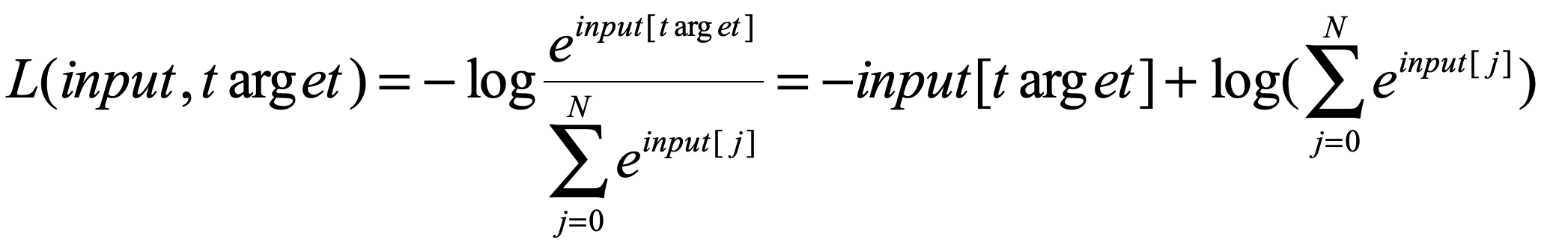
好，安裝上面我們的推導來執行一下程式：

破發科特~~~~~~

聖誕節快樂(*^__^*) ……