關於埃氏篩法詳解
那天的ppt講的不是很清楚 下來後好多同學都說沒聽懂(。。。。。)
我再補充一下
首先 關於原理

ppt上講的很清楚了 這個原理是相對簡單的 很好理解
如果原理你都理解了 那麼你直接去後邊看用法
如果 你還沒有理解 那麼 我再舉個例子
最樸素的判斷素數方法 是這樣的 對吧

那麼 現在我讓你判斷1-20 之內的素數 你會怎麼做
從1 遍歷到20 挨個判斷一下是不是素數 對吧
那麼我們來分析一下複雜度 如果不理解什麼是複雜度 你就認為我們算一下迴圈次數好了
從1-20 需要遍歷20次 對於每個數 極端情況下 需要sqrt(n)次才完成能判斷
這一共是多少次呢 sqrt(2)+sqrt(3)+sqrt(4)+sqrt(5)+.........sqrt(20) 次 對嗎
通過計算器 計算得到 答案是60 也就是需要60次
那麼我們再來看下 我們使用埃氏篩需要幾次
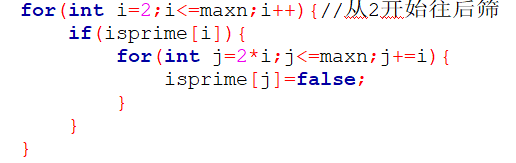
首先 外面的迴圈 毋庸置疑 從2-20遍歷 需要20次(其實是19 我們忽略 進為20)
我們來看裡面的操作
從2開始 2是素數 那麼4不是 6不是 8也不是 10、12、14、16、18、20 都不是 這是9次操作
然後3開始 6 9 12 15 18 都不是素數 這是5次操作
然後4 跳過 5 跳過 6 跳過
從7開始 14 不是素數 這是1次操作
後邊的 8 9 10 11 12 14 15 16 18 20 都會跳過
而11 13 17 19 都不會操作 因為他們的倍數 大於20了
那麼一共進行了20+9+5+1=35次操作 比那個60少了將近一半
其實因為我舉的例子很小 只到20 所以你看到的才快了這麼點
你可以想一下 如果數字變得很大的時候 比如一千萬 你用普通的篩法 是需要更多次數的
所以 這個埃氏篩法快的其實不止這麼一點--(至於究竟快多少 先不管了 你只要知道很快就好了)
下面說下 怎麼用它
明白了 原理 用起來就很靈活了
比如
問題一 求1-20之間的素數個數
int main(){
int cnt=0;//用來計數
bool isprime[21];
for(int i=0;i<=20;i++)isprime[i]=true;//先全部置為真
isprime[0]=isprime[1]=false;//1 0 不是素數
for(int i=2;i<=20;i++){//從2開始往後篩
if(isprime[i]){
for(int j=2*i;j<=20;j+=i){
isprime[j]=false;
}
}
if(isprime[i]){
cnt++;//如果是素數 就計數
}
}
printf("%d",cnt);
}問題二
就是ppt上的題目

#include<stdio.h>
#include<algorithm>
#include<math.h>
const int maxn=1e6+7;//總的範圍規定在這裡
using namespace std;
//我們將這個埃氏篩法寫成一個函式
bool isprime[maxn];
void sieve(){
for(int i=0;i<=maxn;i++)isprime[i]=true;
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn;i++){//從2開始往後篩
if(isprime[i]){
for(int j=2*i;j<=maxn;j+=i){
isprime[j]=false;
}
}
}
}
int l,r;
int main(){
//我們在程式剛開始 先呼叫這個函式
//把這個isprime陣列處理成我們想要的樣子 用來判斷素數
//這就是預處理的思想 我們在開頭處理這一次
//把isprime陣列 裡面 下標是素數的全部變成了true
//後邊想判斷是不是素數 直接用isprime[i]是不是真就好了
sieve();
int cnt=0;//計數
scanf("%d%d",&l&r);//輸入 l和r
for(int i=l;i<=r;i++){//遍歷 l到r 判斷就行了
if(isprime[i]){
cnt++;
}
}
printf("%d",cnt);
}
問題三 輸入一個數n 判斷他是不是素數(多組測試資料)
n的範圍是 (n<1e6)
這個題很有意思 題上說有多組測試資料(沒說幾組) 每次給你一個n
那麼其實意思就是說 有很多個n讓你判斷 他們是不是素數
而且n最大是1e6
那麼你們想一下
如果我第一個數給你1000000 你用普通的判斷素數的方法 需要sqrt(n)次才能判斷出來
也就是3000次才能判斷出來是不是素數 對吧
3000次也不多 那如果我輸入一共一萬組呢 就需要3000*10000次了吧
所以 這個時候 就體現了 預處理的重要性
我們先預處理出來 1e6以內的所有素數 這樣不管你輸入啥 我直接去看 是不是素數就好了
對吧
那麼 預處理 有些同學也想到了 但是他用最普通的篩法去做預處理
那麼你想一下 1e6每個你都需要去判斷一下是不是素數 我剛才在上邊算了 20以內的素數需要60次才能判斷出來
那1e6以內 需要多少次呢 我告訴你 大概需要1e9次(也就是十億次)
而用埃氏篩法需要幾次呢 可能你們現在還不會算 我直接告訴你們 需要70萬次
十億 和 七十萬 差別不用我說了吧 這就是這個演算法的效率 也是演算法的魅力所在。
#include<stdio.h>
#include<algorithm>
#include<math.h>
const int maxn=1e6+7;//總的範圍規定在這裡
using namespace std;
//我們將這個埃氏篩法寫成一個函式
bool isprime[maxn];
void sieve(){
for(int i=0;i<=maxn;i++)isprime[i]=true;
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn;i++){//從2開始往後篩
if(isprime[i]){
for(int j=2*i;j<=maxn;j+=i){
isprime[j]=false;
}
}
}
}
int n;
int main(){
sieve();//預處理
//輸入 n
while(scanf("%d",&n)!=EOF){
if(isprime[n]){
printf("Yes\n");
}
else{
printf("No\n");
}
}
}
