強化學習——基於策略梯度的強化學習演算法
在前面的章節裡,我們已經學習了基於值函式的強化學習演算法,他的核心思想是利用當前的策略 與環境進行互動,得到資料之後,利用得到的資訊來更新值函式,得到一個新的值函式之後,我們可以利用這個值函式產生一個新的策略 ,這個新的策略 比原來的策略有著更大的期望回報,以此迭代,最終我們將得到一個期望回報很高的策略。從這裡可以看出,基於值函式方法得強化學習演算法的核心是對值函式有一個好的評估,下面將介紹的基於策略梯度得強化學習演算法則是從另外一個角度考慮一個MDP的,他的想法會更加自然一些。
在開始介紹直接策略搜尋的強化學習演算法之前,我們有必要了解一下這種方法相比於我們之前介紹的基於值函式的方法的優缺點。
1. 直接策略搜尋是對策略進行引數化表示,與值函式相比,策略化引數的方法更簡單,更容易收斂。
2. 值函式的放法無法解決狀態空間過大或者不連續的情形
3. 直接策略的方法可以採取隨機策略,隨機策略可以將探索直接整合到演算法當中
當然值函式的方法也有一些優點:
1. 策略搜尋的方法更容易收斂區域性極值點
2. 在評估單個策略時,評估的並不好,方差容易過大
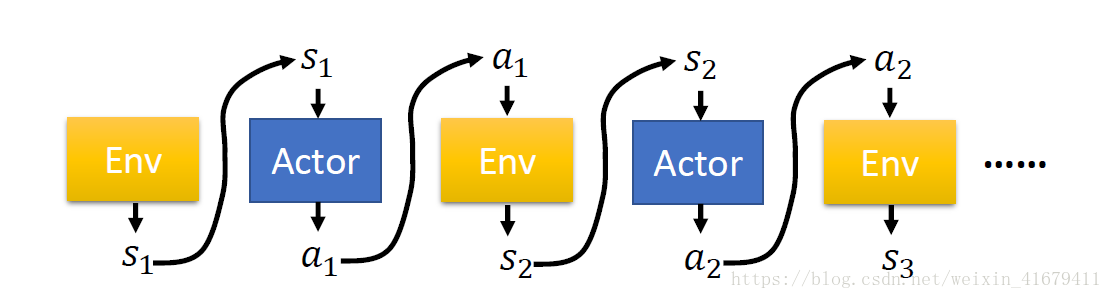
上圖是一個完整的MDP過程對於一個完整的取樣軌跡
我們有
這個式子中用到了馬氏性,認為一個狀態只與與之相鄰的前一個狀態有關。
其中 是策略的引數,一個策略完全由其引數決定。在實際應用中,這種關係是由神經網路刻畫的。
在定義了一條取樣軌跡的概率之後,我們來定義期望回報:
其中
過程如下圖所示,
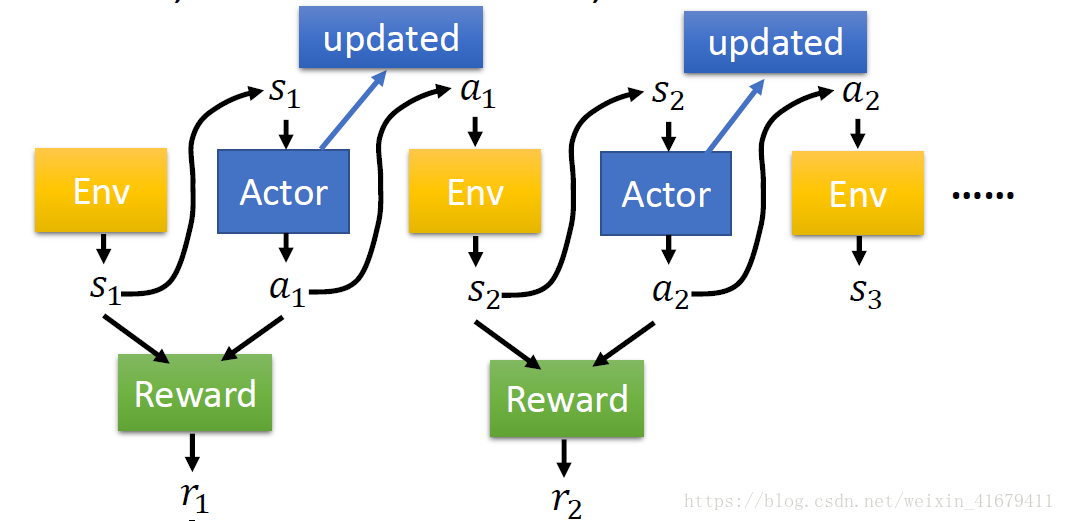
得到期望回報關於策略的表示式之後,我們的目標變得非常明確了,我們只需要優化這個函式,使之最大化即可。我們可以使用最常用的梯度下降的方法。
注意到:
