文章目錄

• 策略梯度網路結構
• 策略梯度網路權重的更新
• 策略梯度網路更新的時機
• 策略梯度動作的選擇
• 策略梯度概率更新幅度
• 最後

Q-learning與DQN都屬於基於值函式的深度強化學習，因為其輸出都是關於動作的值，然後再根據 $ϵ$

但是如果動作是一個連續性動作，他的值函式不可能完全計算出來，而策略梯度可以很好的解決動作連續性問題（我也還沒弄懂為什麼可以解決，想明白了再更新）

策略梯度網路結構

輸入結點為觀測到的特徵數與特徵值
隱藏層根據實際情況進行更改
輸出層為動作的數量，其值再經過softmax函式處理變為採取的概率值

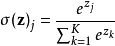
策略梯度網路權重的更新

神經網路都是根據誤差函式來進行更新，而從嚴格意義上來講，策略梯度演算法是沒有誤差的，因為其輸出只是選擇的概率值，為了進行權重更新，我們將選取的動作的概率乘以一個變數作為損失函式，而該變數的取值取決於該動作的獎勵收益
訓練目標為損失函式最大化，這樣就可以學習使獎勵收益越來越大，而選取該獎勵的概率也越來越大

策略梯度網路更新的時機

與基於值函式的深度強化學習演算法不同，基於值函式的演算法每一步都可以作為資料集進行學習，而策略梯度因為嚴格意義沒有誤差，所選取的誤差函式必須在一回合結束後才能獲得獎勵值。
故策略梯度只能在回合結束時更新策略梯度網路。而每一步的選擇都對網路有影響，故還需要用陣列將所出現的狀態，選取的動作，獲得的獎勵用陣列儲存起來，在回合結束時一併作為資料集經行網路更新

策略梯度動作的選擇

與 $\epsilon-greedy$貪婪策略不同，策略梯度輸出的是動作採取的概率，故直接根據該概率對動作進行選取即可

action = np.random.choice(range(prob_weights.shape[1]), p=prob_weights.ravel())

策略梯度概率更新幅度

程式碼如下：

discounted_ep_rs = np.zeros_like(self.ep_rs)
        running_add = 0
        for t in reversed(range(0, len(self.ep_rs))):
            running_add = running_add * self.gamma + self.ep_rs[t]
            discounted_ep_rs[t] = running_add

        # normalize episode rewards
        discounted_ep_rs -= np.mean(discounted_ep_rs)
        discounted_ep_rs /= np.std(discounted_ep_rs)
        return discounted_ep_rs

其中ep_rs代表每一步獲得獎勵，discounted_ep_rs代表每一步概率更新的幅度

最後

剛看完策略梯度，該演算法因為沒有采用 $\epsilon-greedy$故極其容易陷入最優解。給我的感覺該演算法有點像去除掉 $\epsilon-greedy$的DQN。若有表述不對的地方再進行更正。

如有錯誤，敬請指正
.