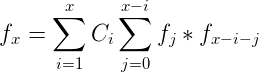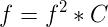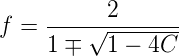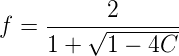CodeForces 438E The Child and Binary Tree(DP + 生成函式 + 多項式模運算)



大致題意:給定一個集合{Cn},一棵二叉樹上的所有節點的點權值從這個集合中選取。現在給定一個m,問對於1..m中的每一個數字i,權值和恰好為i的不同的二叉樹的個數有多少個。這裡形態不同但點權集合的二叉樹視為兩種方案。
與前面做的題目類似,這種題目我們還是用dp的思維去考慮。令fi表示權值和為i的二叉樹的個數。那麼考慮增加一個點x,這個點的權值可以取i,Ci表示數值i在初始給定集合中是否出現過,兩個兒子對應子樹的點權值和為fj和fk,那麼這樣的話就會對點權和為ci*(fj+fk)的方案數產生貢獻。於是我們可以寫出狀態轉移方程:
現在我們考慮這個式子。這是一個卷積套卷積的式子,直接去做的話是完成不了的。但是根據式子,我們表示成生成函式的形式,大致可以推出:
然後根據C[0]=0,f[0]=1,可以完善,得到:
我們需要求f,於是把f當作位置數,這個就是一個一元二次方程。可以解得這個方程的根是:
進行分子有理化得:
考慮到當取0的時候,f=1,C=0,如果取減號,那麼分母為0無意義,所有這裡只能取加號。
NTT加多項式開根再求逆元即可。具體見程式碼:
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod = 998244353;//(119 << 23) + 1;
const int modinv2 = (mod+1)/2; // 1/2 in F_p
const int G = 3;
const int N = 270010;
int c[N];
//取模加減乘
inline int add(int a,int b) {return a+b>=mod?a+b-mod:a+b;}
inline void inc(int&a,int b) {if ((a+=b)>=mod) a-=mod;}
inline int sub(int a,int b) {return a-b<0?a-b+mod:a-b;}
inline void dec(int&a,int b) {if ((a-=b)<0) a+=mod;}
inline int mul(int a,int b) {return (LL)a*b%mod;}
inline int qpow(int x,int n) {int ans=1;for (;n;n>>=1,x=(LL)x*x%mod) if (n&1) ans=(LL)ans*x%mod; return ans;}//quick power
//-------------------------------NTT--------------------------------
int wn[30],iwn[30]; //wn[i] = G^((P-1)/(2^i)) (mod P), iwn[i] = wn[i]^(-1) (mod P)
inline void init() //do this before NTT
{
wn[23] = qpow(G,(mod-1)/(1<<23));
for (int i=22;i>=0;i--) wn[i] = mul(wn[i+1],wn[i+1]);
iwn[23] = qpow(wn[23],(1<<23)-1);
for (int i=22;i>=0;i--) iwn[i] = mul(iwn[i+1],iwn[i+1]);
}
inline void revbin_permute(int a[],int n) {
int i=1, j=n>>1, k;
for (;i<n-1;i++) {
if (i < j) swap(a[i],a[j]);
for (k=n>>1;j>=k;) {j -= k; k >>= 1;}
if (j < k) j += k;
}
}
inline void NTT(int *f,int ldn,int is) {
int n = (1<<ldn);
revbin_permute(f,n);
for (int i=0;i<n;i+=2) {
int tmp1 = f[i], tmp2 = f[i+1];
f[i] = add(tmp1,tmp2), f[i+1] = sub(tmp1,tmp2);
}
for (int ldm=2;ldm<=ldn;ldm++) {
int m = (1<<ldm), mh = (m>>1);
int dw = is>0?wn[ldm]:iwn[ldm], w = 1;
for (int j=0;j<mh;j++) {
for (int r=0;r<n;r+=m) {
int u = f[r+j], v = mul(f[r+j+mh],w);
f[r+j] = add(u,v);
f[r+j+mh] = sub(u,v);
}
w = mul(w,dw);
}
}
}
//多項式乘法
inline void convolution(int *f,int *g,int n) {
int ldn; for (int i=20;i>=0;i--) if (n&(1<<i)) {ldn=i;break;}
NTT(f,ldn,1); NTT(g,ldn,1); //會改變g
for (int i=0;i<n;i++) f[i] = mul(f[i],g[i]);
NTT(f,ldn,-1);
int iv = qpow(n,mod-2);
for (int i=0;i<n;i++) f[i] = mul(f[i],iv);
}
//多項式求sq
inline void polysq(int *f,int n) {
int ldn; for (int i=20;i>=0;i--) if (n&(1<<i)) {ldn=i;break;}
NTT(f,ldn,1);
for (int i=0;i<n;i++) f[i] = mul(f[i],f[i]);
NTT(f,ldn,-1);
int iv = qpow(n,mod-2);
for (int i=0;i<n;i++) f[i] = mul(f[i],iv);
}
//多項式求inv
//Q(2n) = Q(n) - P*Q^2(n)
inline void polyinv(int *f,int n) {
static int g[N],b[N],c[N];
for (int i=0;i<n;i++) g[i]=0;
g[0] = qpow(f[0],mod-2);
for (int i=2;i<=n;i<<=1) {
for (int j=0;j<i;j++) b[j] = g[j], c[j] = f[j];
for (int j=i;j<2*i;j++) b[j] = c[j] = 0;
polysq(b,2*i);
for (int j=i;j<2*i;j++) b[j] = 0;
convolution(b,c,2*i);
for (int j=0;j<i;j++) g[j] = (2ll*g[j] - b[j] + mod)%mod;
}
for (int i=0;i<n;i++) f[i] = g[i];
}
//多項式求sqrt
//R(2n) = 1/2 * (R(n)+P(n)*R^{-1}(n))
inline void polysqrt(int *f,int n) {
static int g[N],b[N],c[N];
g[0] = 1; //根據需要改為sqrt(f[0])
for (int i=2;i<=n;i<<=1) {
for (int j=0;j<i;j++) b[j] = f[j], c[j] = g[j];
for (int j=i;j<2*i;j++) b[j] = c[j] = 0;
polyinv(c,i);
convolution(b,c,2*i);
for (int j=0;j<i;j++) g[j] = (LL)modinv2*(g[j] + b[j]) % mod;
}
for (int i=0;i<n;i++) f[i] = g[i];
}
int main()
{
init(); int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
c[x]=mod-4;
}
int lg;
for(lg=1;lg<=m;lg<<=1);
c[0]++;polysqrt(c,lg);
c[0]++; polyinv(c,lg);
for(int i=1;i<=m;i++)
printf("%d\n",(LL)2*c[i]%mod);
return 0;
}