一.概念

LLE：Locally linear embedding(區域性線性嵌入演算法)是一種非線性降維演算法，它能夠使降維後的資料較好地保持原有流形結構。LLE可以說是流形學習方法最經典的工作之一。和傳統的PCA，LDA等關注樣本方差的降維方法相比，LLE關注於降維時保持樣本區域性的線性特徵，由於LLE在降維時保持了樣本的區域性特徵。

二.演算法

LLE演算法認為每一個數據點都可以由其近鄰點的線性加權組合構造得到。演算法的主要步驟分為三步：(1)尋找每個樣本點的k個近鄰點；（2）由每個樣本點的近鄰點計算出該樣本點的區域性重建權值矩陣；（3）由該樣本點的區域性重建權值矩陣和其近鄰點計算出該樣本點的輸出值。

三.sklearn提供的API

sklearn的manifold提供了LLE方法（LocallyLinearEmbedding）

主要引數：

 def __init__(self, n_neighbors=5, n_components=2, reg=1E-3,
                 eigen_solver='auto', tol=1E-6, max_iter=100,
                 method='standard', hessian_tol=1E-4, modified_tol=1E-12,
                 neighbors_algorithm='auto', random_state=None, n_jobs=1):
        self.n_neighbors = n_neighbors
        self.n_components = n_components
        self.reg = reg
        self.eigen_solver = eigen_solver
        self.tol = tol
        self.max_iter = max_iter
        self.method = method
        self.hessian_tol = hessian_tol
        self.modified_tol = modified_tol
        self.random_state = random_state
        self.neighbors_algorithm = neighbors_algorithm
        self.n_jobs = n_jobs
 

n_neighbors：即我們搜尋樣本的近鄰的個數，最重要的就是這個，預設是5。 n_neighbors個數越大，則建立樣本區域性關係的時間會越大，也就意味著演算法的複雜度會增加。當然n_neighbors個數越大，則降維後樣本的區域性關係會保持的更好。在下一節我們可以通過具體的例子看出這一點。一般來說，如果演算法執行時間可以接受，我們可以儘量選擇一個比較大一些的n_neighbors。
n_components：即我們降維到的維數。如果我們降維的目的是視覺化，則一般可以選擇2-5維。
reg ：正則化係數，在n_neighbors大於n_components時，即近鄰數大於降維的維數時，由於我們的樣本權重矩陣不是滿秩的，LLE通過正則化來解決這個問題。預設是0.001。一般不用管這個引數。當近鄰數遠遠的大於降維到的維數時可以考慮適當增大這個引數。
eigen_solver：特徵分解的方法。有‘arpack’和‘dense’兩者演算法選擇。當然也可以選擇'auto'讓scikit-learn自己選擇一個合適的演算法。‘arpack’和‘dense’的主要區別是‘dense’一般適合於非稀疏的矩陣分解。而‘arpack’雖然可以適應稀疏和非稀疏的矩陣分解，但在稀疏矩陣分解時會有更好演算法速度。當然由於它使用一些隨機思想，所以它的解可能不穩定，一般需要多選幾組隨機種子來嘗試。
method： 即LLE的具體演算法。LocallyLinearEmbedding支援4種LLE演算法，分別是'standard'對應我們標準的LLE演算法，'hessian'對應原理篇講到的HLLE演算法，'modified'對應原理篇講到的MLLE演算法，‘ltsa’對應原理篇講到的LTSA演算法。預設是'standard'。一般來說HLLE/MLLE/LTSA演算法在同樣的近鄰數n_neighbors情況下，執行時間會比標準的LLE長，當然降維的效果會稍微好一些。如果你對降維後的資料區域性效果很在意，那麼可以考慮使用HLLE/MLLE/LTSA或者增大n_neighbors，否則標準的LLE就可以了。需要注意的是使用MLLE要求n_neighbors > n_components，而使用HLLE要求n_neighbors > n_components * (n_components + 3) / 2
neighbors_algorithm：這個是k近鄰的搜尋方法，和KNN演算法的使用的搜尋方法一樣。演算法一共有三種，第一種是蠻力實現，第二種是KD樹實現，第三種是球樹實現。這三種方法在K近鄰法(KNN)原理小結中都有講述，如果不熟悉可以去複習下。對於這個引數，一共有4種可選輸入，‘brute’對應第一種蠻力實現，‘kd_tree’對應第二種KD樹實現，‘ball_tree’對應第三種的球樹實現， ‘auto’則會在上面三種演算法中做權衡，選擇一個擬合最好的最優演算法。需要注意的是，如果輸入樣本特徵是稀疏的時候，無論我們選擇哪種演算法，最後scikit-learn都會去用蠻力實現‘brute’。個人的經驗，如果樣本少特徵也少，使用預設的 ‘auto’就夠了。 如果資料量很大或者特徵也很多，用"auto"建樹時間會很長，效率不高，建議選擇KD樹實現‘kd_tree’，此時如果發現‘kd_tree’速度比較慢或者已經知道樣本分佈不是很均勻時，可以嘗試用‘ball_tree’。而如果輸入樣本是稀疏的，無論你選擇哪個演算法最後實際執行的都是‘brute’。

例項程式碼：瑞士捲

import numpy as np
import operator
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold
from itertools import cycle
from mpl_toolkits.mplot3d import Axes3D
def load_data():
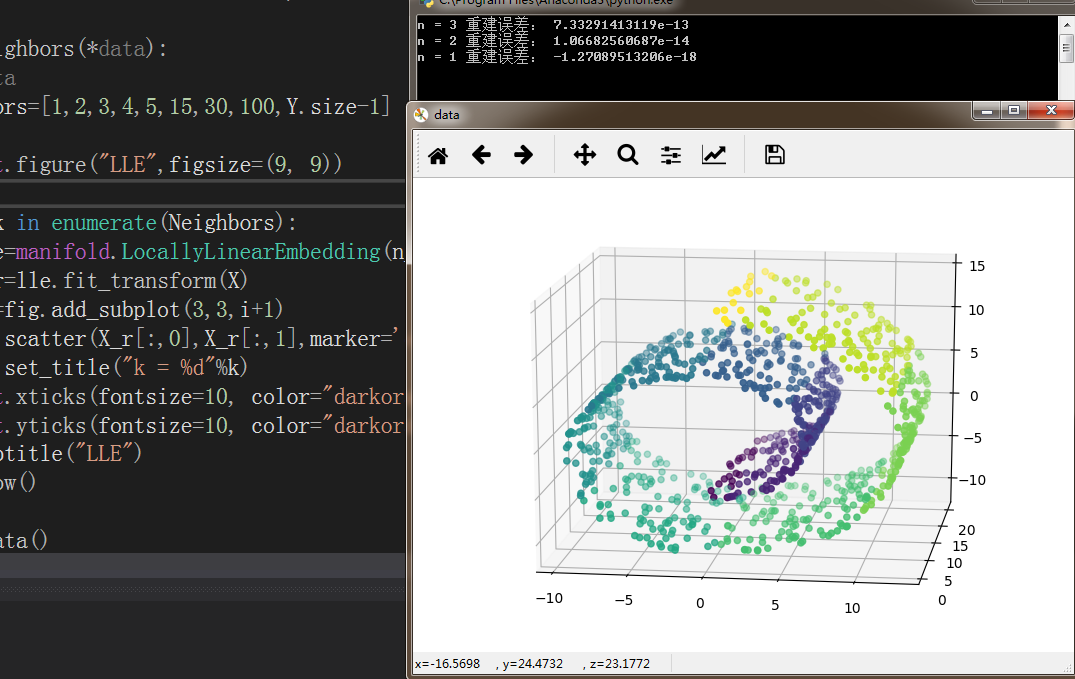
    swiss_roll =datasets.make_swiss_roll(n_samples=1000)
    return swiss_roll[0],np.floor(swiss_roll[1])

def LLE_components(*data):
    X,Y=data
    for n in [3,2,1]:
        lle=manifold.LocallyLinearEmbedding(n_components=n)
        lle.fit(X)
        print("n = %d 重建誤差："%n,lle.reconstruction_error_)

def LLE_neighbors(*data):
    X,Y=data
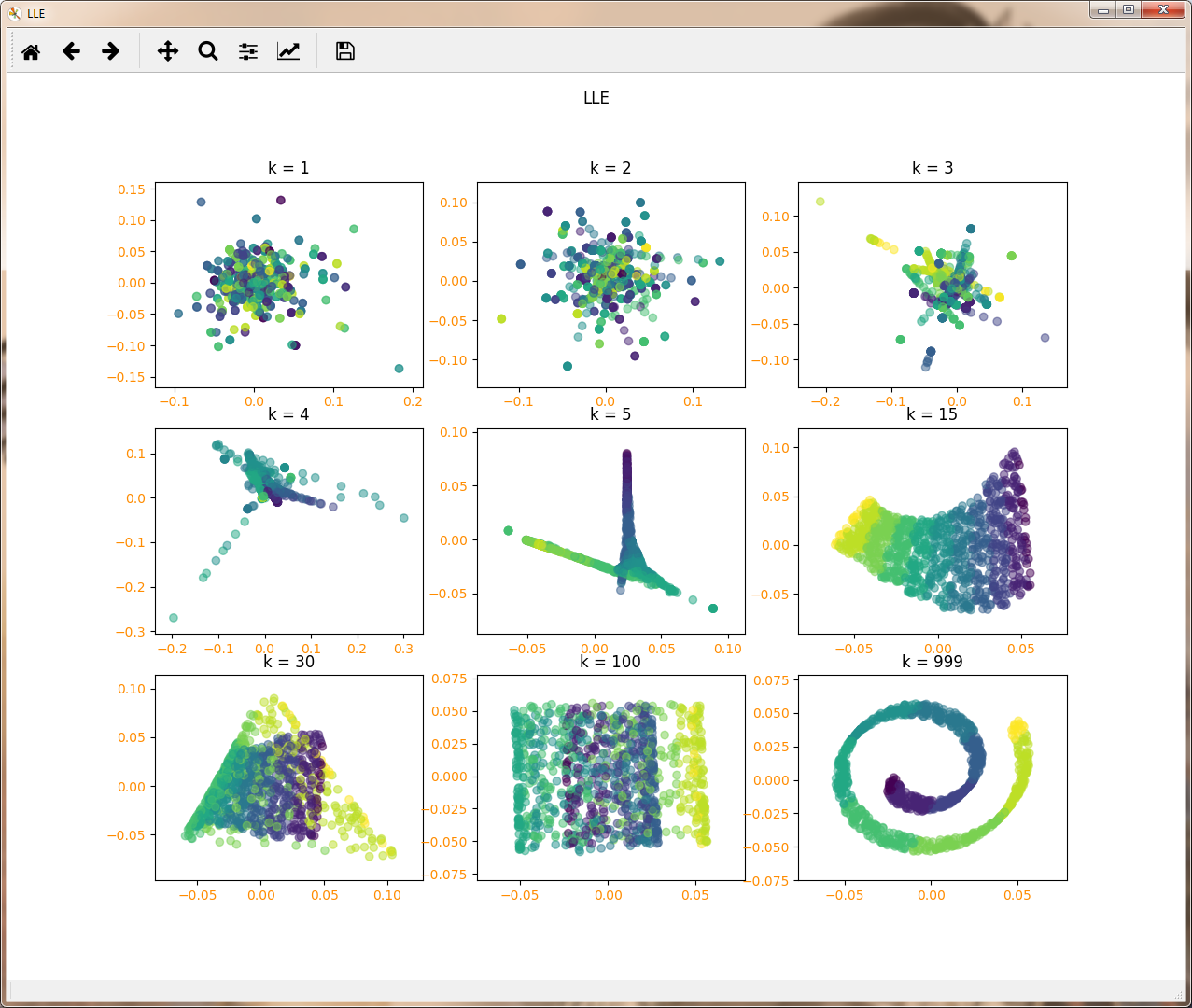
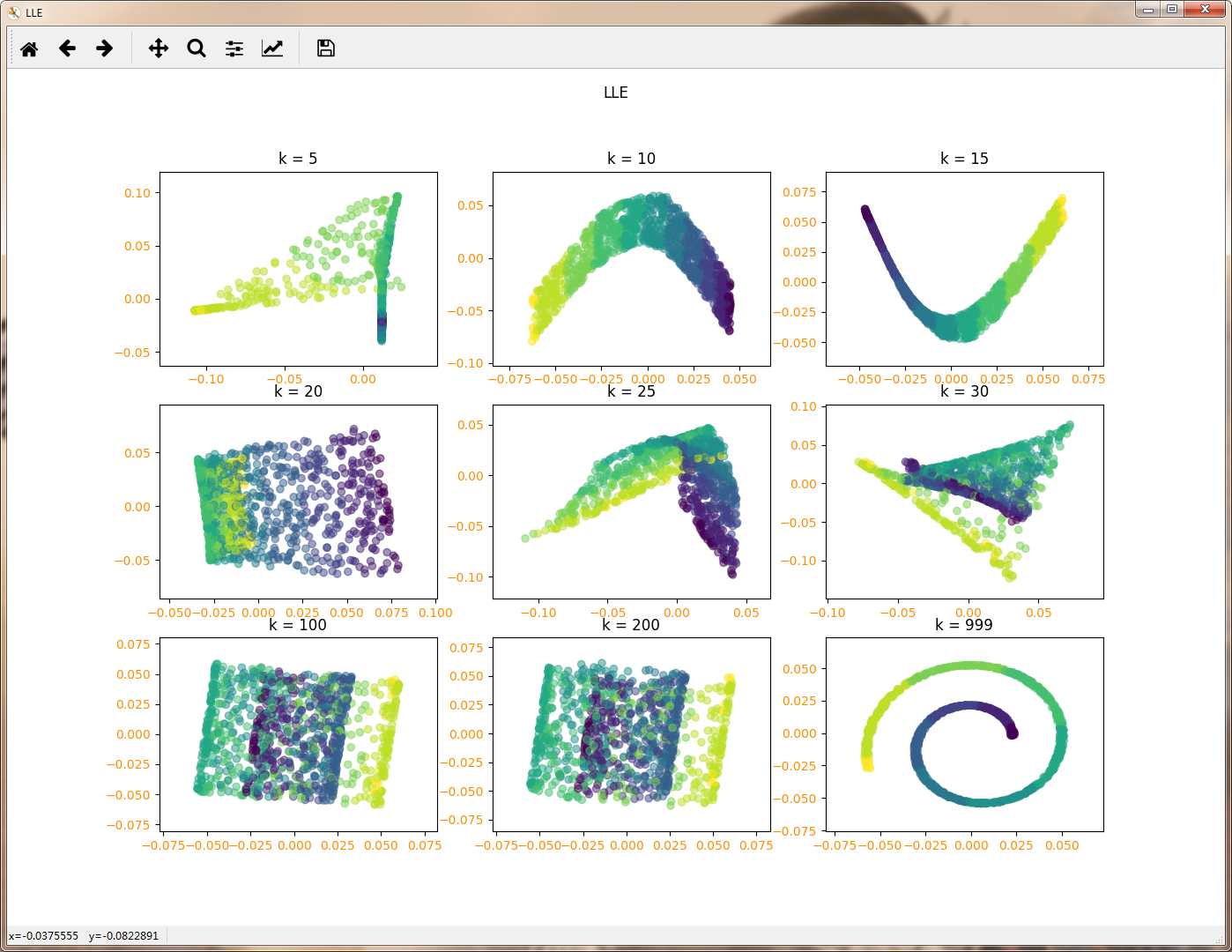
    Neighbors=[1,2,3,4,5,15,30,100,Y.size-1]

    fig=plt.figure("LLE",figsize=(9, 9))
  
    for i,k in enumerate(Neighbors):
        lle=manifold.LocallyLinearEmbedding(n_components=2,n_neighbors=k,eigen_solver='dense')
        X_r=lle.fit_transform(X)
        ax=fig.add_subplot(3,3,i+1)
        ax.scatter(X_r[:,0],X_r[:,1],marker='o',c=Y,alpha=0.5) 
        ax.set_title("k = %d"%k)   
        plt.xticks(fontsize=10, color="darkorange")  
        plt.yticks(fontsize=10, color="darkorange") 
    plt.suptitle("LLE")
    plt.show()

X,Y=load_data()
fig = plt.figure('data')
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o',c=Y)
LLE_components(X,Y)
LLE_neighbors(X,Y)

四.總結

LLE演算法計算複雜度相對較小，實現也算比較容易。且可以學習任意維的區域性線性的低維流形。但是對資料的流形分佈特徵有嚴格的要求。比如不能是閉合流形，不能是稀疏的資料集，不能是分佈不均勻的資料集等等。通過上述程式碼也能看出，演算法對最近鄰樣本數的選擇非常敏感，不同的最近鄰數對最後的降維結果有很大影響。

五.相關學習資源